このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
並列木複素数ウェーブレット変換
この例では、信号処理、イメージ処理およびボリューム処理での大きくサンプリングされている DWT に対する並列木複素数ウェーブレット変換 (DTCWT) の利点を示します。DTCWT は 2 つの別個の 2 チャネル フィルター バンクとして実装されます。この例で説明する利点を得るには、2 つのツリーで使用されるスケーリングおよびウェーブレット フィルターを任意に選択することはできません。一方のツリーのローパス (スケーリング) およびハイパス (ウェーブレット) フィルター は、他方のツリーのローパスおよびハイパス フィルター によって生成されたスケーリング関数およびウェーブレットの近似ヒルベルト変換である、スケーリング関数およびウェーブレットを生成しなければなりません。したがって、2 つのツリーから形成される複素数値のスケーリング関数およびウェーブレットはほぼ解析的です。
この結果、 次元データについての冗長性係数が のみである大きくサンプリングされた DWT と比較して、DTCWT はシフト変化が少なくなり、方向選択性が強くなります。DTCWT の冗長性は、非間引き (定常) DWT の冗長性よりも大幅に少なくなります。
この例では、DTCWT の近似シフト不変、ウェーブレットを 2 次元および 3 次元で解析する並列木の選択的方向、およびイメージとボリュームのノイズ除去における並列木複素数離散ウェーブレット変換の使用方法について説明します。
DTCWT の近接シフト不変
DWT はシフト変化の影響を受けます。つまり、入力信号またはイメージ内の小さなシフトが、DWT 係数のスケール全体における信号/イメージ エネルギーの分布に大きな変化を引き起こします。DTCWT はほぼシフト不変です。
これをテスト信号で示すには、2 つのシフト離散時間インパルスを 128 サンプルの長さで構築します。一方の信号には 60 番目のサンプルに単位インパルスがありますが、他方の信号には 64 番目のサンプルに単位インパルスがあります。両方の信号が単位エネルギー ( ノルム) をもつことは明確です。
kronDelta1 = zeros(128,1); kronDelta1(60) = 1; kronDelta2 = zeros(128,1); kronDelta2(64) = 1;
DWT 拡張モードを周期化として設定します。長さ 14 のウェーブレット フィルターおよびスケーリング フィルターを使用して 2 つの信号の DWT および DTCWT をレベル 3 まで下げて取得します。比較のためにレベル 3 の Detail 係数を抽出します。
origmode = dwtmode('status','nodisplay'); dwtmode('per','nodisp') J = 3; [dwt1C,dwt1L] = wavedec(kronDelta1,J,'sym7'); [dwt2C,dwt2L] = wavedec(kronDelta2,J,'sym7'); dwt1Cfs = detcoef(dwt1C,dwt1L,3); dwt2Cfs = detcoef(dwt2C,dwt2L,3); [dt1A,dt1D] = dualtree(kronDelta1,'Level',J,'FilterLength',14); [dt2A,dt2D] = dualtree(kronDelta2,'Level',J,'FilterLength',14); dt1Cfs = dt1D{3}; dt2Cfs = dt2D{3};
レベル 3 における 2 つの信号の DWT 係数および DTCWT 係数の絶対値をプロットし、係数のエネルギー (二乗した ノルム) を計算します。同じスケールで係数をプロットします。信号の 4 つのサンプル シフトにより、レベル 3 の DWT 係数のエネルギーに大きな変化が発生しています。レベル 3 の DTCWT 係数のエネルギーは、約 3% しか変化していません。
figure subplot(1,2,1) stem(abs(dwt1Cfs),'markerfacecolor',[0 0 1]) title({'DWT';['Squared 2-norm = ' num2str(norm(dwt1Cfs,2)^2,3)]},... 'fontsize',10) ylim([0 0.4]) subplot(1,2,2) stem(abs(dwt2Cfs),'markerfacecolor',[0 0 1]) title({'DWT';['Squared 2-norm = ' num2str(norm(dwt2Cfs,2)^2,3)]},... 'fontsize',10) ylim([0 0.4])

figure subplot(1,2,1) stem(abs(dt1Cfs),'markerfacecolor',[0 0 1]) title({'Dual-tree CWT';['Squared 2-norm = ' num2str(norm(dt1Cfs,2)^2,3)]},... 'fontsize',10) ylim([0 0.4]) subplot(1,2,2) stem(abs(dwt2Cfs),'markerfacecolor',[0 0 1]) title({'Dual-tree CWT';['Squared 2-norm = ' num2str(norm(dt2Cfs,2)^2,3)]},... 'fontsize',10) ylim([0 0.4])
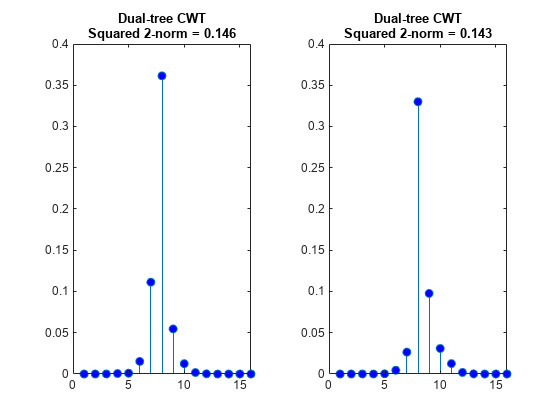
近似シフト不変の実用性を実際のデータで示すには、心電図 (ECG) 信号を解析します。ECG 信号のサンプリング間隔は 1/180 秒です。データは Percival & Walden [3] の p.125 から採用しています (元々ワシントン大学の William Constantine と Per Reinhall によって提供されたデータ)。便宜上、t=0 から始まるデータを採用しました。
load wecg dt = 1/180; t = 0:dt:(length(wecg)*dt)-dt; figure plot(t,wecg) xlabel('Seconds') ylabel('Millivolts')

約 0.7 秒離れている大きい正のピークは、心調律の R 波です。最初に、ほぼ対称的な Farras フィルターを使用して、大きくサンプリングされている DWT で信号を分解します。元の信号とレベル 2 およびレベル 3 のウェーブレット係数をプロットします。R 波が、与えられたサンプリング レートのこれらのスケールで最も著しく分離されているため、レベル 2 およびレベル 3 の係数が選択されました。
figure J = 6; [df,rf] = dtfilters('farras'); [dtDWT1,L1] = wavedec(wecg,J,df(:,1),df(:,2)); details = zeros(2048,3); details(2:4:end,2) = detcoef(dtDWT1,L1,2); details(4:8:end,3) = detcoef(dtDWT1,L1,3); subplot(3,1,1) stem(t,details(:,2),'Marker','none','ShowBaseline','off') title('Level 2') ylabel('mV') subplot(3,1,2) stem(t,details(:,3),'Marker','none','ShowBaseline','off') title('Level 3') ylabel('mV') subplot(3,1,3) plot(t,wecg) title('Original Signal') xlabel('Seconds') ylabel('mV')
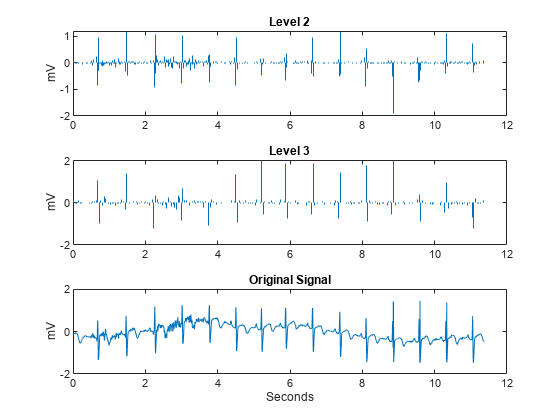
並列木変換について上記の解析を繰り返します。この場合、レベル 2 およびレベル 3 での並列木係数の実数部のプロットだけを行います。
[dtcplxA,dtcplxD] = dualtree(wecg,'Level',J,'FilterLength',14); details = zeros(2048,3); details(2:4:end,2) = dtcplxD{2}; details(4:8:end,3) = dtcplxD{3}; subplot(3,1,1) stem(t,real(details(:,2)),'Marker','none','ShowBaseline','off') title('Level 2') ylabel('mV') subplot(3,1,2) stem(t,real(details(:,3)),'Marker','none','ShowBaseline','off') title('Level 3') ylabel('mV') subplot(3,1,3) plot(t,wecg) title('Original Signal') xlabel('Seconds') ylabel('mV')

大きくサンプリングされているウェーブレット変換および並列木ウェーブレット変換の両方によって、同様のスケールに対する ECG の波形の重要な特徴の位置が特定されます。
1 次元信号におけるウェーブレットの重要な応用は、スケールによる分散分析を取得することです。この分散分析は入力信号の循環シフトの影響を受けるべきではないのは当然です。残念ながら、これは大きくサンプリングされている DWT には当てはまりません。これを示すには、ECG 信号を 4 サンプルずつ循環的にシフトして、大きくサンプリングされている DWT でシフトされていない信号とシフトされた信号を解析し、スケール全体のエネルギーの分布を計算します。
wecgShift = circshift(wecg,4); [dtDWT2,L2] = wavedec(wecgShift,J,df(:,1),df(:,2)); detCfs1 = detcoef(dtDWT1,L1,1:J,'cells'); apxCfs1 = appcoef(dtDWT1,L1,rf(:,1),rf(:,2),J); cfs1 = horzcat(detCfs1,{apxCfs1}); detCfs2 = detcoef(dtDWT2,L2,1:J,'cells'); apxCfs2 = appcoef(dtDWT2,L2,rf(:,1),rf(:,2),J); cfs2 = horzcat(detCfs2,{apxCfs2}); sigenrgy = norm(wecg,2)^2; enr1 = cell2mat(cellfun(@(x)(norm(x,2)^2/sigenrgy)*100,cfs1,'uni',0)); enr2 = cell2mat(cellfun(@(x)(norm(x,2)^2/sigenrgy)*100,cfs2,'uni',0)); levels = {'D1';'D2';'D3';'D4';'D5';'D6';'A6'}; enr1 = enr1(:); enr2 = enr2(:); table(levels,enr1,enr2,'VariableNames',{'Level','enr1','enr2'})
ans=7×3 table
Level enr1 enr2
______ ______ ______
{'D1'} 4.1994 4.1994
{'D2'} 8.425 8.425
{'D3'} 13.381 10.077
{'D4'} 7.0612 10.031
{'D5'} 5.4606 5.4436
{'D6'} 3.1273 3.4584
{'A6'} 58.345 58.366
元の信号とシフトされた信号の間のレベル 3 および 4 のウェーブレット係数によるエネルギーの変化は約 3% であることに注意してください。次に、並列木複素数離散ウェーブレット変換を使用してこの解析を繰り返します。
[dtcplx2A,dtcplx2D] = dualtree(wecgShift,'Level',J,'FilterLength',14); dtCfs1 = vertcat(dtcplxD,{dtcplxA}); dtCfs2 = vertcat(dtcplx2D,{dtcplx2A}); dtenr1 = cell2mat(cellfun(@(x)(norm(x,2)^2/sigenrgy)*100,dtCfs1,'uni',0)); dtenr2 = cell2mat(cellfun(@(x)(norm(x,2)^2/sigenrgy)*100,dtCfs2,'uni',0)); dtenr1 = dtenr1(:); dtenr2 = dtenr2(:); table(levels,dtenr1,dtenr2, 'VariableNames',{'Level','dtenr1','dtenr2'})
ans=7×3 table
Level dtenr1 dtenr2
______ ______ ______
{'D1'} 5.3533 5.3619
{'D2'} 6.2672 6.2763
{'D3'} 12.155 12.19
{'D4'} 8.2831 8.325
{'D5'} 5.81 5.8577
{'D6'} 3.1768 3.0526
{'A6'} 58.403 58.384
並列木変換により、元の信号およびその循環的にシフトされた信号のスケールによる一貫した分散分析が得られます。
イメージ処理における方向選択性
2 次元における DWT の標準実装では、イメージの列と行の分割可能なフィルター処理を使用します。補助関数 helperPlotCritSampDWT を使用して、4 つの消失モーメントを持つ Daubechies の最小非対称位相ウェーブレット sym4 の LH、HL、HH ウェーブレットをプロットします。
helperPlotCritSampDWT

LH および HL ウェーブレットにはそれぞれ明確な水平方向および垂直方向があることに注意してください。ただし、右端の HH ウェーブレットは +45 および -45 度の両方の方向を混合して、チェッカーボードのアーティファクトを生成します。この方向の混合は、実数値の分割可能なフィルターの使用によるものです。HH の実数値の分割可能なフィルターには、2 次元周波数平面における高周波数の 4 つの隅すべてに通過帯域があります。
並列木 DWT は、ほぼ解析的である (つまり周波数軸の半分のみをサポートしている) ウェーブレットを使用して方向選択性を実現します。並列木 DWT では、実数部と虚数部の両方に 6 つのサブバンドがあります。6 つの実数部は、2 つのツリーに、列フィルター処理の出力の後に入力イメージの行フィルター処理の出力を追加することで形成されます。6 つの虚数部は、列フィルター処理の出力の後に行フィルター処理の出力を引くことで形成されます。
列と行に適用されるフィルターは、同じフィルターのペア ( または ) にすることも、異なるフィルターのペア () にすることもできます。補助関数 helperPlotWaveletDTCWT を使用して、DTCWT の実数部と虚数部に対応する 12 のウェーブレットの方向をプロットします。この図の最初の行は 6 つのウェーブレットの実数部を示し、2 行目は虚数部を示します。
helperPlotWaveletDTCWT

2 次元でのエッジ表現
複素数並列木ウェーブレットの近似解析および選択的配向により、イメージ内のエッジの表現において、2 次元の標準 DWT より優れたパフォーマンスが得られます。これを説明するために、大きくサンプリングされている 2 次元の DWT および 2 次元の複素数方向の並列木変換を使用して、複数方向の直線および曲線の特異点から構成されるエッジをもつテスト イメージを解析します。最初に、線の特異点から構成される八角形のイメージを解析します。
load woctagon imagesc(woctagon) colormap gray title('Original Image') axis equal axis off

補助関数 helprPlotOctagon を使用してイメージをレベル 4 まで分解し、レベル 4 の Detail 係数に基づいてイメージの Approximation を再構築します。
helperPlotOctagon(woctagon)

次に、双曲線エッジをもつ八角形を解析します。双曲線八角形のエッジは曲線の特異点です。
load woctagonHyperbolic figure imagesc(woctagonHyperbolic) colormap gray title('Octagon with Hyperbolic Edges') axis equal axis off

再び、補助関数 helprPlotOctagon を使用してイメージをレベル 4 まで分解し、2 次元の標準 DWT および複素数方向の並列木 DWT の両方についてレベル 4 の Detail 係数に基づいてイメージの Approximation を再構築します。
helperPlotOctagon(woctagonHyperbolic)

2 次元の大きくサンプリングされている DWT で明確なリンギング アーティファクトが、両方のイメージの 2 次元の DTCWT にはないことがわかります。DTCWT は、線および曲線の特異点をより忠実に再現します。
イメージのノイズ除去
別個のサブバンド内の異なる方向を分離する機能のため、DTCWT はイメージのノイズ除去などの応用において標準の分離可能な DWT より性能が優れていることがよくあります。これを示すために、補助関数 helperCompare2DDenoisingDTCWT を使用します。補助関数はイメージを読み込み、 であるゼロ平均のホワイト ガウス ノイズを加えます。ユーザー指定のしきい値の範囲について、この関数は、大きくサンプリングされている DWT、および DTCWT のソフトなしきい値処理を使用したノイズ除去を比較します。各しきい値について、平方根平均二乗 (RMS) 誤差およびピーク S/N 比 (PSNR) が表示されます。
numex = 3;
helperCompare2DDenoisingDTCWT(numex,0:2:100,'PlotMetrics');

DTCWT の性能は、RMS 誤差および PSNR で標準の DWT より優れています。
次に、加法性ノイズの標準偏差と等しい、しきい値 25 のノイズ除去後のイメージを取得します。
numex = 3;
helperCompare2DDenoisingDTCWT(numex,25,'PlotImage');
加法性ノイズの標準偏差と等しいしきい値では、DTCWT が 2 次元の標準 DWT より約 4 dB 高い PSNR を提供します。
3 次元での方向選択性
2 次元の分離可能な DWT で見られるリンギング アーティファクトは、ウェーブレット解析をさらに高い次元に拡張すると悪化します。DTCWT により、最小限の冗長性で 3 次元の方向選択性を維持できます。3 次元では、並列木変換には 28 のウェーブレット サブバンドがあります。
3 次元の並列木ウェーブレット変換の方向選択性を示すため、3 次元並列木および分離可能な DWT ウェーブレットの両方について 3 次元等値面の例を可視化します。最初に、2 つの並列木サブバンドの実数部と虚数部を別個に可視化します。
helperVisualize3D('Dual-Tree',28,'separate')

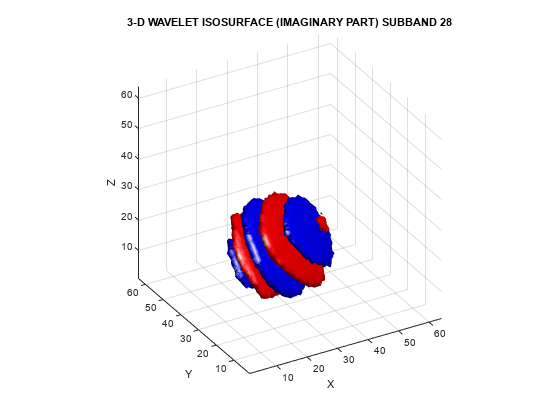
helperVisualize3D('Dual-Tree',25,'separate')
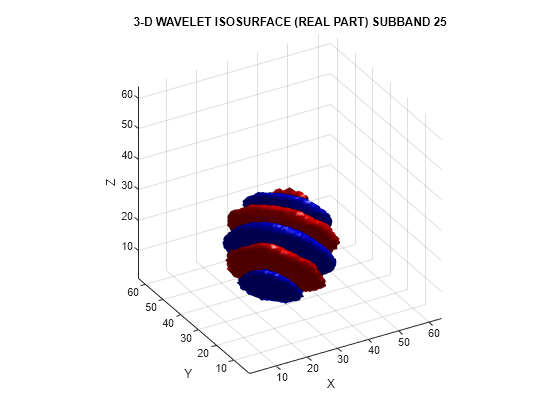

等値面プロットの赤い部分は、ウェーブレットのゼロから正の偏位を示し、青い部分は負の偏位を表します。並列木ウェーブレットの実数部と虚数部の空間の方向選択性をはっきりと確認できます。次に、実数部と虚数部のプロットが 1 つの等値面としてまとめてプロットされている並列木サブバンドの 1 つを可視化します。
helperVisualize3D('Dual-Tree',25,'real-imaginary')

前のプロットは、実数部と虚数部が空間内でそれぞれシフトされたものを示します。これは、複素数ウェーブレットの虚数部が実数部の近似ヒルベルト変換であるという事実を反映しています。次に、比較のため、実数の直交ウェーブレットの等値面を 3 次元で可視化します。
helperVisualize3D('DWT',7)
2 次元 DWT で見られる方向の混合は、3 次元ではより顕著になります。2 次元の場合と同様に、3 次元での方向の混合は大幅なリンギングまたはブロッキング アーティファクトを引き起こします。これを示すために、球状ボリュームについて 3 次元の DWT および DTCWT ウェーブレットの Detail を調べます。球体は 64 × 64 × 64 です。
load sphr [A,D] = dualtree3(sphr,2,'excludeL1'); A = zeros(size(A)); sphrDTCWT = idualtree3(A,D); montage(reshape(sphrDTCWT,[64 64 1 64]),'DisplayRange',[]) title('DTCWT Level 2 Details')

分離可能な DWT に基づいて前のプロットと第 2 レベルの Detail を比較します。
sphrDEC = wavedec3(sphr,2,'sym4','mode','per'); sphrDEC.dec{1} = zeros(size(sphrDEC.dec{1})); for kk = 2:8 sphrDEC.dec{kk} = zeros(size(sphrDEC.dec{kk})); end sphrrecDWT = waverec3(sphrDEC); figure montage(reshape(sphrrecDWT,[64 64 1 64]),'DisplayRange',[]) title('DWT Level 2 Details')

DTCWT および DWT モンタージュの両方のイメージを拡大すると、DTCWT と比較して DWT の Detail のブロッキング アーティファクトがどれほど顕著かがわかります。
ボリュームのノイズ除去
2 次元の場合と同様に、3 次元の DTCWT の方向選択性は多くの場合にボリュームのノイズ除去を改善します。
これを示すために、16 スライスで構成される MRI データセットについて考えます。標準偏差 10 のガウス ノイズは元のデータセットに付加されています。ノイズを含むデータセットを表示します。
load MRI3D montage(reshape(noisyMRI,[128 128 1 16]),'DisplayRange',[])
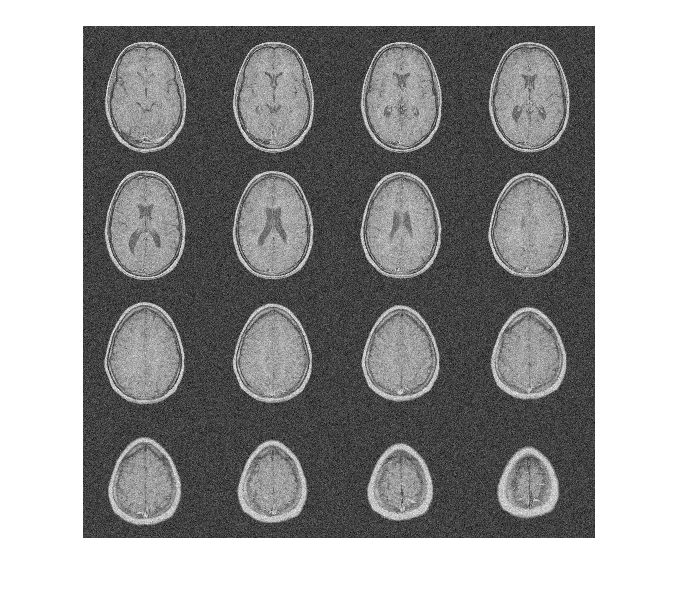
ノイズ除去前の元の SNR は約 11 dB です。
20*log10(norm(origMRI(:),2)/norm(origMRI(:)-noisyMRI(:),2))
ans = 11.2997
DTCWT および DWT の両方を使用して、レベル 4 まで下げて MRI データセットのノイズを除去します。同様のウェーブレット フィルター長は両方の場合に使用されます。しきい値の関数として結果の SNR をプロットします。最適な SNR で取得された DTCWT および DWT の両方についてノイズ除去された結果を表示します。
[imrecDTCWT,imrecDWT] = helperCompare3DDenoising(origMRI,noisyMRI);
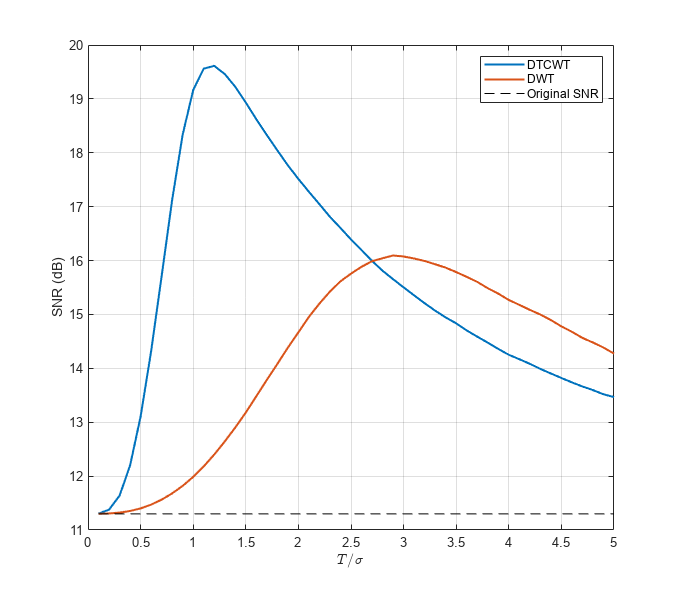
figure montage(reshape(imrecDTCWT,[128 128 1 16]),'DisplayRange',[]) title('DTCWT Denoised Volume')

figure montage(reshape(imrecDWT,[128 128 1 16]),'DisplayRange',[]) title('DWT Denoised Volume')

拡張モードを元に戻します。
dwtmode(origmode,'nodisplay')まとめ
並列木 CWT には、大きくサンプリングされている DWT で達成不可能な近接シフト不変および方向選択性の望ましい性質があることを示しました。これらの性質による信号解析のパフォーマンスの向上、イメージとボリューム内でのエッジの表現、およびイメージとボリュームのノイズ除去について説明しました。
参考文献
Huizhong Chen, and N. Kingsbury.“Efficient Registration of Nonrigid 3-D Bodies.”IEEE Transactions on Image Processing 21, no. 1 (January 2012):262–72. https://doi.org/10.1109/TIP.2011.2160958.
Kingsbury, Nick.“Complex Wavelets for Shift Invariant Analysis and Filtering of Signals.”Applied and Computational Harmonic Analysis 10, no. 3 (May 2001):234–53. https://doi.org/10.1006/acha.2000.0343.
Percival, Donald B., and Andrew T. Walden.Wavelet Methods for Time Series Analysis.Cambridge Series in Statistical and Probabilistic Mathematics.Cambridge ; New York:Cambridge University Press, 2000.
Selesnick, I.W., R.G. Baraniuk, and N.C. Kingsbury.“The Dual-Tree Complex Wavelet Transform.”IEEE Signal Processing Magazine 22, no. 6 (November 2005):123–51. https://doi.org/10.1109/MSP.2005.1550194.
Selesnick, I."The Double Density DWT."Wavelets in Signal and Image Analysis:From Theory to Practice (A. A. Petrosian, and F. G. Meyer, eds.).Norwell, MA:Kluwer Academic Publishers, 2001, pp. 39–66.
Selesnick, I.W.“The Double-Density Dual-Tree DWT.”IEEE Transactions on Signal Processing 52, no. 5 (May 2004):1304–14. https://doi.org/10.1109/TSP.2004.826174.
参考
dualtree | dualtree2 | dualtree3
