Padé Approximant of Time-Delay Input
This example shows how to use a Padé approximant in control system theory to model time delays in the response of a first-order system. Time delays arise in systems such as chemical and transport processes where there is a delay between the input and the system response. When these inputs are modeled, they are called dead-time inputs.
This example uses Symbolic Math Toolbox™ to solve for the transfer function of a first-order system and find the system response to dead-time step input using Padé approximant. This example performs calculations symbolically to obtain analytic results.
Introduction
The Padé approximant of order [m, n] approximates the function f(x) around as
The Padé approximant is a rational function formed by a ratio of two power series. Because it is a rational function, it is more accurate than the Taylor series in approximating functions with poles. The Padé approximant is represented by the Symbolic Math Toolbox™ function pade.
When a pole or zero exists at the expansion point , the accuracy of the Padé approximant decreases. To increase accuracy, use an alternative form of the Padé approximant which is
The pade function returns the alternative form of the Padé approximant when you set the OrderMode input argument to Relative.
Find Transfer Function of First-Order System
The behavior of a first-order system is described by this differential equation
Enter the differential equation in MATLAB®.
syms tau a x(t) y(t) xS(s) yS(s) H(s) tmp F = tau*diff(y)+y == a*x;
Find the Laplace transform of F using laplace.
F = laplace(F,t,s)
F =
Assume the response of the system at t = 0 is 0. Use subs to substitute for y(0) = 0.
F = subs(F,y(0),0)
F =
To collect common terms, use simplify.
F = simplify(F)
F =
For readability, replace the Laplace transforms of x(t) and y(t) with xS(s) and yS(s).
F = subs(F,[laplace(x(t),t,s) laplace(y(t),t,s)],[xS(s) yS(s)])
F =
The Laplace transform of the transfer function is yS(s)/xS(s). Divide both sides of the equation by xS(s) and use subs to replace yS(s)/xS(s) with H(s).
F = F/xS(s); F = subs(F,yS(s)/xS(s),H(s))
F =
Solve the equation for H(s). Substitute for H(s) with a dummy variable, solve for the dummy variable using solve, and assign the solution to Hsol(s).
F = subs(F,H(s),tmp); Hsol(s) = solve(F,tmp)
Hsol(s) =
Find Response of System to Time-Delayed Step Input
The input to the first-order system is a time-delayed step input. To represent a step input, use heaviside. Delay the input by three time units. Find the Laplace transform using laplace.
step = heaviside(t - 3); step = laplace(step)
step =
Find the response of the system, which is the product of the transfer function and the input.
y = Hsol(s)*step
y =
To allow plotting of the response, set parameters a and tau to specific values. For a and tau, choose values 1 and 3, respectively.
y = subs(y,[a tau],[1 3]); y = ilaplace(y,s);
Find Response of System Using Padé Approximants
Find the Padé approximant of order [2 2] of the step input using the Order input argument to pade.
stepPade22 = pade(step,'Order',[2 2])stepPade22 =
Find the response to the input by multiplying the transfer function and the Padé approximant of the input.
yPade22 = Hsol(s)*stepPade22
yPade22 =
Find the inverse Laplace transform of yPade22 using ilaplace.
yPade22 = ilaplace(yPade22,s)
yPade22 =
To plot the response, set parameters a and tau to their values of 1 and 3, respectively.
yPade22 = subs(yPade22,[a tau],[1 3])
yPade22 =
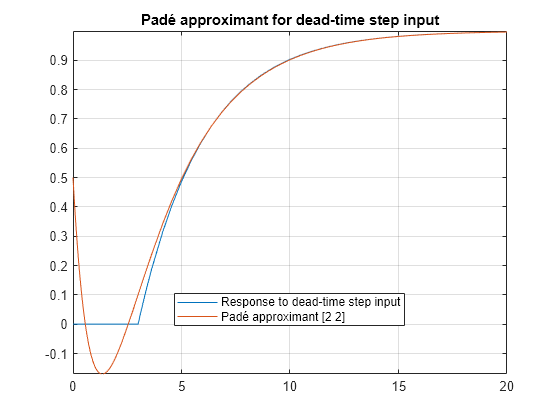
Plot the response of the system y and the response calculated from the Padé approximant yPade22.
fplot(y,[0 20]) hold on fplot(yPade22, [0 20]) grid on title 'Padé approximant for dead-time step input' legend('Response to dead-time step input', 'Padé approximant [2 2]',... 'Location', 'Best');
Increase Accuracy of Padé Approximant Using OrderMode
The [2 2] Padé approximant does not represent the response well because a pole exists at the expansion point of 0. To increase the accuracy of pade when there is a pole or zero at the expansion point, set the OrderMode input argument to Relative and repeat the steps. For details, see pade.
stepPade22Rel = pade(step,'Order',[2 2],'OrderMode','Relative')
stepPade22Rel =
yPade22Rel = Hsol(s)*stepPade22Rel
yPade22Rel =
yPade22Rel = ilaplace(yPade22Rel); yPade22Rel = subs(yPade22Rel,[a tau],[1 3])
yPade22Rel =
fplot(yPade22Rel, [0 20], 'DisplayName', 'Relative Padé approximant [2 2]')

Increase Accuracy of Padé Approximant by Increasing Order
You can increase the accuracy of the Padé approximant by increasing its order. Increase the order to [4 5] and repeat the steps. The [n-1 n] Padé approximant is better at approximating the response at t = 0 than the [n n] Padé approximant.
stepPade45 = pade(step,'Order',[4 5])stepPade45 =
yPade45 = Hsol(s)*stepPade45
yPade45 =
yPade45 = subs(yPade45,[a tau],[1 3])
yPade45 =
Find the inverse Laplace transform of yPade45 using ilaplace. Approximate yPade45 numerically using vpa. Plot the response calculated from the Padé approximant yPade45.
yPade45 = vpa(ilaplace(yPade45)); fplot(yPade45, [0 20], 'DisplayName', 'Padé approximant [4 5]')

Conclusions
The following points have been shown:
Padé approximants can model dead-time step inputs.
The accuracy of the Padé approximant increases with the increase in the order of the approximant.
When a pole or zero exists at the expansion point, the Padé approximant is inaccurate about the expansion point. To increase the accuracy of the approximant, set the
OrderModeoption toRelative. You can also use increase the order of the denominator relative to the numerator.
