このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
方程式の解法
代数方程式および微分方程式の求解
代数方程式、微分方程式および微分代数方程式 (DAE) を解くことができます。
代数方程式を解き、厳密な解析解または高精度の数値解を求めます。解析解には solve、数値解には vpasolve を使用します。線形方程式を解くには、linsolve を使用します。これらのソルバー関数には、複雑な問題を扱う柔軟性があります。関数 solve で求めた方程式の解のトラブルシューティングを参照してください。
微分方程式を解くには、dsolve を使用します。これらの微分方程式は、シンボリック関数を使用して作成します。シンボリック関数の作成を参照してください。
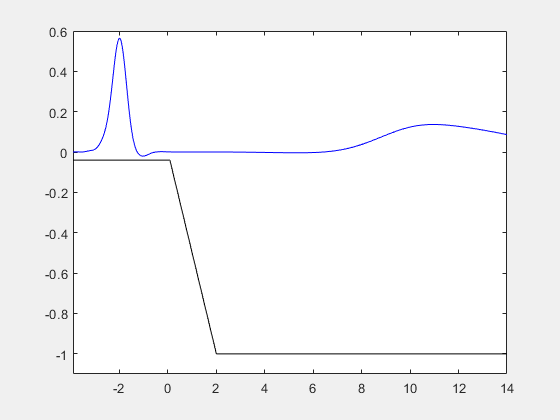
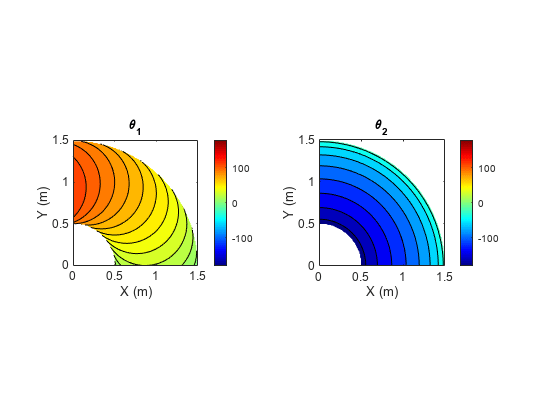
微分代数方程式 (DAE) を解くには、最初に Symbolic Math Toolbox™ 関数を使用して微分指数を 1 または 0 に簡約した後、ode15i、ode15s、ode23t などの MATLAB® ソルバーを使用します。微分代数方程式 (DAE) の求解を参照してください。
ライブ エディター タスク
| 求解 (シンボリック式) | ライブ エディターでシンボリック方程式の解析解を求める (R2020a 以降) |
関数
トピック
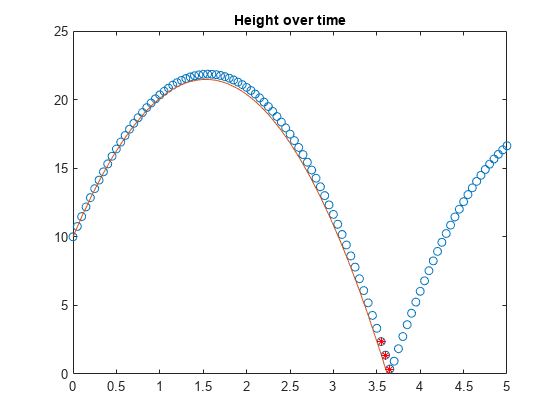
- 代数方程式の求解
方程式を解析的に解き、完全解を返した後、結果を可視化します。
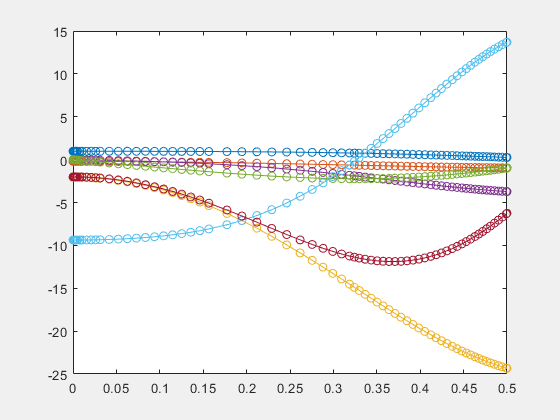
- 微分方程式の求解
関数
dsolveを使用して微分方程式を解析的に解きます。 - 微分代数方程式 (DAE) の求解
この例では、MATLAB® と Symbolic Math Toolbox™ を使用して微分代数方程式 (DAE) を解く方法を示します。