このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

kmeans

k-means クラスタリング

構文

idx = kmeans(X,k)

idx = kmeans(X,k,Name,Value)

[idx,C] = kmeans(___)

[idx,C,sumd] = kmeans(___)

[idx,C,sumd,D] = kmeans(___)

説明

idx = kmeans(X,k) は k-means クラスタリングを実行して n 行 p 列のデータ行列 X の観測を k クラスターに分割し、観測ごとにクラスター インデックスを含む n 行 1 列のベクトル (idx) を返します。X の行は観測に対応し、列は変数に対応します。

既定の設定では、kmeans はクラスター中心の初期化に二乗ユークリッド距離計量と k-means++ アルゴリズムを使用します。

idx = kmeans(X,k,Name,Value) は、1 つ以上の Name,Value のペア引数により指定された追加オプションを使用しクラスター インデックスを返します。

たとえば、コサイン距離、新たな初期値を使用するクラスタリングの反復回数または並列計算の使用回数を指定します。

[idx,C] = kmeans(___) は、k 個のクラスター重心位置を k 行 p 列の行列 C に返します。

[idx,C,sumd] = kmeans(___) は、点と重心間距離のクラスター内合計を k 行 1 列のベクトル sumd で返します。

[idx,C,sumd,D] = kmeans(___) は、各点からすべての重心までの距離を n 行 k 列の行列 D で返します。

例

k-means クラスタリング アルゴリズムの学習

k-means クラスタリングを使用してデータをクラスター化し、クラスター領域をプロットします。

フィッシャーのアヤメのデータセットを読み込みます。花弁の長さと幅を予測子として使用します。

load fisheriris
X = meas(:,3:4);

figure;
plot(X(:,1),X(:,2),'k*','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)'; 
ylabel 'Petal Widths (cm)';

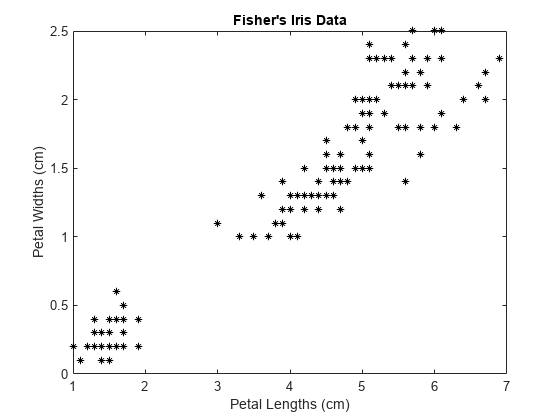
大きいクラスターは、分散がより低い領域とより高い領域に分割されているように見えます。つまり、大きなクラスターは、2 つのクラスターがオーバーラップしている可能性があります。

データをクラスタリングします。k = 3 クラスターを指定します。

rng(1); % For reproducibility
[idx,C] = kmeans(X,3);

idx は、X に含まれている観測値に対応する、予測したクラスターのインデックスのベクトルです。C は、最終的な重心位置が格納される 3 行 2 列の行列です。

kmeans を使用して各重心からグリッド上の点までの距離を計算します。これを行うには、重心 (C) およびグリッド上の点を kmeans へ渡し、そのアルゴリズムの 1 反復を実装します。

x1 = min(X(:,1)):0.01:max(X(:,1));
x2 = min(X(:,2)):0.01:max(X(:,2));
[x1G,x2G] = meshgrid(x1,x2);
XGrid = [x1G(:),x2G(:)]; % Defines a fine grid on the plot

idx2Region = kmeans(XGrid,3,'MaxIter',1,'Start',C);

Warning: Failed to converge in 1 iterations.

    % Assigns each node in the grid to the closest centroid

kmeans は、アルゴリズムが収束しないことを示す警告を表示します。これは、反復が 1 回のみ実行されることから予想できます。

クラスターの領域をプロットします。

figure;
gscatter(XGrid(:,1),XGrid(:,2),idx2Region,...
    [0,0.75,0.75;0.75,0,0.75;0.75,0.75,0],'..');
hold on;
plot(X(:,1),X(:,2),'k*','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)';
ylabel 'Petal Widths (cm)'; 
legend('Region 1','Region 2','Region 3','Data','Location','SouthEast');
hold off;

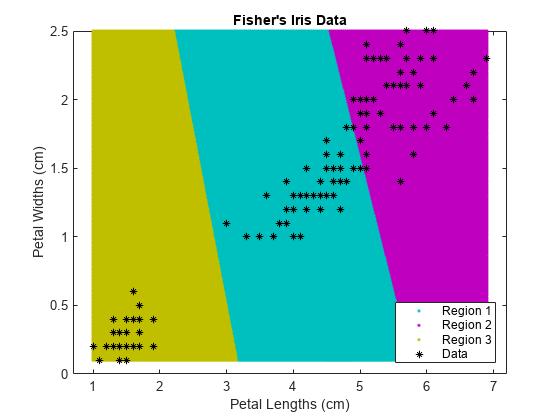
2 つのクラスターにデータを分割

標本データを無作為に生成します。

rng default; % For reproducibility
X = [randn(100,2)*0.75+ones(100,2);
    randn(100,2)*0.5-ones(100,2)];

figure;
plot(X(:,1),X(:,2),'.');
title 'Randomly Generated Data';

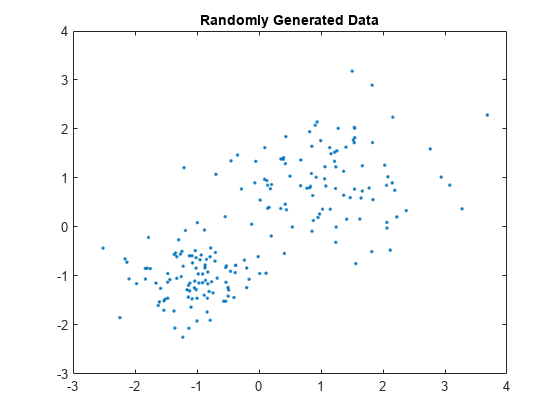
データ内に 2 つのクラスターが存在するように見えます。

データを 2 つのクラスターに分割し、5 つの初期値から最適な割り当てを選択します。最終出力を表示します。

opts = statset('Display','final');
[idx,C] = kmeans(X,2,'Distance','cityblock',...
    'Replicates',5,'Options',opts);

Replicate 1, 3 iterations, total sum of distances = 201.533.
Replicate 2, 5 iterations, total sum of distances = 201.533.
Replicate 3, 3 iterations, total sum of distances = 201.533.
Replicate 4, 3 iterations, total sum of distances = 201.533.
Replicate 5, 2 iterations, total sum of distances = 201.533.
Best total sum of distances = 201.533

既定では、k-means++ を使用して複製が個別に初期化されます。

クラスターとクラスター重心をプロットします。

figure;
plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12)
hold on
plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12)
plot(C(:,1),C(:,2),'kx',...
     'MarkerSize',15,'LineWidth',3) 
legend('Cluster 1','Cluster 2','Centroids',...
       'Location','NW')
title 'Cluster Assignments and Centroids'
hold off

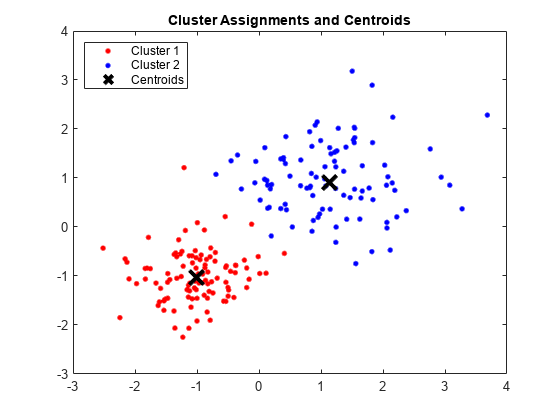
idx をsilhouetteへ渡すことで、クラスターがどの程度適切に分離されたかを判断できます。

並列計算を使用するクラスター データ

大きなデータセットのクラスタリングでは、特にオンライン更新 (既定で設定されている) を使用すると時間がかかる場合があります。Parallel Computing Toolbox™ のライセンスがある場合に並列計算のオプションを設定すると、kmeans は各クラスタリング タスク (または複製) を並列的に実行します。さらに、Replicates > 1 である場合、並列計算により収束までの時間が短くなります。

混合ガウス モデルから大きなデータセットを無作為に生成します。

Mu = bsxfun(@times,ones(20,30),(1:20)'); % Gaussian mixture mean
rn30 = randn(30,30);
Sigma = rn30'*rn30; % Symmetric and positive-definite covariance
Mdl = gmdistribution(Mu,Sigma); % Define the Gaussian mixture distribution

rng(1); % For reproducibility
X = random(Mdl,10000);

Mdl は、20 個の成分をもつ 30 次元の gmdistribution モデルです。X は、Mdl から生成されたデータが含まれている 10000 行 30 列の行列です。

並列計算のオプションを指定します。

stream = RandStream('mlfg6331_64');  % Random number stream
options = statset('UseParallel',1,'UseSubstreams',1,...
    'Streams',stream);

RandStream の入力引数 'mlfg6331_64' は、乗法ラグ フィボナッチ発生器アルゴリズムを使用するよう指定します。options は、推定を制御するためのオプションを指定するフィールドをもつ構造体配列です。

k-means クラスタリングを使用してデータをクラスター化します。データに k = 20 個のクラスターがあることを指定し、反復回数を増やします。通常、目的関数には局所的最小値が含まれます。10 個の複製を指定して、より低い局所的最小値の検出に役立てます。

tic; % Start stopwatch timer
[idx,C,sumd,D] = kmeans(X,20,'Options',options,'MaxIter',10000,...
    'Display','final','Replicates',10);

Starting parallel pool (parpool) using the 'local' profile ...
connected to 6 workers.
Replicate 5, 72 iterations, total sum of distances = 7.73161e+06.
Replicate 1, 64 iterations, total sum of distances = 7.72988e+06.
Replicate 3, 68 iterations, total sum of distances = 7.72576e+06.
Replicate 4, 84 iterations, total sum of distances = 7.72696e+06.
Replicate 6, 82 iterations, total sum of distances = 7.73006e+06.
Replicate 7, 40 iterations, total sum of distances = 7.73451e+06.
Replicate 2, 194 iterations, total sum of distances = 7.72953e+06.
Replicate 9, 105 iterations, total sum of distances = 7.72064e+06.
Replicate 10, 125 iterations, total sum of distances = 7.72816e+06.
Replicate 8, 70 iterations, total sum of distances = 7.73188e+06.
Best total sum of distances = 7.72064e+06

toc % Terminate stopwatch timer

Elapsed time is 61.915955 seconds.

6 つのワーカーが利用可能であることがコマンド ウィンドウに示されます。ワーカーの数はシステムにより異なる場合があります。コマンド ウィンドウは、各複製の反復回数および最終的な目的関数値を表示します。複製 9 は距離の総和が最小なので、その結果が出力引数に含まれます。

既存クラスターへの新しいデータの割り当てと C/C++ コードの生成

kmeansは、k-means クラスタリングを実行して、データを k 個のクラスターに分割します。新しいデータセットをクラスター化するときに、kmeans を使用して、既存のデータと新しいデータが含まれる新しいクラスターを作成できます。関数 kmeans は C/C++ コード生成をサポートするので、学習データを受け入れてクラスター化の結果を返すコードを生成してから、コードをデバイスに展開できます。このワークフローでは学習データを渡さなければなりませんが、サイズが非常に大きい可能性があります。デバイスのメモリを節約するため、kmeans とpdist2をそれぞれ使用して、学習と予測を分離することができます。

kmeans を使用して MATLAB® でクラスターを作成し、生成されたコードで pdist2 を使用して新しいデータを既存のクラスターに割り当てます。コード生成用に、クラスターの重心位置と新しいデータセットを受け入れて最も近いクラスターのインデックスを返すエントリポイント関数を定義します。次に、エントリポイント関数のコードを生成します。

C/C++ コードの生成には MATLAB® Coder™ が必要です。

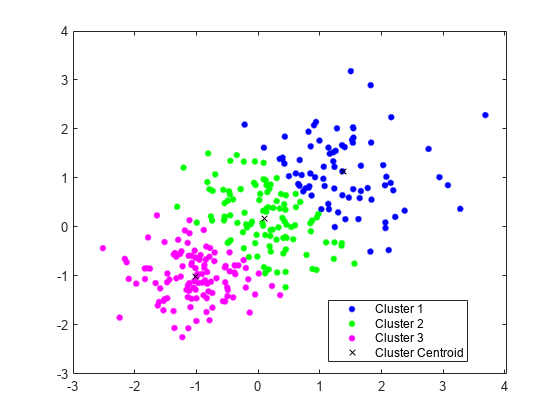
k-means クラスタリングの実行

3 つの分布を使用して、学習データセットを生成します。

rng('default') % For reproducibility
X = [randn(100,2)*0.75+ones(100,2);
    randn(100,2)*0.5-ones(100,2);
    randn(100,2)*0.75];

kmeansを使用して、学習データを 3 つのクラスターに分割します。

[idx,C] = kmeans(X,3);

クラスターとクラスター重心をプロットします。

figure
gscatter(X(:,1),X(:,2),idx,'bgm')
hold on
plot(C(:,1),C(:,2),'kx')
legend('Cluster 1','Cluster 2','Cluster 3','Cluster Centroid')

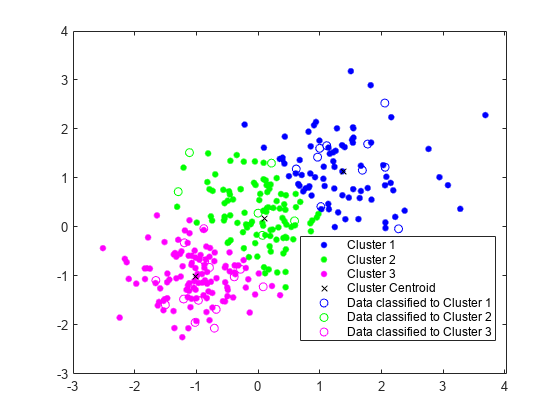
既存クラスターへの新しいデータの割り当て

検定データセットを生成します。

Xtest = [randn(10,2)*0.75+ones(10,2);
    randn(10,2)*0.5-ones(10,2);
    randn(10,2)*0.75];

既存のクラスターを使用して、検定データセットを分類します。pdist2を使用して、各検定データ点から最も近い重心を求めます。

[~,idx_test] = pdist2(C,Xtest,'euclidean','Smallest',1);

gscatter を使用して検定データをプロットします。idx_test を使用して検定データにラベルを付けます。

gscatter(Xtest(:,1),Xtest(:,2),idx_test,'bgm','ooo')
legend('Cluster 1','Cluster 2','Cluster 3','Cluster Centroid', ...
    'Data classified to Cluster 1','Data classified to Cluster 2', ...
    'Data classified to Cluster 3')

コードの生成

新しいデータを既存のクラスターに割り当てる C コードを生成します。C/C++ コードの生成には MATLAB® Coder™ が必要であることに注意してください。

重心位置と新しいデータを受け入れてから、pdist2を使用して最も近いクラスターを求める、findNearestCentroid という名前のエントリポイント関数を定義します。

MATLAB のアルゴリズムについてのコードを生成しようとしていることを指示するため、コンパイラ命令 %#codegen (またはプラグマ) をエントリポイント関数のシグネチャの後に追加します。この命令を追加すると、コード生成時にエラーになる違反の診断と修正を MATLAB Code Analyzer が支援します。

type findNearestCentroid % Display contents of findNearestCentroid.m

function idx = findNearestCentroid(C,X) %#codegen
[~,idx] = pdist2(C,X,'euclidean','Smallest',1); % Find the nearest centroid

メモ: このページの右上にあるボタンをクリックしてこの例を MATLAB® で開くと、MATLAB® で例のフォルダーが開きます。このフォルダーには、エントリポイント関数のファイルが含まれています。

codegen (MATLAB Coder)を使用してコードを生成します。C および C++ は静的な型の言語なので、エントリポイント関数内のすべての変数のプロパティをコンパイル時に決定しなければなりません。findNearestCentroid の入力のデータ型と配列サイズを指定するため、-args オプションを使用して、特定のデータ型および配列サイズをもつ一連の値を表す MATLAB 式を渡します。詳細については、コード生成用の可変サイズ引数の指定を参照してください。

codegen findNearestCentroid -args {C,Xtest}

codegen は、プラットフォームに依存する拡張子をもつ MEX 関数 findNearestCentroid_mex を生成します。

生成されたコードを検証します。

myIndx = findNearestCentroid(C,Xtest);
myIndex_mex = findNearestCentroid_mex(C,Xtest);
verifyMEX = isequal(idx_test,myIndx,myIndex_mex)

verifyMEX = logical
   1

isequal は、すべての入力が等しいことを意味する logical 1 (true) を返します。この比較により、同じインデックスを関数 pdist2、関数 findNearestCentroid、および MEX 関数が返すことを確認します。

GPU Coder™ を使用して、最適化された CUDA® コードを生成することもできます。

cfg = coder.gpuConfig('mex');
codegen -config cfg findNearestCentroid -args {C,Xtest}

コード生成の詳細については、一般的なコード生成のワークフローを参照してください。GPU Coder の詳細については、GPU Coder 入門 (GPU Coder)とサポートされる関数 (GPU Coder)を参照してください。

入力引数

X — データ

数値行列

データ。数値行列として指定します。X の行は観測値に対応し、列は変数に対応します。

X が数値ベクトルの場合、kmeans はこれを向きに関係なく n 行 1 列のデータ行列として扱います。

X の NaN は欠損データとして扱われ、最低 1 つの NaN を含む X の任意の行を削除します。X の行を削除することで標本サイズが減少します。関数 kmeans は、出力引数 idx の対応する値に対して NaN を返します。

データ型: single | double

k — クラスターの数

正の整数

データ内のクラスターの数。正の整数として指定します。

データ型: single | double

名前と値のペアの引数

オプションの Name,Value 引数のコンマ区切りペアを指定します。Name は引数名で、Value は対応する値です。Name は引用符で囲まなければなりません。Name1,Value1,...,NameN,ValueN のように、複数の名前と値のペアの引数を、任意の順番で指定できます。

例: 'Distance','cosine','Replicates',10,'Options',statset('UseParallel',1) は、コサイン距離、開始値の異なる 10 の複製クラスターおよび並列計算の使用を指定します。

'Display' — 表示する出力レベル

'off' (既定値) | 'final' | 'iter'

コマンド ウィンドウで表示する出力レベル。'Display' と次のいずれかのオプションから構成されるコンマ区切りのペアとして指定します。

• 'final' — 最後の反復の結果の表示

• 'iter' — 反復の結果の表示

• 'off' — 表示しない

例: 'Display','final'

'Distance' — 距離計量

'sqeuclidean' (既定値) | 'cityblock' | 'cosine' | 'correlation' | 'hamming'

最小化に使用する p 次元空間内の距離計量。'Distance' と 'sqeuclidean'、'cityblock'、'cosine'、'correlation' または 'hamming' から構成されるコンマ区切りのペアとして指定します。

kmeans は、サポートされている距離計量ごとに異なる方法で重心クラスターを計算します。次の表は、使用可能な距離計量をまとめたものです。式では、x は観測 (つまり X の行)、c は重心 (行ベクトル) です。

距離計量	説明	式
'sqeuclidean'	2 乗ユークリッド距離 (既定の設定)。各重心は、そのクラスターの点の平均です。	$$d(x,c)=(x-c)(x-c{)}^{\prime }$$
'cityblock'	L1 距離など、差の絶対値の総和。各重心は、そのクラスターの点の成分単位の中央値です。	$$d(x,c)={\displaystyle \sum _{j=1}^p\left|x_j-c_j\right|}$$
'cosine'	1 から、ベクトルとして扱われる点の間の夾角の余弦を引いた値。各重心は、そのクラスターの点を単位ユークリッド長に正規化した後の平均です。	$$d(x,c)=1-\frac{xc\prime }{\sqrt{\left(x{x}^{\prime }\right)\left(cc\prime \right)}}$$
'correlation'	1 から、値の系列として扱われる点の間の標本相関を引いた値。各重心は、そのクラスターの点を中心にシフトしてゼロ平均と単位標準偏差に正規化した後の、それらの点の成分単位の平均です。	ここで $$d(x,c)=1-\frac{\left(x-\overrightarrow{\overline{x}}\right){\left(c-\overrightarrow{\overline{c}}\right)}^{\prime }}{\sqrt{\left(x-\overrightarrow{\overline{x}}\right){\left(x-\overrightarrow{\overline{x}}\right)}^{\prime }}\sqrt{\left(c-\overrightarrow{\overline{c}}\right){\left(c-\overrightarrow{\overline{c}}\right)}^{\prime }}},$$ $$\overrightarrow{\overline{x}}=\frac{1}{p}\left({\displaystyle \sum _{j=1}^p{x}_j}\right){\overrightarrow{1}}_p$$ $$\overrightarrow{\overline{c}}=\frac{1}{p}\left({\displaystyle \sum _{j=1}^p{c}_j}\right){\overrightarrow{1}}_p$$ $${\overrightarrow{1}}_p$$ は p 個の 1 から構成される行ベクトルです。
'hamming'	この尺度はバイナリ データのみに適しています。 これは異なるビットの比率です。各重心は、そのクラスターの点の成分単位の中央値です。	$$d(x,y)=\frac{1}{p}{\displaystyle \sum }_{j=1}^{p}I\left\{x_j\ne y_j\right\},$$ I はインジケーター関数です。

例: 'Distance','cityblock'

'EmptyAction' — クラスターがそのメンバーである観測値をすべて失う場合に実行するアクション。

'singleton' (既定値) | 'error' | 'drop'

クラスターがそのメンバーである観測値をすべて失う場合に実行するアクション。'EmptyAction' と次のいずれかのオプションから構成されるコンマ区切りのペアとして指定します。

値	説明
'error'	空のクラスターを誤差として処理します。
'drop'	空になったすべてのクラスターを削除します。kmeans は、C および D 内の対応する戻り値を NaN に設定します。
'singleton'	その重心から最も遠くに位置する 1 つの点で構成される新しいクラスターを作成します (既定値)。

例: 'EmptyAction','error'

'MaxIter' — 最大反復回数

100 (既定値) | 正の整数

最大反復回数。'MaxIter' と正の整数で構成されるコンマ区切りのペアとして指定します。

例: 'MaxIter',1000

データ型: double | single

'OnlinePhase' — オンライン更新フラグ

'off' (既定値) | 'on'

オンライン更新フラグ。'OnlinePhase' および'off' または 'on' のいずれかで構成されるコンマ区切りのペアとして指定します。

OnlinePhase が on の場合、kmeans はバッチ更新フェーズだけでなくオンライン更新フェーズも実行します。オンライン フェーズは、大規模なデータセットでは時間がかかる場合がありますが、距離基準の局所的最小値になる解が保証されます。つまり、任意の 1 点を他のクラスターに移動すると距離の総和が増大するデータ分割を検出します。

例: 'OnlinePhase','on'

'Options' — 近似基準を最小化する反復アルゴリズムの制御オプション

[] (既定値) | statset によって返される構造体配列

近似基準を最小化する反復アルゴリズムの制御オプション。statset により返される 'Options' と構造体配列で構成されるコンマ区切りのペアとして指定します。構造体配列のサポートされているフィールドで、反復アルゴリズムを制御するオプションを指定します。

次の表は、サポートされているフィールドをまとめています。サポートされているフィールドでは Parallel Computing Toolbox™ が必要であることに注意してください。

フィールド	説明
'Streams'	RandStream オブジェクトまたはそのようなオブジェクトの cell 配列。Streams を指定しないと、kmeans には既定のストリームが使用されます。Streams を指定する場合、以下の条件がすべて満たされている場合を除き、単一オブジェクトを使用します。 開いている並列プールがある。 UseParallel が true。 UseSubstreams が false。 この場合は、並列プールと同じサイズの cell 配列を使用します。並列プールが開いていない場合、Streams は単一の乱数ストリームを提供しなければなりません。
'UseParallel'	true かつ Replicates > 1 である場合、kmeans は各複製に対して並列的に k-means アルゴリズムを実装します。 Parallel Computing Toolbox がインストールされていない場合、計算は逐次モードで行われます。既定の設定は false (逐次計算) です。
'UseSubstreams'	再生成可能な方法で並列計算する場合に true に設定します。既定の設定は false です。再現性のある計算を行うには、Streams をサブストリームを許可する型、'mlfg6331_64' または 'mrg32k3a' に設定します。

予測結果をより確実にするために、parpool (Parallel Computing Toolbox) を使用し、並列プールを明示的に作成してから kmeans を呼び出し 'Options',statset('UseParallel',1) を設定します。

例: 'Options',statset('UseParallel',1)

データ型: struct

'Replicates' — 新規の初期クラスター重心位置を使用するクラスタリングの反復回数

1 (既定値) | 正の整数

新規の初期クラスター重心位置を使用するクラスタリングの反復回数。'Replicates' と整数で構成されるコンマ区切りのペアとして指定します。kmeans は最低の sumd をもつ解を返します。

3-D 配列を名前と値のペアの引数 'Start' の値として指定することで、'Replicates' を暗黙的に設定できます。

例: 'Replicates',5

データ型: double | single

'Start' — 初期クラスター重心位置を選択する方法

'plus' (既定値) | 'cluster' | 'sample' | 'uniform' | 数値行列 | 数値配列

初期クラスター重心位置 (または "シード") を選択する方法。'Start' と 'cluster'、'plus'、'sample'、'uniform'、数値行列または数値配列から構成されるコンマ区切りのペアとして指定します。次の表は、シードの選択に使用可能なオプションをまとめています。

値	説明
'cluster'	X から 10% の副標本を無作為に抽出し、副標本内の観測値の個数が k より大きい場合は副標本に対して予備クラスタリング フェーズを実行します。この予備フェーズは 'sample' を使用して初期化されます。 無作為な 10% の副標本内の観測値の個数が k より小さい場合、k 個の観測値が X から無作為に選択されます。
'plus' (既定の設定)	クラスター中心の初期化に k-means++ アルゴリズムを実装して k シードを選択します。
'sample'	k 観測値を X から無作為に選択します。
'uniform'	k 点を一様に無作為に X の範囲から選択します。ハミング距離には無効です。
数値行列	k 行 p 列の行列の重心開始位置。Start の行はシードに対応します。Start の最初の次元から k が推測されるので、k に対して [] を渡すことができます。
数値配列	k x p x r の重心開始位置の配列。各ページの行はシードに対応します。3 番目の次元がクラスタリング ルーチンの複製を呼び出します。ページ j には複製 j のシードのセットが含まれています。3 番目次元の大きさから複製 (名前と値のペアの引数 'Replicates' により指定される) の数が推測されます。

例: 'Start','sample'

データ型: char | string | double | single

出力引数

idx — クラスター インデックス

数値列ベクトル

クラスター インデックス。数値列ベクトルとして返されます。idx には X と同数の行があり、各行は対応する観測のクラスター割り当てを示します。

C — クラスター重心位置

数値行列

クラスター重心位置。数値行列として返します。C は k 行 p 列の行列です。ここで、行 j はクラスター j の重心です。

sumd — 点と重心間の距離のクラスター内合計

数値列ベクトル

クラスター内での点から重心までの距離の合計。数値行ベクトルとして返されます。sumd は k 行 1 列のベクトルです。ここで要素 j はクラスター j 内の点と重心までの距離の合計です。既定の設定では、kmeans は二乗ユークリッド距離を使用します ('Distance' メトリクスを参照)。

D — 各点からすべての重心までの距離

数値行列

各点からそれぞれの重心までの距離。数値行列として返されます。D は n 行 k 列の行列です。ここで、要素 (j、m) は観測 j から重心 m までの距離です。既定の設定では、kmeans は二乗ユークリッド距離を使用します ('Distance' メトリクスを参照)。

詳細

k-means クラスタリング

"k-means クラスタリング" つまり、ロイドのアルゴリズム [2] は、データを分割する反復アルゴリズムであり、重心によって定義された k クラスターのうち 1 つに n 個の観測値をそれぞれ割り当てます。ここで、アルゴリズムを開始する前に k を選択します。

アルゴリズムは、以下のように実行されます。

1. k 初期クラスター中心 ("重心") を選択します。たとえば、観測 k を ('Start','sample' を使用して) 無作為に選択するか、クラスター中心の初期化 (既定の設定) にk-means++ アルゴリズムを使用します。

2. すべての観測について各重心までの、点とクラスター重心間の距離を計算します。

3. 以下の 2 つの進め方があります (OnlinePhase により指定)。

   • バッチの更新 ― 各観測を最も重心の近いクラスターに割り当てる。

   • オンライン更新 ― 再割り当てによりクラスター内合計、点とクラスター重心間の距離が減少する場合、観測を異なる重心に個別に割り当てる。

   詳細は、アルゴリズムを参照してください。

4. 各クラスター内の観測の平均を計算し、新規の重心位置 k を取得します。

5. クラスター割り当ての変化がなくなるか、反復回数が最大になるまで、手順 2 から 4 を繰り返します。

k-means++ アルゴリズム

"k-means++ アルゴリズム" は、経験則を使用して k-means クラスタリングの重心シードを検出します。Arthur および Vassilvitskii [1] によると、k-means++ はロイドのアルゴリズムの実行時間および最終的な解の質を改善します。

k-means++ アルゴリズムはクラスターの数を k と仮定して以下のようにシードを選択します。

1. 観測を一様に無作為にデータセット X から選択します。選択された観測値は最初の重心であり、c₁ で示されます。

2. 各観測から c₁ までの距離を計算します。c_j と観測値 m の間の距離を $$d\left(x_m,c_j\right)$$ と表します。

3. 次の重心 c₂ を次の確率で X から無作為に選択します。

   $$\frac{d^2\left(x_m,c_1\right)}{{\displaystyle \sum }_{j=1}^n{d}^2\left(x_j,c_1\right)}.$$

4. 中心 j を選択するには、以下を行います。

   1. 各観測から各重心までの距離を計算します。各観測を最も近い重心に割り当てます。

   2. m = 1、...、n および p = 1、...、j - 1 について、重心 j を次の確率で X から無作為に選択します。

      $$\frac{d^2\left(x_m,c_p\right)}{{\displaystyle \sum }_{\{h;x_h\in C_p\}}^{}{d}^2\left(x_h,c_p\right)},$$

      ここで、C_p は重心 c_p に最も近いすべての観測値の集合です。x_m は C_p に属します。

      つまり、それ自体から、既に選択されたなかで最も近い中心までの距離に比例する確率で、次の中心を選択します。

5. k 個の重心が選択されるまでステップ 4 を繰り返します。

Arthur と Vassilvitskii [1] は、複数のクラスター傾向のシミュレーション分析を使用して、k-means++ はロイドのアルゴリズムよりも、より低いクラスター内の点とクラスター重心間の距離の二乗和への収束を迅速に達成することを実証しました。

アルゴリズム

• kmeans は、2 つのフェーズの反復アルゴリズムを使用して、すべての k クラスターにわたって合計される点と重心間距離の総計を最小化します。

  1. 1 番目のフェーズでは、"バッチ更新" を使用します。つまり、各反復で、最も近いクラスターの重心に点を再割り当てするという操作をすべて同時に行ってから、クラスターの重心を再計算します。このフェーズでは、局所的最小値となる解に収束されないこともあります。つまり、1 つの点を他のクラスターに移動するデータ分割がと距離の総和を増大させます。これは、規模の小さなデータセットでよく発生します。バッチ フェーズは高速ですが、2 番目のフェーズの開始点となる解だけが概算される可能性があります。

  2. 2 番目のフェーズでは、"オンライン更新" を使用します。この更新では、点を個別に再割り当てし、再割り当てすることで距離の合計が減少する場合は、各再割り当ての後にクラスター重心を再計算します。このフェーズでの各反復は、すべての点を経過する 1 つの引き渡しで構成されます。このフェーズは局所的最小値に収束されます。ただし、距離の総和がより低い局所的最小値が他にある可能性もあります。一般に大域的最小値の検出は、開始点を網羅的に選択することで解決します。しかし、通常は無作為な開始点をもつ複製を複数使用すると、結果的に解は大域的最小値になります。

• Replicates = r > 1 および Start が plus (既定値) の場合、k-means++ アルゴリズムに従って、さまざまなシードの集合 r が選択される可能性もあります。

• Options の UseParallel オプションを有効にし、Replicates > 1 とした場合、各ワーカーはシードの選択とクラスター化を並列で行います。

参照

[1] Arthur, David, and Sergi Vassilvitskii. “K-means++: The Advantages of Careful Seeding.” SODA ‘07: Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms. 2007, pp. 1027–1035.

[2] Lloyd, Stuart P. “Least Squares Quantization in PCM.” IEEE Transactions on Information Theory. Vol. 28, 1982, pp. 129–137.

[3] Seber, G. A. F. Multivariate Observations. Hoboken, NJ: John Wiley & Sons, Inc., 1984.

[4] Spath, H. Cluster Dissection and Analysis: Theory, FORTRAN Programs, Examples. Translated by J. Goldschmidt. New York: Halsted Press, 1985.

拡張機能

tall 配列

メモリの許容量を超えるような多数の行を含む配列を計算します。

使用上の注意事項および制限事項:

• 以下の構文がサポートされます。

  • idx = kmeans(X,k)

  • [idx,C] = kmeans(X,k)

  • [idx,C,sumd] = kmeans(X,k)

  • [___] = kmeans(___,Name,Value)

• サポートされる名前と値のペアの引数および違いは次のとおりです。

  • 'Display' — 既定値は 'iter' です。

  • 'MaxIter'

  • 'Options' — statset によって作成される構造体配列の 'TolFun' フィールドのみをサポートします。'TolFun' の既定値は 1e-4 です。関数 kmeans は、点と重心の距離のクラスター内合計に対する終了許容誤差として 'TolFun' の値を使用します。たとえば、'Options',statset('TolFun',1e-8) を指定できます。

  • 'Replicates'

  • 'Start' — 'plus'、'sample' および数値配列のみをサポートします。

詳細は、メモリに収まらないデータの tall 配列を参照してください。

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意事項および制限事項:

• Start メソッドで無作為選択を使用する場合、クラスターの重心の初期位置が MATLAB^® と一致しない可能性があります。

• X の行数が固定されている場合、NaN が含まれている行はコード生成時に X から削除されません。

• C 内のクラスターの重心位置は、MATLAB の場合と順序が異なる可能性があります。この場合、idx 内のクラスターのインデックスも同様に異なります。

• Display を指定する場合、その値は 'off' でなければなりません。

• Streams を指定する場合、値が空でなければならず、UseSubstreams が false でなければなりません。

• UseParallel オプションを true に設定した場合、

  • Replicates が 1 である場合でも、一部の計算を並列実行できます。大規模なデータセットで Replicates が 1 の場合、UseParallel オプションを true に設定することを検討してください。

  • kmeans は parfor (MATLAB Coder) を使用して、サポートされる共有メモリ マルチコア プラットフォームで並列実行されるループを作成します。並列実行されるループは、単一のスレッドで実行されるループより高速になる可能性があります。コンパイラが Open Multiprocessing (OpenMP) アプリケーション インターフェイスをサポートしない場合、または OpenMP ライブラリを無効にした場合、MATLAB Coder™ は parfor ループを for ループとして扱います。サポートされるコンパイラについては、サポートされるコンパイラを参照してください。

• 生成されたコードを展開するデバイスのメモリを節約するため、kmeans と pdist2 をそれぞれ使用して、学習と予測を分離することができます。kmeans を使用して MATLAB でクラスターを作成し、生成されたコードで pdist2 を使用して新しいデータを既存のクラスターに割り当てます。コード生成用に、クラスターの重心位置と新しいデータセットを受け入れて最も近いクラスターのインデックスを返すエントリポイント関数を定義します。次に、エントリポイント関数のコードを生成します。たとえば、既存クラスターへの新しいデータの割り当てと C/C++ コードの生成を参照してください。

• R2020a 以降は、kmeans は、生成されたスタンドアロン C/C++ コードにおいて、倍精度のインデックスではなく、整数型 (int32) のインデックスを返します。そのため、関数は、単精度の入力を使用する場合、より厳密な単精度のサポートを可能にします。MEX コード生成では、関数は依然として MATLAB の動作に一致する倍精度のインデックスを返します。

コード生成の詳細については、コード生成の紹介および一般的なコード生成のワークフローを参照してください。

自動並列サポート

Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

並列実行するには、'UseParallel' オプションを true に設定します。

statset を使用してオプション構造体の 'UseParallel' フィールドを true に設定し、この関数を呼び出すときに名前と値のペアの引数 'Options' を指定します。

たとえば、次のようにします。'Options',statset('UseParallel',true)

詳細は、名前と値のペアの引数 'Options' を参照してください。

並列計算の全般的な情報については、自動並列サポートを使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

参考

clusterdata | gmdistribution | kmedoids | linkage | silhouette | statset | parpool (Parallel Computing Toolbox)

トピック

• k-means クラスタリングの解の比較
• k-means クラスタリングの紹介

R2006a より前に導入

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい