margin
Classification margins for naive Bayes classifier
Description
m = margin(Mdl,tbl,ResponseVarName)m) for the trained naive
Bayes classifier Mdl using the predictor data in table
tbl and the class labels in
tbl.ResponseVarName.
m = margin(Mdl,X,Y)Mdl using the predictor
data in matrix X and the class labels in
Y.
m is returned as a numeric vector with the same length as
Y. The software estimates each entry of
m using the trained naive Bayes classifier
Mdl, the corresponding row of X, and
the true class label Y.
Examples
Estimate Test Sample Classification Margins of Naive Bayes Classifier
Estimate the test sample classification margins of a naive Bayes classifier. An observation margin is the observed true class score minus the maximum false class score among all scores in the respective class.
Load the fisheriris data set. Create X as a numeric matrix that contains four petal measurements for 150 irises. Create Y as a cell array of character vectors that contains the corresponding iris species.
load fisheriris X = meas; Y = species; rng('default') % for reproducibility
Randomly partition observations into a training set and a test set with stratification, using the class information in Y. Specify a 30% holdout sample for testing.
cv = cvpartition(Y,'HoldOut',0.30);Extract the training and test indices.
trainInds = training(cv); testInds = test(cv);
Specify the training and test data sets.
XTrain = X(trainInds,:); YTrain = Y(trainInds); XTest = X(testInds,:); YTest = Y(testInds);
Train a naive Bayes classifier using the predictors XTrain and class labels YTrain. A recommended practice is to specify the class names. fitcnb assumes that each predictor is conditionally and normally distributed.
Mdl = fitcnb(XTrain,YTrain,'ClassNames',{'setosa','versicolor','virginica'})
Mdl =
ClassificationNaiveBayes
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'setosa' 'versicolor' 'virginica'}
ScoreTransform: 'none'
NumObservations: 105
DistributionNames: {'normal' 'normal' 'normal' 'normal'}
DistributionParameters: {3x4 cell}
Mdl is a trained ClassificationNaiveBayes classifier.
Estimate the test sample classification margins.
m = margin(Mdl,XTest,YTest); median(m)
ans = 1.0000
Display the histogram of the test sample classification margins.
histogram(m,length(unique(m)),'Normalization','probability') xlabel('Test Sample Margins') ylabel('Probability') title('Probability Distribution of the Test Sample Margins')

Classifiers that yield relatively large margins are preferred.
Select Naive Bayes Classifier Features by Examining Test Sample Margins
Perform feature selection by comparing test sample margins from multiple models. Based solely on this comparison, the classifier with the highest margins is the best model.
Load the fisheriris data set. Specify the predictors X and class labels Y.
load fisheriris X = meas; Y = species; rng('default') % for reproducibility
Randomly partition observations into a training set and a test set with stratification, using the class information in Y. Specify a 30% holdout sample for testing. Partition defines the data set partition.
cv = cvpartition(Y,'Holdout',0.30);Extract the training and test indices.
trainInds = training(cv); testInds = test(cv);
Specify the training and test data sets.
XTrain = X(trainInds,:); YTrain = Y(trainInds); XTest = X(testInds,:); YTest = Y(testInds);
Define these two data sets:
fullXcontains all predictors.partXcontains the last two predictors.
fullX = XTrain; partX = XTrain(:,3:4);
Train a naive Bayes classifier for each predictor set.
fullMdl = fitcnb(fullX,YTrain); partMdl = fitcnb(partX,YTrain);
fullMdl and partMdl are trained ClassificationNaiveBayes classifiers.
Estimate the test sample margins for each classifier.
fullM = margin(fullMdl,XTest,YTest); median(fullM)
ans = 1.0000
partM = margin(partMdl,XTest(:,3:4),YTest); median(partM)
ans = 1.0000
Display the distribution of the margins for each model using boxplots.
boxplot([fullM partM],'Labels',{'All Predictors','Two Predictors'}) ylim([0.98 1.01]) % Modify the y-axis limits to see the boxes title('Boxplots of Test Sample Margins')
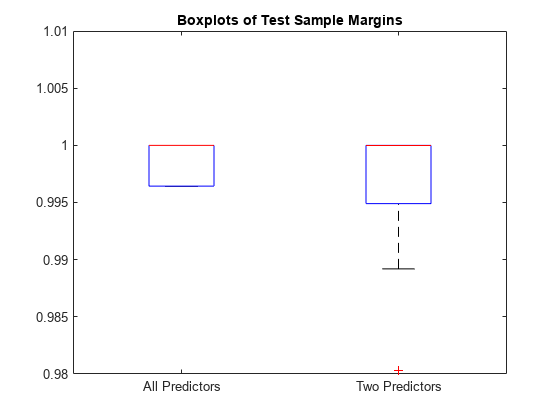
The margins for fullMdl (all predictors model) and partMdl (two predictors model) have a similar distribution with the same median. partMdl is less complex but has outliers.
Input Arguments
Mdl — Naive Bayes classification model
ClassificationNaiveBayes model object | CompactClassificationNaiveBayes model object
Naive Bayes classification model, specified as a ClassificationNaiveBayes model object or CompactClassificationNaiveBayes model object returned by fitcnb or compact,
respectively.
tbl — Sample data
table
Sample data used to train the model, specified as a table. Each row of
tbl corresponds to one observation, and each column corresponds
to one predictor variable. tbl must contain all the predictors used
to train Mdl. Multicolumn variables and cell arrays other than cell
arrays of character vectors are not allowed. Optionally, tbl can
contain additional columns for the response variable and observation weights.
If you train Mdl using sample data contained in a table, then the input
data for margin must also be in a table.
ResponseVarName — Response variable name
name of a variable in tbl
Response variable name, specified as the name of a variable
in tbl.
You must specify ResponseVarName as a character vector or string scalar.
For example, if the response variable y is stored as
tbl.y, then specify it as 'y'. Otherwise, the
software treats all columns of tbl, including y,
as predictors.
If tbl contains the response variable used to train
Mdl, then you do not need to specify
ResponseVarName.
The response variable must be a categorical, character, or string array, logical or numeric vector, or cell array of character vectors. If the response variable is a character array, then each element must correspond to one row of the array.
Data Types: char | string
X — Predictor data
numeric matrix
Predictor data, specified as a numeric matrix.
Each row of X corresponds to one observation (also known as an
instance or
example), and each column
corresponds to one variable (also known as a
feature). The variables in the
columns of X must be the same as the
variables that trained the Mdl
classifier.
The length of Y and the number of rows of X must
be equal.
Data Types: double | single
Y — Class labels
categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors
Class labels, specified as a categorical, character, or string array, logical or numeric
vector, or cell array of character vectors. Y must have the same data
type as Mdl.ClassNames. (The software treats string arrays as cell arrays of character
vectors.)
The length of Y must be equal to the number of rows of
tbl or X.
Data Types: categorical | char | string | logical | single | double | cell
More About
Classification Edge
The classification edge is the weighted mean of the classification margins.
If you supply weights, then the software normalizes them to sum to the prior probability of their respective class. The software uses the normalized weights to compute the weighted mean.
When choosing among multiple classifiers to perform a task such as feature section, choose the classifier that yields the highest edge.
Classification Margin
The classification margin for each observation is the difference between the score for the true class and the maximal score for the false classes. Margins provide a classification confidence measure; among multiple classifiers, those that yield larger margins (on the same scale) are better.
Posterior Probability
The posterior probability is the probability that an observation belongs in a particular class, given the data.
For naive Bayes, the posterior probability that a classification is k for a given observation (x1,...,xP) is
where:
is the conditional joint density of the predictors given they are in class k.
Mdl.DistributionNamesstores the distribution names of the predictors.π(Y = k) is the class prior probability distribution.
Mdl.Priorstores the prior distribution.is the joint density of the predictors. The classes are discrete, so
Prior Probability
The prior probability of a class is the assumed relative frequency with which observations from that class occur in a population.
Score
The naive Bayes score is the class posterior probability given the observation.
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
This function fully supports tall arrays. For more information, see Tall Arrays.
Version History
Introduced in R2014b
See Also
ClassificationNaiveBayes | CompactClassificationNaiveBayes | loss | predict | edge | fitcnb
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)