Vary Parameter Values and Obtain Multiple Transfer Functions
This example shows how to use the slLinearizer interface to batch linearize a Simulink® model. You vary model parameter values and obtain multiple open-loop and closed-loop transfer functions from the model.
You can perform the same analysis using the linearize function. However, when you want to obtain multiple open-loop and closed-loop transfer functions, especially for models that are expensive to compile repeatedly, slLinearizer can be more efficient.
Since the parameter variations in this example do not affect the operating point of the model, you batch linearize the model at a single operating point. If your application uses parameter variations that affect the model operating point, first trim the model for each parameter value combination. For an example that uses the linearize function, see Batch Linearize Model at Multiple Operating Points Derived from Parameter Variations.
Create slLinearizer Interface for Model
The scdcascade model used for this example contains a pair of cascaded feedback control loops. Each loop includes a PI controller. The plant models, G1 (outer loop) and G2 (inner loop), are LTI models.
Use the slLinearizer interface to analyze the inner-loop and outer-loop dynamics.
Open the model.
mdl = 'scdcascade';
open_system(mdl)

Use the slLinearizer function to create the interface.
sllin = slLinearizer(mdl)
slLinearizer linearization interface for "scdcascade":
No analysis points. Use the addPoint command to add new points.
No permanent openings. Use the addOpening command to add new permanent openings.
Properties with dot notation get/set access:
Parameters : []
OperatingPoints : [] (model initial condition will be used.)
BlockSubstitutions : []
Options : [1x1 linearize.LinearizeOptions]
The Command Window display shows information about the slLinearizer interface. In this interface, no parameters to vary are yet specified, so the Paramaeters property is empty.
Vary Inner-Loop Controller Gains
For inner-loop analysis, vary the gains of the inner-loop PI controller block, C2. Vary the proportional gain (Kp2) and integral gain (Ki2) in the 15% range.
Kp2_range = linspace(Kp2*0.85,Kp2*1.15,6); Ki2_range = linspace(Ki2*0.85,Ki2*1.15,4); [Kp2_grid, Ki2_grid] = ndgrid(Kp2_range,Ki2_range); params(1).Name = 'Kp2'; params(1).Value = Kp2_grid; params(2).Name = 'Ki2'; params(2).Value = Ki2_grid; sllin.Parameters = params;
Kp2_range and Ki2_range specify the sample values for Kp2 and Ki2. To obtain a transfer function for each combination of Kp2 and Ki2, use ndgrid and create a 6 x 4 parameter grid with grid arrays Kp2_grid and Ki2_grid. Configure the Parameters property of sllin with the structure params. This structure specifies the parameters to be varied and their grid arrays.
Analyze Closed-Loop Transfer Function for the Inner Loop
The overall closed-loop transfer function for the inner loop is equal to the transfer function from u1 to y2. To eliminate the effects of the outer loop, you can break the loop at e1, y1m, or y1. For this example, break the loop at e1.
Add u1 and y2 as analysis points, and e1 as a permanent opening of sllin.
addPoint(sllin,{'y2','u1'});
addOpening(sllin,'e1');
Obtain the transfer function from u1 to y2.
r2yi = getIOTransfer(sllin,'u1','y2');
r2yi, a 6 x 4 state-space model array, contains the transfer function for each specified parameter combination. The software uses the model initial conditions as the linearization operating point.
Because e1 is a permanent opening of sllin, r2yi does not include the effects of the outer loop.
Plot the step response for r2yi.
stepplot(r2yi);

The step response for all models varies in the 10% range and the settling time is less than 1.5 seconds.
Analyze Inner-Loop Transfer Function at the Plant Output
Obtain the inner-loop transfer function at y2, with the outer loop open at e1.
Li = getLoopTransfer(sllin,'y2',-1);
Because the software assumes positive feedback by default and scdcascade uses negative feedback, specify the feedback sign using the third input argument. Now, 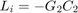 . The
. The getLoopTransfer command returns an array of state-space (ss) models, one for each entry in the parameter grid. The SamplingGrid property of Li matches the parameter values with the corresponding ss model.
Plot the bode response for  .
.
bodeplot(Li)

The magnitude plot for all the models varies in the 3-dB range. The phase plot shows the most variation, approximately 20°, in the [1 10] rad/s interval.
Vary Outer-Loop Controller Gains
For outer-loop analysis, vary the gains of the outer-loop PI controller block, C1. Vary the proportional gain (Kp1) and integral gain (Ki1) in the 20% range.
Kp1_range = linspace(Kp1*0.8,Kp1*1.2,6); Ki1_range = linspace(Ki1*0.8,Ki1*1.2,4); [Kp1_grid, Ki1_grid] = ndgrid(Kp1_range,Ki1_range); params(1).Name = 'Kp1'; params(1).Value = Kp1_grid; params(2).Name = 'Ki1'; params(2).Value = Ki1_grid; sllin.Parameters = params;
Similar to the workflow for configuring the parameter grid for inner-loop analysis, create the structure, params, that specifies a 6 x 4 parameter grid. Reconfigure sllin.Parameters to use the new parameter grid. sllin now uses the default values for Kp2 and Ki2.
Analyze Closed-Loop Transfer Function from Reference to Plant Output
Remove e1 from the list of permanent openings for sllin before proceeding with outer-loop analysis.
removeOpening(sllin,'e1');
To obtain the closed-loop transfer function from the reference signal, r, to the plant output, y1m, add r and y1m as analysis points to sllin.
addPoint(sllin,{'r','y1m'});
Obtain the transfer function from r to y1m.
r2yo = getIOTransfer(sllin,'r','y1m');
Plot the step response for r2yo.
stepplot(r2yo)

The step response is underdamped for all the models.
Analyze Outer-Loop Sensitivity at Plant Output
To obtain the outer-loop sensitivity at the plant output, add y1 as an analysis point to sllin.
addPoint(sllin,'y1');
Obtain the outer-loop sensitivity at y1.
So = getSensitivity(sllin,'y1');
Plot the step response of So.
stepplot(So)

The plot indicates that it takes approximately 15 seconds to reject a step disturbance at the plant output, y1.
Obtain Linearization Offsets
When batch linearizing for parameter variations, you can obtain the linearization offsets that correspond to the linearization operating points. To do so, set the StoreOffsets linearization option in the slLinearizer interface.
sllin.Options.StoreOffsets = true;
When you call a linearization function using sllin, you can return linearization offsets in the info structure.
[r2yi,info] = getIOTransfer(sllin,'u1','y2');
You can then use the offsets to configure an LPV System block. To do so, you must first convert the offsets to the required format. For an example that uses the linearize command, see LPV Approximation of Boost Converter Model.
offsets = getOffsetsForLPV(info);
Close the model.
bdclose(mdl)
See Also
slLinearizer | addPoint | addOpening | getIOTransfer | getLoopTransfer | getSensitivity | getCompSensitivity | linearize
Related Topics
- Batch Linearization Efficiency When You Vary Parameter Values
- Specify Parameter Samples for Batch Linearization
- Analyze Command-Line Batch Linearization Results Using Response Plots
- Vary Operating Points and Obtain Multiple Transfer Functions Using slLinearizer Interface
- Batch Linearize Model for Parameter Value Variations Using Model Linearizer
