このページは前リリースの情報です。該当の英語のページはこのリリースで削除されています。
代数方程式の線形システムを求解する
Algebraic Constraint ブロックを使用してシステムを解く

このモデルでは、次のようなベクトル化された形式で問題を表します。
![$$ \left[\begin{array}{cc} 1 & 1\\ -1& 1 \end{array}\right]\left[\begin{array}{c}z_1\\z_2\end{array}\right] =\left[\begin{array}{c}1\\1\end{array}\right] $$](../../examples/simulink/win64/SolveALinearSystemOfAlgebraicEquationsExample_eq00627851823494940069.png)

Algebraic Constraint ブロック 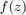 に送られる信号は、次の形式の
に送られる信号は、次の形式の 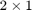 ベクトルです。
ベクトルです。
![$$\left[\begin{array}{c}z_1+z_2-1\\-z-1 + z_2-1\end{array}\right] $$](../../examples/simulink/win64/SolveALinearSystemOfAlgebraicEquationsExample_eq14029990663688292877.png)
ブロックは、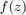 を 0 に制約するよう設定されています。したがって、
を 0 に制約するよう設定されています。したがって、 の解を求めると、解
の解を求めると、解 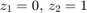 が出力されます。
が出力されます。
このページは前リリースの情報です。該当の英語のページはこのリリースで削除されています。
Algebraic Constraint ブロックを使用してシステムを解く

このモデルでは、次のようなベクトル化された形式で問題を表します。
![$$ \left[\begin{array}{cc} 1 & 1\\ -1& 1 \end{array}\right]\left[\begin{array}{c}z_1\\z_2\end{array}\right] =\left[\begin{array}{c}1\\1\end{array}\right] $$](../../examples/simulink/win64/SolveALinearSystemOfAlgebraicEquationsExample_eq00627851823494940069.png)

Algebraic Constraint ブロック 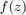 に送られる信号は、次の形式の
に送られる信号は、次の形式の 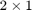 ベクトルです。
ベクトルです。
![$$\left[\begin{array}{c}z_1+z_2-1\\-z-1 + z_2-1\end{array}\right] $$](../../examples/simulink/win64/SolveALinearSystemOfAlgebraicEquationsExample_eq14029990663688292877.png)
ブロックは、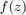 を 0 に制約するよう設定されています。したがって、
を 0 に制約するよう設定されています。したがって、 の解を求めると、解
の解を求めると、解 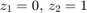 が出力されます。
が出力されます。