Finding a Signal in Data
This example shows how to use findsignal to find a time-varying signal in your data. It includes examples of how to find exact and closely matching signals by using a distance metric, how to compensate for a slowly varying offset, and the use of dynamic time-warping to allow for variations in sampling.
Finding Exact Matches
When you wish to find numerically exact matches of a signal, you can use strfind to perform the matching.
For example, if we have a vector of data:
data = [1 4 3 2 55 2 3 1 5 2 55 2 3 1 6 4 2 55 2 3 1 6 4 2];
and we want to find the location of the signal:
signal = [55 2 3 1];
we can use strfind to find the starting indices of where the signal exists in the data so long as the signal and data are numerically exact.
iStart = strfind(data,signal)
iStart = 1×3
5 11 18
Finding the Closest Matching Signal
strfind works well for numerically exact matches. However, this approach fails when there may be errors due to quantization noise or other artifacts in your signal.
For example, if you have a sinusoid:
data = sin(2*pi*(0:25)/16);
and you want to find the location of the signal:
signal = cos(2*pi*(0:10)/16);
strfind is unable to locate the sinusoid in the data which starts at the fifth sample:
iStart = strfind(data,signal)
iStart =
[]
strfind cannot find the signal in the data because, due to round-off error, not all values are numerically equal. To see this, subtract the data from the signal in the matching region.
data(5:15) - signal
ans = 1×11
10-15 ×
0 0 0 0.0555 0.0612 0.0555 0 0.2220 0 0.2220 0
There are numerical differences on the order of 1e-15.
To remedy this, you can use findsignal, which by default sweeps the signal across the data and computes the sum of the squared differences between the signal and data locally at each location, looking for the lowest sum.
To produce a plot of the signal and data where the best matching location is highlighted, you can call findsignal as follows:
findsignal(data,signal)

Finding the Closest Matches under a Threshold
By default findsignal always returns the closest match of the signal with the data. To return multiple matches, you can specify a bound on the maximum sum squared difference.
data = sin(2*pi*(0:100)/16);
signal = cos(2*pi*(0:10)/16);
findsignal(data,signal,'MaxDistance',1e-14)
findsignal returns matches in sorted order of closeness
[iStart, iStop, distance] = findsignal(data,signal,'MaxDistance',1e-14); fprintf('iStart iStop total squared distance\n')
iStart iStop total squared distance
fprintf('%4i %5i %.7g\n',[iStart; iStop; distance])5 15 0 37 47 0 69 79 0 21 31 1.776357e-15 53 63 1.776357e-15 85 95 1.776357e-15
Searching for a Complex Signal Trajectory with a Varying Offset
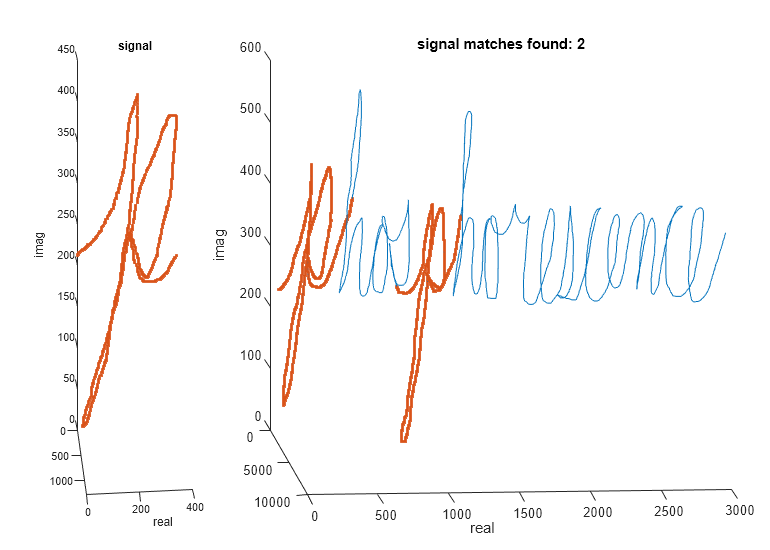
This next example shows how to use findsignal to find a signal that traces a known trajectory. The file "cursiveex.mat" contains a recording of the x- and y- position of the tip of a pen as it traced out the word "phosphorescence" on a piece of paper. The x,y data is encoded as the real and imaginary components of a complex signal, respectively.
load cursiveex plot(data) xlabel('real') ylabel('imag')

The same writer traced out a letter "p" as a template signal.
plot(signal) title('signal') xlabel('real') ylabel('imag')

You can find the first "p" in the data fairly easily using findsignal. This is because values of the signal line up fairly well at the beginning of the data.
findsignal(data,signal)

However, the second "p" has two characteristics that make it difficult for findsignal to identify: It has a significant but constant offset from the first letter, and parts of the letter were drawn at a different rate of speed than the template signal.
If you are interested in just matching the overall shape of the letter, you can subtract off a windowed local mean from both the signal and data element. This allows you to mitigate the effect of constant shifts.
To mitigate the effect of the varying speeds at which the letters are drawn, you can use dynamic time warping, which will stretch either the signal or data to a common time base as it performs the search:
findsignal(data,signal,'TimeAlignment','dtw', ... 'Normalization','center', ... 'NormalizationLength',600, ... 'MaxNumSegments',2)
Finding Time-Stretched Power Signals
This next example shows how to use findsignal to find the location of a spoken word in a phrase.
The following file contains an audio recording of the phrase: "Accelerating the pace of engineering and science" and a separate audio recording of "engineering" spoken by the same speaker.
load slogan
soundsc(phrase,fs)
soundsc(hotword,fs)It is common for the same speaker to vary the pronunciation of individual spoken words in a sentence or phrase. The speaker in this example pronounced "engineering" in two different ways: The speaker took roughly 0.5 seconds to pronounce the word in the phrase, stressing the second syllable ("en-GIN-eer-ing"); the same speaker took 0.75 seconds to pronounce the word in isolation, stressing the third syllable ("en-gin-EER-ing").
To compensate for these local variations in both time and volume, you can use a spectrogram to report the spectral power distribution as it evolves across time.
To get started, use a spectrogram with a fairly coarse frequency resolution. This is done to deliberately blur the narrow-band glottal pulses of the vocal tract, leaving just the wider-band resonances of the oral and nasal cavities undisturbed. This allows you to lock onto the spoken vowels of a word. Consonants (especially plosives and fricatives) are considerably more difficult to identify using spectrograms. The code below computes a spectrogram
Nwindow = 64; Nstride = 8; Beta = 64; Noverlap = Nwindow - Nstride; [~,~,~,PxxPhrase] = spectrogram(phrase, kaiser(Nwindow,Beta), Noverlap); [~,~,~,PxxHotWord] = spectrogram(hotword, kaiser(Nwindow,Beta), Noverlap);
Now that you have the spectrogram of the phrase and search word, you can use dynamic time warping to account for local variations in word length. Similarly, you can account for variations in power by using power normalization in conjunction with the symmetric Kullback-Leibler distance.
[istart,istop] = findsignal(PxxPhrase, PxxHotWord, ... 'Normalization','power','TimeAlignment','dtw','Metric','symmkl')
istart = 1144
istop = 1575
Plot and play the identified word.
findsignal(PxxPhrase, PxxHotWord, 'Normalization','power', ... 'TimeAlignment','dtw','Metric','symmkl')

soundsc(phrase(Nstride*istart-Nwindow/2 : Nstride*istop+Nwindow/2),fs)
