このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
回転機の振動解析
この例では、時間同期平均化および包絡線スペクトルを使用して、ギアボックスからの振動信号を解析する方法を示します。これらの機能は、特にギアボックスの予測メンテナンスに役立ちます。ギアボックスには、ギア、シャフト、ベアリングなどの複数の回転部品が含まれます。
この例では、シャフトが一定の速度で回転しているギアボックスの振動データを生成および解析します。時間同期平均化は、特定のシャフトまたはギアに関連付けられている振動成分を分離し、その他の成分を平均化するために使用されます。包絡線スペクトルは、高周波数の影響を引き起こす、局所化したベアリングの故障を識別するのに役立ちます。

35 歯ギアと 13 歯ピニオンの噛み合わせで構成される理想化されたギアボックスを考えてみます。ピニオンは、原動機に接続された入力シャフトに連結されています。ギアは、出力シャフトに接続されています。シャフトは、ギアボックスのハウジング上でローラー ベアリングに支えられています。2 つの加速度計 と がそれぞれ、ベアリングとギアボックスのハウジング上に配置されます。加速度計は、サンプル レート 20 kHz で動作します。
ピニオンは、 = 22.5 Hz または 1,350 rpm の速度で回転します。ギアおよび出力シャフトは、次のとおりです。
.
歯の噛み合い周波数 (ギアの噛み合い周波数とも呼ばれる) はギアおよびピニオンの歯が、次のように周期的にかみ合う速度です。
.
fs = 20E3; % Sample Rate (Hz) Np = 13; % Number of teeth on pinion Ng = 35; % Number of teeth on gear fPin = 22.5; % Pinion (Input) shaft frequency (Hz) fGear = fPin*Np/Ng; % Gear (Output) shaft frequency (Hz) fMesh = fPin*Np; % Gear Mesh frequency (Hz)
ピニオンおよびギアの振動波形を生成します。メイン シャフトのギア噛み合い周波数で発生する正弦波としての振動をモデル化します。20 秒の振動データを解析します。
ギア メッシュ波形には負荷を伝達する役割があり、それによって最も大きい振動振幅を持ちます。 は、2 つのシャフトおよびギア メッシュからの振動の寄与を記録します。この実験の場合、 によって記録される振動信号に対するベアリングの回転要素の寄与は、無視できると考えられます。ノイズのない振動信号の一部を可視化します。
t = 0:1/fs:20-1/fs; vfIn = 0.4*sin(2*pi*fPin*t); % Pinion waveform vfOut = 0.2*sin(2*pi*fGear*t); % Gear waveform vMesh = sin(2*pi*fMesh*t); % Gear-mesh waveform plot(t, vfIn + vfOut + vMesh) xlim([0 0.25]) xlabel('Time (s)') ylabel('Acceleration')
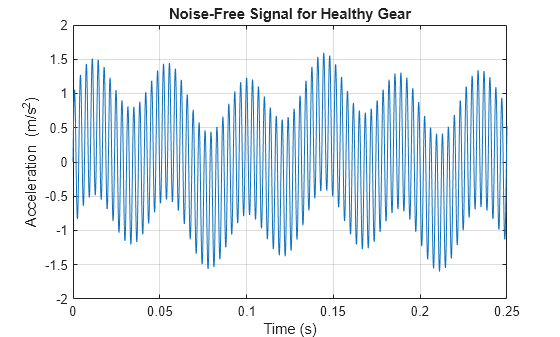
ギア歯の局所的な故障によって引き起こされる高周波数の影響の生成
ギア歯のいずれかが、破砕など、局所的な故障の影響を受けていると想定します。これは、ギアが回転するごとに 1 回発生する、高周波数の影響を引き起こします。

局所的な故障により、歯の噛み合わせの持続時間よりも短い持続時間をもつ影響が引き起こされます。ギア歯の表面のへこみにより、影響の持続時間中に、その高周波数の振動が生成されます。影響の周波数は、ギアボックスの部品のプロパティや固有振動数によって変わります。この例では、影響によって 1/fMesh (0.25 ミリ秒) の 8% の時間で 2 kHz の振動信号が発生すると任意で想定しています。ギアの回転ごとに、影響が 1 回繰り返されます。
ipf = fGear; fImpact = 2000; tImpact = 0:1/fs:2.5e-4-1/fs; xImpact = sin(2*pi*fImpact*tImpact)/3;
櫛形関数との畳み込みにより、影響を周期的にします。
xComb = zeros(size(t));
Ind = (0.25*fs/fMesh):(fs/ipf):length(t);
Ind = round(Ind);
xComb(Ind) = 1;
xPer = 2*conv(xComb,xImpact,'same');
シャフト信号に対して、故障信号 xPer を追加します。ホワイト ガウス ノイズを、故障がないギアと故障があるギアの両方の出力信号に追加し、 から出力をモデル化します。
vNoFault = vfIn + vfOut + vMesh; vFault = vNoFault + xPer; vNoFaultNoisy = vNoFault + randn(size(t))/5; vFaultNoisy = vFault + randn(size(t))/5;
時間履歴のセグメントを可視化します。影響の位置は、故障しているギアのプロット上に、逆向きの赤い三角形で示されます。それらは、ほとんど区別できません。
subplot(2,1,1) plot(t,vNoFaultNoisy) xlabel('Time (s)') ylabel('Acceleration') xlim([0.0 0.3]) ylim([-2.5 2.5]) title('Noisy Signal for Healthy Gear') subplot(2,1,2) plot(t,vFaultNoisy) xlabel('Time (s)') ylabel('Acceleration') xlim([0.0 0.3]) ylim([-2.5 2.5]) title('Noisy Signal for Faulty Gear') hold on MarkX = t(Ind(1:3)); MarkY = 2.5; plot(MarkX,MarkY,'rv','MarkerFaceColor','red') hold off
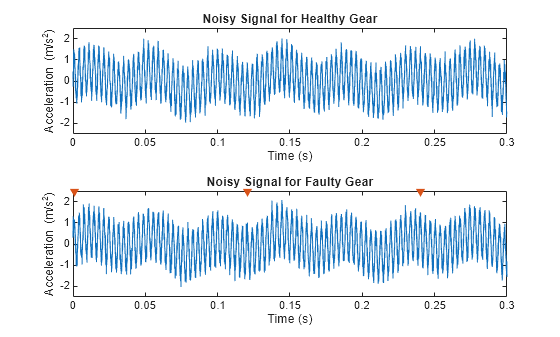
両方の信号のパワー スペクトルの比較
局所的な故障により、分散した側波帯がギア噛み合い周波数の近傍に、次のように出現します。
異常のないギアと故障したギアのスペクトルを計算します。シャフトの周波数 8.35 Hz と 22.5 Hz およびギア メッシュ周波数 292.5 Hz を含む周波数範囲を指定します。
[Spect,f] = pspectrum([vFaultNoisy' vNoFaultNoisy'],fs,'FrequencyResolution',0.2,'FrequencyLimits',[0 500]);
スペクトルをプロットします。故障はピニオンではなくギアに存在するため、側波帯は 、およびスペクトルで間隔があり離れている に出現することが予期されます。スペクトルは、fGear, fPin および fMesh で予期されたピークを示します。ただし、信号にノイズが存在する場合は、 での側波帯のピークが区別できなくなります。
figure plot(f,10*log10(Spect(:,1)),f,10*log10(Spect(:,2)),':') xlabel('Frequency (Hz)') ylabel('Power Spectrum (dB)') hold on plot(fGear,0,'rv','MarkerFaceColor','red') plot(fPin,0,'gv','MarkerFaceColor','green') plot(fMesh,0,'bv','MarkerFaceColor','blue') hold off legend('Faulty','Healthy','f_{Gear}','f_{Pinion}','f_{Mesh}')
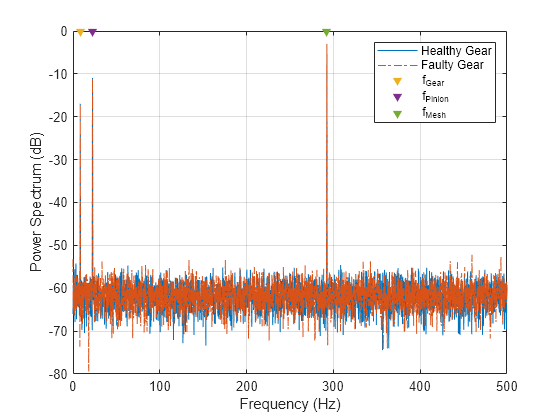
ギア メッシュ周波数の近傍にズームインします。 と で、ギアおよびピニオンの側波帯のグリッドを作成します。
figure p1 = plot(f,10*log10(Spect(:,1))); xlabel('Frequency (Hz)') ylabel('Power Spectrum (dB)') xlim([250 340]) ylim([-70 -40]) hold on p2 = plot(f,10*log10(Spect(:,2))); harmonics = -5:5; SBandsGear = (fMesh+fGear.*harmonics); [X1,Y1] = meshgrid(SBandsGear,ylim); SBandsPinion = (fMesh+fPin.*harmonics); [X2,Y2] = meshgrid(SBandsPinion,ylim); p3 = plot(X1,Y1,':r'); p4 = plot(X2,Y2,':k'); hold off legend([p1 p2 p3(1) p4(1)],{'Faulty Gear';'Healthy Gear';'f_{sideband,Gear}';'f_{sideband,Pinion}'})

ピークがギアの側波帯 と整列するかどうかは明確ではありません。
出力振動信号に対する時間同期平均化の適用
ギアの側波帯 、およびピニオンの側波帯 のピークを分離することは困難です。前の節では、ピークの分離、および故障による影響を受けているのがピニオンかギアかを判定することの難しさを示しました。時間同期平均化は、ゼロ平均ランダム ノイズと特定のシャフトの周波数と関連付けられていない波形の平均を出します。これにより、故障検出の処理が容易になります。
関数 tsa を使用して、ピニオンとギア両方の時間同期した波形を生成します。
ピニオンの時間同期したパルスを指定します。ピニオンの 10 回転に対する時間同期平均を計算します。
tPulseIn = 0:1/fPin:max(t);
taPin = tsa(vFaultNoisy,fs,tPulseIn,'NumRotations',10);ギアの時間同期したパルスを指定します。ギアの 10 回転に対する時間同期平均を計算します。
tPulseOut = 0:1/fGear:max(t);
taGear = tsa(vFaultNoisy,fs,tPulseOut,'NumRotations',10);1 回の回転に対する時間同期した信号を可視化します。影響は、ギアに対する時間同期平均化信号では比較的容易に確認できますが、ピニオン シャフトでは平均化されます。プロット上にマーカー付きで示される影響の位置は、隣接するギア メッシュのピークよりも振幅が大きくなります。
出力引数なしの関数 The tsa は、現在の Figure において各信号セグメントに対応する時間同期平均信号および時間領域信号をプロットします。
figure subplot(2,1,1) tsa(vFaultNoisy,fs,tPulseIn,'NumRotations',10) xlim([0.5 1.5]) ylim([-2 2]) title('TSA Signal for Pinion') subplot(2,1,2) tsa(vFaultNoisy,fs,tPulseOut,'NumRotations',10) xlim([0.5 1.5]) ylim([-2 2]) title('TSA Signal for Gear') hold on plot(1.006,2,'rv','MarkerFaceColor','red') hold off
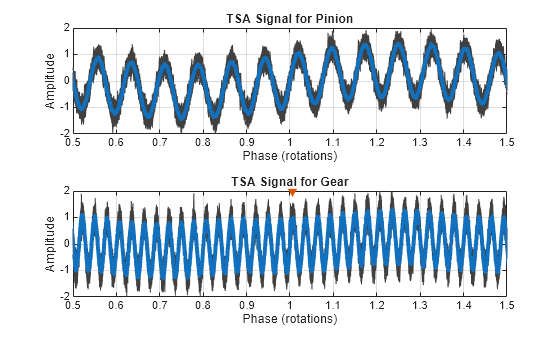
時間同期平均信号のパワー スペクトルの可視化
時間同期平均したギアの信号のパワー スペクトルを計算します。ギア メッシュ周波数 292.5 Hz のそれぞれの側で、15 のギア側波帯を含む周波数範囲を指定します。 にピークが現れています。
figure pspectrum(taGear,fs,'FrequencyResolution',2.2,'FrequencyLimits',[200 400]) harmonics = -15:15; SBandsGear=(fMesh+fGear.*harmonics); [X1,Y1] = meshgrid(SBandsGear,ylim); [XM,YM] = meshgrid(fMesh,ylim); hold on plot(XM,YM,'--k',X1,Y1,':r') legend('Power Spectra','Gear-Mesh Frequency','f_{sideband,Gear}') hold off title('TSA Gear (Output Shaft)')

同じ周波数範囲で時間同期平均したピニオンの信号のパワー スペクトルを可視化します。ここでは、 の周波数の位置にグリッド ラインをプロットします。
figure pspectrum(taPin,fs,'FrequencyResolution',5.8,'FrequencyLimits',[200 400]) SBandsPinion = (fMesh+fPin.*harmonics); [X2,Y2] = meshgrid(SBandsPinion,ylim); [XM,YM] = meshgrid(fMesh,ylim); hold on plot(XM,YM,'--b',X2,Y2,':k') legend('Power Spectra','Gear-Mesh Frequency','f_{sideband,Pinion}') hold off title('TSA Pinion (Input Shaft)')

プロットで、 には目立ったピークがありません。
元の信号のパワー スペクトルには、ノイズに加え、2 つの異なるシャフトの波形が含まれています。側波帯の高調波を区別することは困難です。しかし、時間同期平均したギアの信号のスペクトルにおいて、側波帯の位置で目立つピークを観察します。また、側波帯の振幅の不均性も観察します。これは、ギアで局所的な故障のインジケーターです。一方で、時間同期平均したピニオンの信号では、側波帯のピークはありません。これにより、ピニオンには異常がない可能性があるという結論を出すことができます。
関連しない波形を平均化することにより、関数 tsa では、側波帯の高調波を確認して故障のあるギアを識別できます。この機能は、複数のシャフトやギアを備えたギアボックスから単一のシャフトに対応する振動信号を抽出することが望ましい場合に、特に役立ちます。
分散した故障のピニオンへの追加とその影響の振動信号への組み込み
離心率やギアの不整列 [1] などの分散したギアの故障は、ギア メッシュ周波数の整数倍のまわりで狭くグループ化された高レベルの側波帯を引き起こします。

分散した故障をシミュレートするには、ギア メッシュ周波数のそれぞれの側で振幅が減少する 3 つの側波帯成分を取り込みます。
SideBands = -3:3; SideBandAmp = [0.02 0.1 0.4 0 0.4 0.1 0.02]; % Sideband amplitudes SideBandFreq = fMesh + SideBands*fPin; % Sideband frequencies vSideBands = SideBandAmp*sin(2*pi*SideBandFreq'.*t);
振動信号に対して、側波帯信号を追加します。この結果として、振幅変調が発生します。
vPinFaultNoisy = vFaultNoisy + vSideBands;
分散した故障によって影響されるギアボックスの時間履歴の一部を可視化します。
plot(t,vPinFaultNoisy) xlim([0.6 0.85]) xlabel('Time (s)') ylabel('Acceleration') title('Effects of Sideband Modulation')
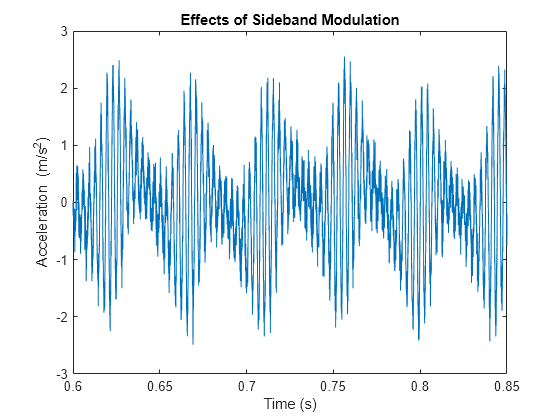
ピニオンおよびギアの時間同期平均信号を再計算します。
taPin = tsa(vPinFaultNoisy,fs,tPulseIn,'NumRotations',10); taGear = tsa(vFaultNoisy,fs,tPulseOut,'NumRotations',10);
時間同期平均信号のパワー スペクトルを可視化します。ピニオンの時間同期平均信号の 3 つの側波帯は、より顕著になります。これは、分散した故障が存在することを示します。しかし、時間同期平均したギアの信号のスペクトルは変化がないままです。
subplot(2,1,1) pspectrum(taPin,fs,'FrequencyResolution',5.8,'FrequencyLimits',[200 400]) hold on plot(X2,Y2,':k') legend('Power Spectrum','f_{sideband,Pinion}','Location','south') hold off title ('TSA Pinion (Input Shaft)') subplot(2,1,2) pspectrum(taGear,fs,'FrequencyResolution',2.2,'FrequencyLimits',[200 400]) hold on plot(X1,Y1,':r') legend('Power Spectrum','f_{sideband,Gear}') hold off title ('TSA Gear (Output Shaft)')
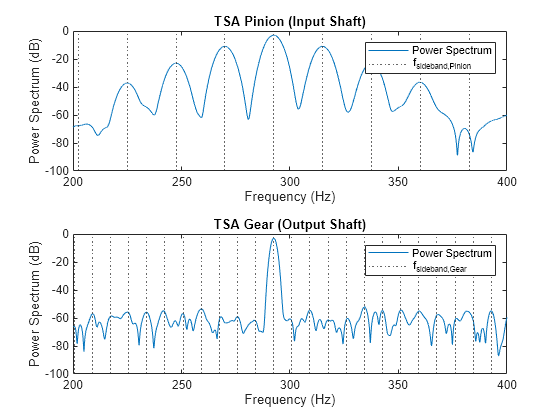
結論として、関数 tsa は、ギアおよびピニオンの寄与を振動信号全体から抽出することに役立ちます。これはさらに、局所化し、分散した故障に影響される特定の部品を識別するのに役立ちます。
回転要素のベアリングの故障の振動解析
回転要素のベアリングの局所化した故障は、外輪、内輪、ケージ、または回転要素で発生する可能性があります。これらの故障はぞれぞれ、固有の周波数による特徴をもちます。これは通常、製造元によってリストが作成されているか、またはベアリングの仕様から計算されます。局所化した故障の影響により、ギアボックス構造内のベアリングと応答変換器の間で高周波数振動が生成されます [2]。ギアボックス内のギアには異常がなく、ピニオン シャフトを支えるベアリングの 1 つが内輪の局所化した故障によって影響を受けると想定します。解析では、ラジアル荷重の影響は無視します。

ピッチの直径 12 cm のベアリングは、8 つの回転要素をもっています。各回転要素の直径は 2 cm です。接触角 は です。ベアリングの振動の解析時には、加速度計をベアリング ハウジングに配置するのが一般的な方法です。加速度の測定は、故障のあるベアリング ハウジングに配置された加速度計 によって記録されます。
ベアリングのパラメーターを定義します。
n = 8; % Number of rolling element bearings d = 0.02; % Diameter of rolling elements p = 0.12; % Pitch diameter of bearing thetaDeg = 15; % Contact angle in degrees
影響は、回転要素が内輪上の局所的な故障を通過するたびに発生します。これが発生する率は、内輪転動体通過周波数 (BPFI) です。BPFI は、次を使用して計算できます。
.
bpfi = n*fPin/2*(1 + d/p*cosd(thetaDeg))
bpfi = 104.4889
カイザー ウィンドウによってウィンドウを適用した 3 kHz の正弦波として、各影響をモデル化します。欠陥があると、ベアリングで 5 ミリ秒の一連の影響を引き起こします。初期段階の穴や破砕でのインパルスは約 100 kHz までの広い周波数範囲に対応します [2]。
fImpact = 3000; tImpact = 0:1/fs:5e-3-1/fs; xImpact = sin(2*pi*fImpact*tImpact).*kaiser(length(tImpact),40)';
櫛形関数との畳み込みにより、影響を周期的にします。 はベアリングに近いため、 によって記録されるギアボックスの振動信号で顕著になるように、影響の振幅を調整します。
xComb = zeros(size(t));
xComb(1:round(fs/bpfi):end) = 1;
xBper = 0.33*conv(xComb,xImpact,'same');打撃信号を可視化します。
figure plot(t,xBper) xlim([0 0.05]) xlabel('Time (s)') ylabel('Acceleration') title('Impacts Due to Local Fault on the Inner Race of the Bearing')

異常がないギアボックスからの振動信号に対して、周期的なベアリングの故障を追加します。
vNoBFaultNoisy = vNoFault + randn(size(t))/5; vBFaultNoisy = xBper + vNoFault + randn(size(t))/5;
信号のスペクトルを計算します。より低い周波数で、スペクトルを可視化します。最初の 10 の BPFI 高調波のグリッドを作成します。
pspectrum([vBFaultNoisy' vNoBFaultNoisy' ],fs,'FrequencyResolution',1,'FrequencyLimits',[0 10*bpfi]) legend('Damaged','Healthy') title('Bearing Vibration Spectra') grid off harmImpact = (0:10)*bpfi; [X,Y] = meshgrid(harmImpact,ylim); hold on plot(X/1000,Y,':k') legend('Healthy','Damaged','BPFI harmonics') xlim([0 10*bpfi]/1000) hold off
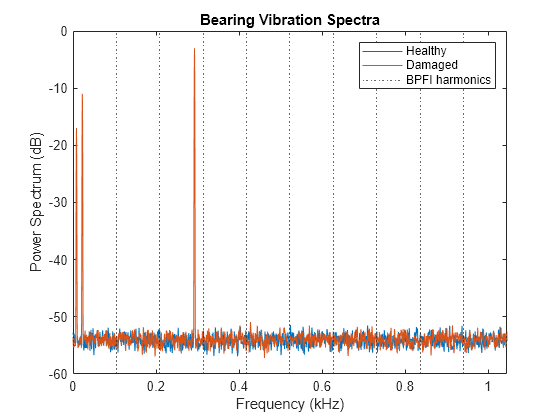
スペクトルの下端では、シャフトおよびメッシュの周波数や、それらの次数により、その他の特徴が不明確になります。異常がないベアリングのスペクトルと破損したベアリングのスペクトルは、区別できません。この欠陥は、ベアリングの故障を分離できるアプローチの必要性を強調するものです。
BPFI は、 と接触角のコサイン の比率に依存します。BPFI に対する無理式は、ベアリングの影響がシャフトの回転の整数値と同期していないことを示します。関数 tsa は影響を平均化してしまうため、この場合には便利ではありません。影響は、平均化される各セグメントにおいて同じ位置に存在するわけではありません。
関数 envspectrum (包絡線スペクトル) は、振幅復調を実行します。また、高周波数の影響に関する情報を抽出するのに役立ちます。
包絡線信号とそれらのスペクトルを計算してプロットします。ベアリングの故障がある信号とない信号に対して包絡線スペクトルを比較します。より低い周波数で、スペクトルを可視化します。最初の 10 の BPFI 高調波のグリッドを作成します。
figure envspectrum([vNoBFaultNoisy' vBFaultNoisy'],fs) xlim([0 10*bpfi]/1000) [X,Y] = meshgrid(harmImpact,ylim); hold on plot(X/1000,Y,':k') legend('Healthy','Damaged','BPFI harmonics') xlim([0 10*bpfi]/1000) hold off
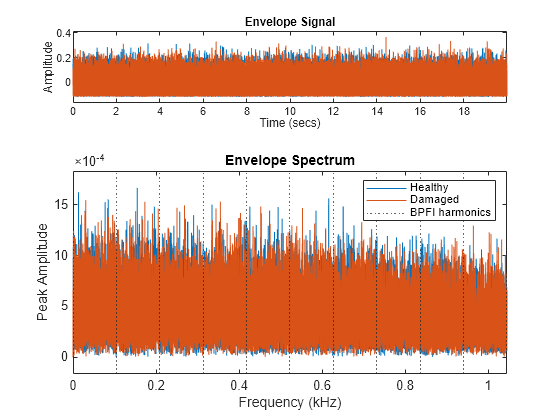
信号がノイズによって汚染されているため、BPFI ピークが包絡線スペクトルで突出していないことを観察します。ノイズを平均化するために tsa を実行すると、影響の信号も平均化してしまうため、ベアリングの故障の解析では有効でないことを思い出してください。
関数 envspectrum は、対象となる帯域外のノイズを除去するために使用できる、組み込みフィルターを提供します。次数 200 で、中心が 3.125 kHz および幅 4.167 kHz のバンドパス フィルターを適用します。
Fc = 3125; BW = 4167; envspectrum([vNoBFaultNoisy' vBFaultNoisy'],fs,'Method','hilbert','FilterOrder',200,'Band',[Fc-BW/2 Fc+BW/2]) harmImpact = (0:10)*bpfi; [X,Y] = meshgrid(harmImpact,ylim); hold on plot(X/1000,Y,':k') legend('Healthy','Damaged','BPFI harmonics') xlim([0 10*bpfi]/1000) hold off

包絡線スペクトルは、通過帯域の内容を、ベースバンドに有効に取り込みます。そのため、1 kHz 未満の BPFI 高調波の突出したピークの存在を示します。これにより、ベアリングの内輪は損傷している可能性があるという結論を出すことができます。
この場合、故障したベアリングの周波数スペクトルは、影響を及ぼす周波数によって変調された BPFI 高調波を明確に示します。この現象を、影響の周波数 3 kHz に近いスペクトル内で可視化します。
figure pspectrum([vBFaultNoisy' vNoBFaultNoisy'],fs,'FrequencyResolution',1,'FrequencyLimits',(bpfi*[-10 10]+fImpact)) legend('Damaged','Healthy') title('Bearing Vibration Spectra')

ピーク間の周波数の間隔が BPFI と等しいことを観察します。
まとめ
この例では、ピニオンとギアの両方に関連付けられる振動信号を分離するため、時間同期平均を使用しています。さらに、tsa はランダム ノイズを減衰させました。速度 (および負荷 [2]) が変動する場合、次数トラッキングを tsa の事前処理として使用して、シャフトの回転角度について信号をリサンプルすることができます。また、実験的状況下では、時間同期平均を使用し、シャフト速度における小さい変化の影響を減衰します。
ベアリングの故障解析では [3]、適切な開始地点としてブロードバンド周波数解析を使用できる場合があります。ただし、その有用性は、ギアボックス内のギア メッシュ周波数の高調波が高い場合など、ベアリングの影響周波数の近傍のスペクトルが他の成分の寄与を含む場合に限定されます。そのような状況では、包絡線解析が有用です。関数 envspectrum を使用し、ベアリングの摩耗や損傷のインジケーターとして、故障のあるベアリングに対して包絡線信号およびスペクトルを抽出できます。
参考文献
Scheffer, Cornelius, and Paresh Girdhar.Practical Machinery Vibration Analysis and Predictive Maintenance.Amsterdam: Elsevier, 2004.
Randall, Robert Bond.Vibration Based Condition Monitoring: Industrial, Aerospace and Automotive Applications.Chichester, UK: John Wiley and Sons, 2011.
Lacey, S. J. An Overview of Bearing Vibration Analysis.(http://www.maintenanceonline.co.uk/maintenanceonline/content_images/p32-42%20Lacey%20paper%20M&AM.pdf より)
Brandt, Anders. Noise and Vibration Analysis: Signal Analysis and Experimental Procedures. Chichester, UK: John Wiley and Sons, 2011.
参考
envspectrum | pspectrum | tsa
