不等間隔サンプル信号のスペクトル解析

不等間隔サンプル信号

不等間隔サンプル信号は、自動車業界、通信および医学や天文学などの多様な分野でよく見られます。不等間隔サンプリングの原因としては、センサーの不完全さ、クロックの不一致またはイベントでトリガーされる現象などが考えられます。

スペクトル成分の計算と研究は信号解析では重要です。ピリオドグラムやウェルチ法などの従来のスペクトル解析テクニックでは、入力信号が等間隔サンプルでなければなりません。サンプリングが不等間隔である場合は、信号を等間隔サンプル グリッドにリサンプリングまたは内挿できます。しかしこれにより、望ましくないアーティファクトがスペクトルに追加されることがあり、解析エラーにつながる場合があります。

より良い方法は、Lomb-Scargle 法を使用することです。これは不等間隔サンプルを直接処理するため、リサンプリングや内挿が不要になります。アルゴリズムは関数 plomb に実装されています。

データの欠損がある信号のスペクトル解析

マイクロコントローラーが室温を記録して、測定値を 15 分ごとにクラウドベースのサーバーに送信し、データがそこに保存される温度監視システムを検討します。インターネットへの接続が不調なため、クラウドベースのシステムが、マイクロコントローラーから送信された測定値の一部を受信できないことが分かっています。また、測定期間中に少なくとも 1 回マイクロコントローラーのバッテリーが切れたため、サンプリングに大きなギャップがあります。

温度測定値と対応するタイムスタンプを読み込みます。

load('nonuniformdata.mat','roomtemp','t1')

figure
plot(t1/(60*60*24*7),roomtemp,'LineWidth',1.2)

grid
xlabel('Time (weeks)')
ylabel('Temperature (\circF)')

信号が等間隔サンプルかどうかを判断する簡単な方法は、連続するサンプリング時間の間隔のヒストグラムをとることです。

サンプリング間隔 (時間の差) のヒストグラムを分単位でプロットします。サンプルが存在するポイントのみを含めます。

tAtPoints = t1(~isnan(roomtemp))/60;
TimeIntervalDiff = diff(tAtPoints);

figure
hist(TimeIntervalDiff,0:100)
grid
xlabel('Sampling intervals (minutes)')
ylabel('Occurrences')
xlim([10 100])

測定値の大部分は、想定されるように約 15 分間隔になっています。しかし、サンプリング間隔が 30 分および 45 分前後のものもかなりあり、1 つまたは 2 つの連続するサンプルの欠損を示しています。このため、この信号は不等間隔サンプルになります。さらに、ヒストグラムではバーの周囲のジッターが多いことがわかります。これは TCP/IP のレイテンシに関係している可能性があります。

Lomb-Scargle 法を使用して、信号のスペクトル成分を計算して可視化します。スペクトルをより見やすくするため、0.02 mHz までの周波数を考慮します。これは、週あたり約 13 サイクルに相当します。

[Plomb,flomb] = plomb(roomtemp,t1,2e-5,'power');

figure
plot(flomb*60*60*24*7,Plomb)
grid
xlabel('Frequency (cycles/week)')
ylabel('Power (dBW)')

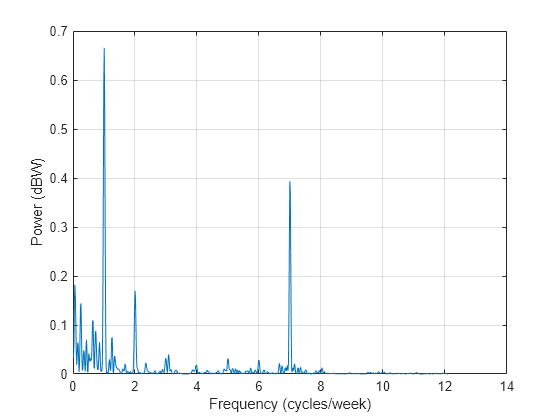
スペクトルから、週 7 サイクルと週 1 サイクルの周期性が優勢であることがわかります。これは、このデータが 7 日周期のカレンダーに従って温度管理が行われる建物からのものであることを考えると理解できます。週 1 サイクルのピークを示すスペクトル線は、建物内の温度が週末には温度が低く、平日には温度が高いという週次サイクルに従うことを示します。週 7 サイクルのスペクトル線は、夜間に温度が低く、日中高くなる一日単位のサイクルもあることを示しています。

サンプルが等間隔ではない信号のスペクトル解析

心拍変動 (HRV) 信号は、心拍の経時的な生理的変動を示すものですが、人間の心拍は一定ではないため、通常サンプリングは等間隔ではありません。HRV 信号は心電図 (ECG) の読み取り値から得られます。

HRV 信号のサンプル ポイントは ECG の R ピーク時にあります。各ポイントの振幅は、連続する R ピーク間の時間差の逆数として計算され、次の R ピークの瞬間に得られます。

% Load the signal, the timestamps, and the sample rate
load('nonuniformdata.mat','ecgsig','t2','Fs')

% Find the ECG peaks
[pks,locs] = findpeaks(ecgsig,Fs, ...
    'MinPeakProminence',0.3,'MinPeakHeight',0.2);

% Determine the RR intervals
RLocsInterval = diff(locs);

% Derive the HRV signal
tHRV = locs(2:end);
HRV = 1./RLocsInterval;

% Plot the signals
figure
a1 = subplot(2,1,1); 
plot(t2,ecgsig,'b',locs,pks,'*r')
grid
a2 = subplot(2,1,2);
plot(tHRV,HRV)
grid
xlabel(a2,'Time(s)')
ylabel(a1,'ECG (mV)')
ylabel(a2,'HRV (Hz)')

R ピーク間の間隔の変動により、HRV データのサンプル時間の不均一が生じます。信号のピーク位置を考慮し、間隔のヒストグラムを秒単位でプロットします。

figure
hist(RLocsInterval)

grid
xlabel('Sampling interval (s)')
ylabel('RR distribution')

通常、HRV スペクトルの対象の周波数帯域は以下のとおりです。

これらの帯域は、HRV に寄与する目立った生理的調整メカニズムの周波数範囲をほぼカバーしています。これらの帯域の変動があれば、生理的に意味があります。

plomb を使用して、HRV 信号のスペクトルを計算します。

figure
plomb(HRV,tHRV,'Pd',[0.95, 0.5])

破線は 95% および 50% の検出確率を示します。これらのしきい値は、ピークの統計的有意性を測定します。スペクトルには、上記の 3 つの対象帯域すべてでピークが示されています。ただし、VLF 範囲の 23.2 mHz にあるピークのみが検出確率 95% を示しています。その他のピークは検出確率が 50% 未満です。40 mHz より下にあるピークは、温度調節系要因やホルモン要因といった長期的な調整メカニズムによるものと考えられます。