シミュレートされたシステムおよび風力タービンブレードのモード解析

この例では次を使用します。

この例では、周波数応答関数 (FRF) およびモーダルパラメーターを実験データから推定する方法を示します。最初のセクションでは、シミュレーション実験で 3 自由度 (3DOF) システムを一連のハンマー打撃で励起し、結果の変位を記録します。構造の 3 つのモードについて、周波数応答関数、固有振動数、減衰比およびモード形状ベクトルを推定します。2 番目のセクションでは、風力タービンブレードの実験から推定された周波数応答関数からモード形状ベクトルを推定します。タービンブレードの測定設定および結果のモード形状を可視化します。この例には、System Identification Toolbox (TM) が必要です。

シミュレーションされるビームの固有振動数および減衰

単入力/単出力のハンマー励起

一連のハンマー打撃により 3DOF システムを励起し、センサーで結果の変位を記録します。システムは比例的に減衰され、減衰行列が質量および剛性行列の線形結合となります。

励起信号、応答信号、時間信号およびグラウンドトゥルース周波数応答関数を含む 2 セットの測定のデータをインポートします。応答信号の最初のセット Y1 は最初の質量の変位を測定し、2 番目の Y2 は 2 番目の質量を測定します。各励起信号は 10 個の連結されたハンマー打撃から構成され、各応答信号には対応する変位が含まれます。各打撃信号の持続時間は 2.53 秒です。励起および応答信号には加法性ノイズが存在します。最初の測定における最初の励起および応答チャネルを可視化します。

[t,fs,X1,X2,Y1,Y2,f0,H0] = helperImportModalData();
X0 = X1(:,1);
Y0 = Y1(:,1);
helperPlotModalAnalysisExample([t' X0 Y0]);

最初の励起および応答チャネルの FRF を動的柔軟性に関して計算してプロットしますが、これは力に対する変位の測定です [1]。既定の設定では、FRF はウィンドウが適用されたセグメントのスペクトルを平均して計算します。各ハンマー励起が実質的に減衰してから次の励起が開始するため、箱型ウィンドウを使用できます。センサーを変位として指定します。

winLen = 2.5275*fs; % window length in samples
modalfrf(X0,Y0,fs,winLen,'Sensor','dis')

既定の 'H1' 推定器を使用して推定された FRF には、測定された周波数帯域に 3 つの顕著なピークが含まれ、振動の 3 つの柔軟なモードに対応します。コヒーレンスはこれらのピーク付近では 1 に近く、応答測定の S/N 比が低い反共振領域では低くなります。1 に近いコヒーレンスは推定の質が高いことを示します。'H1' の推定は、ノイズが出力測定にのみ存在する場合に最適ですが、'H2' 推定器は、入力にのみ加法性ノイズが存在する場合に最適です [2]。この FRF の 'H1' および 'H2' 推定値を計算します。

[FRF1,f1] = modalfrf(X0,Y0,fs,winLen,'Sensor','dis');  % Calculate FRF (H1)
[FRF2,f2] = modalfrf(X0,Y0,fs,winLen,'Sensor','dis','Estimator','H2');

著しい測定ノイズがある場合、または励起が不十分な場合、パラメトリック法を使用すると、データから FRF を正確に抽出する追加オプションが得られます。「部分空間」法は最初にデータ [3] に対して状態空間モデルを適用してから、周波数応答関数を計算します。状態空間モデルの次数 (極の数に等しい) および直達の有無を指定して、状態空間推定を設定できます。

[FRF3,f3] = modalfrf(X0,Y0,fs,winLen,'Sensor','dis','Estimator','subspace','Feedthrough',true);

ここで、直達項および 1:10 の範囲で最適な次数を含む状態空間モデルを適用することで、FRF3 が推定されます。'H1'、'H2'、および 'subspace' の手法を使用して、推定された FRF と理論的な FRF を比較します。

helperPlotModalAnalysisExample(f1,FRF1,f2,FRF2,f3,FRF3,f0,H0);

推定器は応答ピーク付近では同等に機能しますが、'H2' 推定器は反共振では応答を過大に推定します。コヒーレンスは推定器の選択の影響を受けません。

次に、ピーク選択アルゴリズムを使用して各モードの固有振動数を推定します。ピーク選択アルゴリズムは、シンプルで高速な手続きで FRF のピークを識別します。これはローカルメソッドであるため、各推定が単一の周波数応答関数から生成されます。また、単一自由度 (SDOF) 法でもあるため、各モードのピークが個別に考慮されます。その結果、モーダルパラメーターのセットが各 FRF に対して生成されます。前のプロットに基づいて、3 つのピークが含まれる 200 ～ 1600 Hz の周波数範囲を指定します。

fn = modalfit(FRF1,f1,fs,3,'FitMethod','PP','FreqRange',[200 1600])

固有振動数はおよそ 373、853 および 1371 Hz です。再構成された FRF をプロットし、modalfit を使用して測定したデータと比較します。FRF は、周波数応答関数の行列 FRF1 から推定されたモーダルパラメーターを使用して再構成されます。modalfit を出力引数を指定せずに再度呼び出し、再構成された FRF を含むプロットを生成します。

modalfit(FRF1,f1,fs,3,'FitMethod','PP','FreqRange',[200 1600])

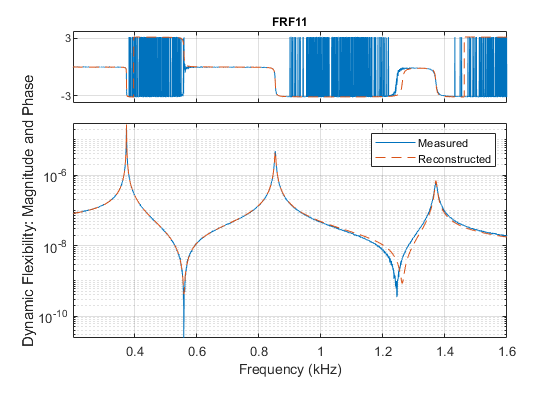
再構成された FRF は、最初の励起および応答チャネルの測定された FRF と一致します。次の節では、2 つの追加の励起位置を検討します。

ロービングハンマー励起

既定の 'H1' 推定器を使用し、3 つすべてのセンサーの応答について FRF を計算してプロットします。ロービングハンマー励起であるため、測定タイプを 'rovinginput' として指定します。

modalfrf(X1,Y1,fs,winLen,'Sensor','dis','Measurement','rovinginput')

前のセクションでは、単一の FRF から単一セットのモーダルパラメーターを計算しました。今度は、最小二乗複素指数 (LSCE) アルゴリズムを使用してモーダルパラメーターを推定します。LSCE および LSRF アルゴリズムは、複数の応答信号を同時に解析して、単一セットのモーダルパラメーターを生成します。これらはグローバルな多自由度 (MDOF) 法であるため、複数の周波数応答関数からすべてのモードのパラメーターが同時に推定されます。

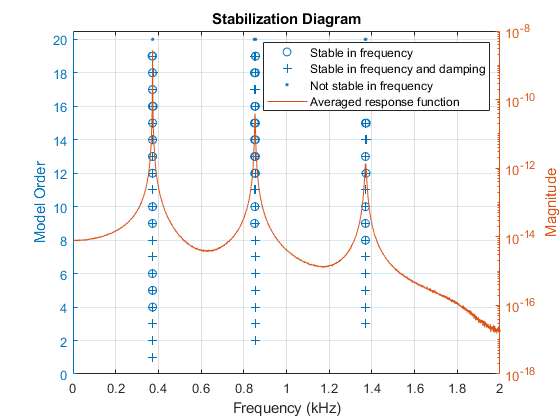
LSCE アルゴリズムは計算モードを生成しますが、これは物理的に構造には存在しません。安定化ダイアグラムを使用し、モード数の増加に伴う極の安定性を調べて物理モードを特定します。物理モードの固有振動数および減衰比は、同じ位置にとどまる (すなわち安定している) 傾向があります。安定化ダイアグラムを作成し、周波数が安定している極の固有振動数を出力します。

[FRF,f] = modalfrf(X1,Y1,fs,winLen,'Sensor','dis','Measurement','rovinginput');
fn = modalsd(FRF,f,fs,'MaxModes',20, 'FitMethod', 'lsce'); % Identify physical modes

既定では、極の固有振動数の変化が 1% 未満の場合、極は周波数が安定しているとして分類されます。周波数が安定している極は、減衰比の変化が 5% 未満の場合、さらに減衰が安定しているとして分類されます。両方の基準を異なる値に調整できます。安定した極の位置に基づいて、固有振動数として 373、852.5 および 1371 Hz を選択します。これらの周波数は、他の周波数が安定した極の固有振動数と共に、modalsd の出力 fn に含まれます。物理的に存在するモード数より高いモデル次数は、一般に、LSCE アルゴリズムを使用して良好なモーダルパラメーターの推定を生成するために必要です。この場合、4 つのモードのモデル次数で 3 つの安定した極を示します。目的の振動数は fn の 4 行目の最初の 3 列に出現します。

physFreq = fn(4,[1 2 3]);

固有振動数と減衰を推定し、再構成および測定された FRF をプロットします。安定性ダイアグラム 'PhysFreq' から決定される 4 つのモードおよび物理周波数を指定します。modalfit は、指定したモードのモーダルパラメーターのみを返します。

modalfit(FRF,f,fs,4,'PhysFreq',physFreq)

[fn1,dr1] = modalfit(FRF,f,fs,4,'PhysFreq',physFreq)

次に、FRF を計算し、センサー位置が異なる 2 番目のセットのハンマー打撃の安定化ダイアグラムをプロットします。安定化基準を周波数の場合は 0.1%、減衰の場合は 2.5% に変更します。

[FRF,f] = modalfrf(X2,Y2,fs,winLen,'Sensor','dis','Measurement','rovinginput');
fn = modalsd(FRF,f,fs,'MaxModes',20,'SCriteria',[0.001 0.025]);

より厳密な基準にすると、大部分の極が周波数が不安定として分類されます。周波数および減衰が安定している極は平均された FRF とかなりの程度で一致しており、これらが測定データに存在することが示唆されます。

physFreq = fn(4,[1 2 3]);

この測定のセットにおけるモーダルパラメーターを抽出し、測定の最初のセットにおけるモーダルパラメーターと比較します。励起および応答測定が一致する位置に対応する駆動点 FRF のインデックスを指定します。固有振動数の差は 1% 以内、減衰比の差は 4% 未満のため、モーダルパラメーターは測定と測定の間で一致することが示されます。

[fn2,dr2] = modalfit(FRF,f,fs,4,'PhysFreq',physFreq,'DriveIndex',[1 2])

Tdiff2 = table((fn1-fn2)./fn1,(dr1-dr2)./dr1,'VariableNames',{'diffFrequency','diffDamping'})

Tdiff2 =

  3x2 table

    diffFrequency    diffDamping
    _____________    ___________

      2.9972e-06      -0.031648 
     -5.9335e-06     -0.0099076 
       1.965e-05      0.0001186

モーダルパラメーター推定に対してパラメトリック法を使用すると、FRF に測定ノイズがある場合や FRF が高いモーダル密度を示している場合にピーク選択および LSCE の手法として役立つ代替方法が得られます。最小二乗有理関数 (LSRF) アプローチは、分母を共有する伝達関数を多入力、多出力 FRF に適用し、それによって単一のモーダルパラメーターのグローバルな推定 [4] を取得します。LSRF のアプローチを使用した手順は、LSCE と類似しています。安定化ダイアグラムを使用して静止モードを識別し、識別した物理周波数に対応するモーダルパラメーターを抽出できます。

[FRF,f] = modalfrf(X1,Y1,fs,winLen,'Sensor','dis','Measurement','rovinginput');
fn = modalsd(FRF,f,fs,'MaxModes',20, 'FitMethod', 'lsrf'); % Identify physical modes using lsfr
physFreq = fn(4,[1 2 3]);
[fn3,dr3] = modalfit(FRF,f,fs,4,'PhysFreq',physFreq,'DriveIndex',[1 2],'FitMethod','lsrf')

Tdiff3 = table((fn1-fn3)./fn1,(dr1-dr3)./dr1,'VariableNames',{'diffFrequency','diffDamping'})

Tdiff3 =

  3x2 table

    diffFrequency    diffDamping
    _____________    ___________

     -7.8599e-06      0.007982  
         0.56255       0.83086  
         0.37799       0.37626

パラメトリック法についての最後のノートは、次のとおりです。FRF 推定法 ('subspace') およびモーダルパラメーター推定法 ('lsrf') は、動的モデルを時間領域信号や周波数応答関数に対して適用するために System Identification Toolbox で使用するものと類似しています。このツールボックスを使用できる場合、tfest や ssest などのコマンドを使用して、データを適用するためのモデルを識別できます。compare および resid コマンドを使用して、識別されたモデルの品質を評価できます。モデルの品質を検証すると、それらをモデルパラメーターの抽出に使用できます。これは、状態空間推定器を使用して、簡潔に示されます。

Ts = 1/fs; % sample time
% Create a data object to be used for model estimation.
EstimationData = iddata(Y0(1:1000), X0(1:1000), 1/fs);
% Create a data object to be used for model validation
ValidationData = iddata(Y0(1001:2000), X0(1001:2000), 1/fs);

直達項を含む 6 次の連続時間状態空間モデルを識別します。

sys = ssest(EstimationData, 6, 'Feedthrough', true)

sys =
  Continuous-time identified state-space model:
      dx/dt = A x(t) + B u(t) + K e(t)
       y(t) = C x(t) + D u(t) + e(t)
 
  A = 
            x1       x2       x3       x4       x5       x6
   x1    4.041    -1765    149.8    -1880   -49.64     -358
   x2     1764  -0.3434     2197   -232.5   -438.3   -128.4
   x3   -152.4    -2198    2.839     4715    255.9    547.5
   x4     1880    228.2    -4714   -15.91    -1216   -28.79
   x5    59.42    440.9   -275.5     1217    35.03    -8508
   x6    363.7    120.2   -545.4   -44.02     8508   -92.47
 
  B = 
            u1
   x1   0.2777
   x2  -0.6085
   x3  0.07123
   x4   -3.658
   x5  0.04771
   x6   -7.642
 
  C = 
               x1          x2          x3          x4          x5          x6
   y1    4.46e-05  -5.315e-06   -7.46e-06  -1.641e-05   2.964e-06  -5.871e-06
 
  D = 
              u1
   y1  7.997e-09
 
  K = 
               y1
   x1   3.513e+07
   x2  -3.244e+06
   x3  -3.598e+07
   x4  -1.059e+07
   x5   1.724e+08
   x6   7.521e+06
 
Parameterization:
   FREE form (all coefficients in A, B, C free).
   Feedthrough: yes
   Disturbance component: estimate
   Number of free coefficients: 55
   Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.

Status:                                                    
Estimated using SSEST on time domain data "EstimationData".
Fit to estimation data: 99.26% (prediction focus)          
FPE: 1.355e-16, MSE: 1.304e-16

検証データに対してどれほど適切に適用されるかをチェックすることで、モデルの品質を評価します。

clf
compare(ValidationData, sys)  % plot shows good fit

モデル sys を使用してモーダルパラメーターを計算します。

[fn4, dr4] = modalfit(sys, f, 3);

風力タービンブレードのモード形状ベクトル

風力タービンブレードの動的挙動を理解することは、運転効率を最適化し、ブレードの故障を予測するために重要です。このセクションでは、風力タービンブレードの実験的なモード解析データを解析し、ブレードのモード形状を可視化します。ハンマーでタービンブレードの 20 個の位置を励起し、基準加速度計で位置 18 の応答を測定します。アルミニウムブロックはブレードの土台に取り付けられ、ブレードはブレードのフラップ部分に対して垂直なフラップ方向に励起されます。各位置の FRF を収集します。FRF データはマサチューセッツ大学ローウェル校の Structural Dynamics and Acoustics Systems Laboratory により提供されました。まず、測定位置の空間的配置を可視化します。

位置 18 および 20 の風力タービンブレードの FRF 推定を読み込んでプロットします。最初のいくつかのピークを拡大します。

[FRF,f,fs] = helperImportModalData();
helperPlotModalAnalysisExample(FRF,f,[18 20]);

最初の 2 つのモードは 37 Hz および 111 Hz 付近のピークとして現れます。安定化ダイアグラムをプロットして、固有振動数を推定します。モデル次数 14 について返される最初の 2 つの値は、周波数および減衰比が安定しています。

fn = modalsd(FRF,f,fs,'MaxModes',20);
physFreq = fn(14,[1 2]);

次に、modalfit を使用して、最初の 2 つのモードのモード形状を抽出します。前のプロットに基づいて、近似を周波数範囲 0 ～ 250 Hz に制限します。

[~,~,ms] = modalfit(FRF,f,fs,14,'PhysFreq',physFreq,'FreqRange',[0 250]);

モード形状は、各位置における構造の各モードの運動振幅を定量化します。モード形状ベクトルを推定するには、周波数応答関数の行列の 1 つの行または列が必要です。実際には、これは構造 (この場合はロービングハンマー) のすべての測定位置に励起が必要なこと、またはすべての位置の応答測定が必要なことを意味します。モード形状を可視化するには、FRF の虚数部を調べます。ブレードの片側にある位置の FRF 行列における虚数部のウォーターフォールダイアグラムをプロットします。周波数範囲を最大 150 Hz に制限して、最初の 2 つのモードを調べます。プロットのピークがモード形状を表します。

measlocs = [3 6 9 11 13 15 17 19 20]; % Measurement locations on blade edge
helperPlotModalAnalysisExample(FRF,f,measlocs,150);

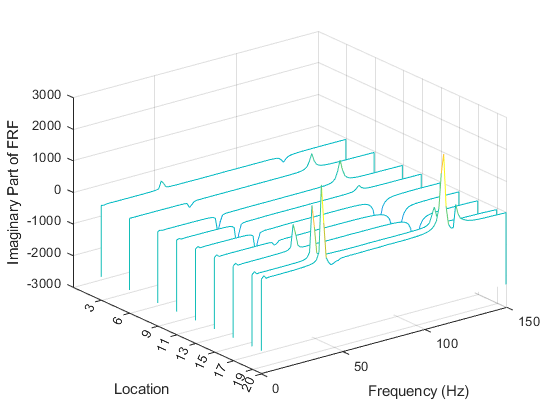
ピークの等高線によりプロットに示された形状は、ブレードの最初と 2 番目の曲げモーメントを表します。次に、同じ測定位置について、モード形状ベクトルの大きさをプロットします。

helperPlotModalAnalysisExample(ms,measlocs);

振幅はスケーリングが異なりますが (モード形状ベクトルはモーダル 1 の A に対してスケーリングされる)、モード形状の等高線は形状が一致します。最初のモードの形状には大きな先端の変位および 2 つのノードがあり、振動振幅はゼロです。2 番目のモードにも大きな先端の変位および 3 つのノードがあります。

まとめ

この例では、ロービングハンマーによって励起される 3DOF システムに関してシミュレートされたモード解析データセットを解析して比較しました。LSCE と LSRF アルゴリズムおよび安定化ダイアグラムを使用して、固有振動数および減衰を推定しました。モーダルパラメーターは 2 セットの測定において一致しました。個別のケースで、FRF 行列の虚数部およびモード形状ベクトルを使用して、風力タービンブレードのモード形状を可視化しました。

謝辞

風力タービンブレードの実験データをご提供いただいたマサチューセッツ大学ローウェル校 Structural Dynamics and Acoustics Systems Laboratory の Peter Avitabile 博士に謝意を申し上げます。

参考文献

[1] Brandt, Anders.Noise and Vibration Analysis: Signal Analysis and Experimental Procedures. Chichester, UK: John Wiley and Sons, 2011.

[2] Vold, Håvard, John Crowley, and G. Thomas Rocklin."New Ways of Estimating Frequency Response Functions."Sound and Vibration.Vol. 18, November 1984, pp. 34-38.

[3] Peter Van Overschee and Bart De Moor."N4SID: Subspace Algorithms for the Identification of Combined Deterministic-Stochastic Systems." Automatica.Vol. 30, January 1994, pp. 75-93.

[4] Ozdemir, A. A., and S. Gumussoy."Transfer Function Estimation in System Identification Toolbox via Vector Fitting."Proceedings of the 20th World Congress of the International Federation of Automatic Control.Toulouse, France, July 2017.

参考

modalfit | modalfrf | modalsd

シミュレートされたシステムおよび風力タービン ブレードのモード解析

シミュレーションされるビームの固有振動数および減衰

風力タービン ブレードのモード形状ベクトル

まとめ

謝辞

参考文献

参考

シミュレートされたシステムおよび風力タービンブレードのモード解析

風力タービンブレードのモード形状ベクトル