このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
産業用 3 自由度ロボット: ベクトル/行列パラメーターを使用した MIMO システムの C MEX ファイル モデリング
この例では、スカラー、ベクトル、行列パラメーターを使用する C MEX モデル ファイルの設計方法を説明します。モデル化の基礎として、多少理想化された産業用ロボットを使用します。ここでは、導出された状態空間方程式の左辺は明示的に与えられていません。わかりやすくするため、複数の実験データを同定部分で使用します。
Manutec R3 ロボットのモデル化
検討するロボットの Manutec r3 は、Siemens の子会社である Manutec が製造したものです。実際には、ロボットには 6 種類のリンクがあり、3 つはツールを中央に位置決めし、3 つはツール自体の方向を決めます。ここで、ツールの中央への移動に関して 3 自由度をもつロボットのモデル化のみを検討します。ロボットのコンポーネントは、自由度 1 の回転ジョイントで接続された剛体としてモデル化されます。ギア ボックスでの摩擦およびその他の複雑な現象、およびモーターとセンサーのダイナミクスは無視されます。このように簡略化しても、結果として得られるモデル構造は複雑になります。
以下で実施される同定実験に使用されるモデル構造は、次の文献で詳細に記述されています。
M. Otter、S. Turk 著『The DFVLR Models 1 and 2 of the Manutec r3 Robot』Institute for Robotics and System Dynamics、German Aerospace Research Establishment (DLR)、Oberpfaffenhofen、1988 年 5 月
また、簡略化された Manutec r3 ロボットに基づくパラメーター推定は、次の書籍でこれまでに検討されています。
K. Schittkowski 著『Numerical Data Fitting in Dynamical Systems』Kluwer Academic Publishers、239-242 ページ、2002 年
図 1 に、Manutec r3 ロボットの概略図を示します。

図 1: Manutec r3 ロボットの概略図
簡略化した Manutec r3 ロボットのダイナミクスは、ベクトル方程式で与えられます。
d^2 d
M(q(t)) ---- q(t) = F(u(t)) + G(q(t)) + H(-- q(t), q(t))
dt^2 dt
ここで、列ベクトル q(t) = [q_1(t), q_2(t), q_3(t)]' は、アーム 0 が土台の座標に対応する状態で、i = 1、2、3 のときのアーム i-1 とアーム i の間の相対角度を示します。3 つのモーターに適用されるトルク制御 u(t) = [u_1(t) u_2(t) u_3(t)]^T は、ロボットを動かす外力を表します。これらの信号が個々にスケーリングされて (力係数 Fc(1)、Fc(2) および Fc(3) を使用)、駆動力を提供します。
F(u(t)) = [Fc(1)*u_1(t) Fc(2)*u_2(t) Fc(3)*u_3(t)]'
質量行列 M(q(t)) は複雑な 3 行 3 列の対称正定値行列で、次の要素があります。
M(1, 1) = c_1(p) + c_2(p)*cos(q_2(t))^2 + c_3(p)*sin(q_2(t))^2 +
c_4(p)*cos(q_2(t)+q_3(t)) + c_5(p)*sin(q_2(t)+q_3(t)) +
c_6(p)*sin(q_2(t))*sin(q_2(t)+q_3(t))
M(1, 2) = c_7(p)*cos(q_2(t)) + c_8(p)*cos(q_2(t)+q_3(t))
M(1, 3) = c_9(p)*cos(q_2(t)+q_3(t))
M(2, 1) = M(1, 2)
M(2, 2) = c_10(p) + c_11(p)*cos(q_3(t))
M(2, 3) = c_12(p) + c_13(p)*cos(q_3(t))
M(3, 1) = M(1, 3)
M(3, 2) = M(2, 3)
M(3, 3) = c_14(p)
ここで、c_1(p)、...、c_14(p) はロボット パラメーター p の 14 の関数です。
ロボットは 2 つのその他の力の影響も受けます。最初の力は G(q(t)) で、重力によって発生し、次の要素をもちます。
G_1(p) = 0
G(p) = G_2(p) = b_1(p)*sin(q_2(t)) + b_2(p)*sin(q_2(t)+q_3(t))
G_3(p) = b_3(p)*sin(q_2(t)+q_3(t))
ここで、b_1(p)、...、b_3(p) はパラメーター p の 3 つの関数です。2 番目の力 h(d/dt q(t), q(t)) はコリオリ力および遠心力によって生じ、Christoffel 記号によって計算されます。
d d d
g_ijk = -0.5*(-------- M(i, j) + -------- M(i, k) - -------- M(j, k))
d q_k(t) d q_j(t) d q_k(t)
は、次のように計算されます。
d 3 3 d d
H_i(-- q(t), q(t)) = sum(sum(g_ijk*-- q_k(t))*-- q_j(t))
dt j=1 k=1 dt dt
for i = 1, 2, 3.
質量行列 M(q(t)) は可逆 (物理的に対象となる角度について) で、ロボットのダイナミクスは次のように記述できます。
d^2 -1 d ---- q(t) = M(q(t)) (F(u(t)) + G(q(t)) + H(-- q(t), q(t))) dt^2 dt
状態を次のように導入します。
、土台とアーム 1 の間の相対角度。
、アーム 1 とアーム 2 の間の相対角度。
、アーム 2 とアーム 3 の間の相対角度。
、土台とアーム 1 の間の相対速度。
、アーム 1 とアーム 2 の間の相対速度。
、アーム 2 とアーム 3 の間の相対速度。
IDNLGREY モデリングに適した、状態空間モデル構造が得られます。まとめると、このモデルには 3 つの入力、6 つの状態、3 つの出力、28 の異なるモデル パラメーターまたは定数があります。
IDNLGREY Manutec R3 ロボット モデル オブジェクト
このアプリケーションに開発された C MEX モデル ファイルはきわめて複雑です。詳細の多くを省き、概略のみを提供します。興味のある読者は、robot_c.c で全体像を確認してください。上記の方程式により、28 (= Np) 個の異なるパラメーターまたは定数があるロボット モデルが得られ、論理的な理由で 10 (= Npo) 個の一意の次のパラメーター オブジェクトに入力されます。3 つのスカラー、5 つのベクトル、2 つの行列。状態更新関数 compute_dx には、次の縮小された入力引数リストがあります。
void compute_dx(double *dx, double *x, double *u, double **p)
ここで p には 10 個のパラメーター オブジェクトが格納されます。
g = p[0]、pl = p[5] および Ia1 = p[8] はスカラー。
Fc = p[1]、r = p[2]、Im = p[3]、m = p[4] および L = p[6] は、2 つまたは 3 つのエントリをもつ列ベクトル。
com = p[7] は 2 行 2 列の行列、Ia = p[9] は 4 行 2 列の行列。
スカラーは通常どおり p[0] として参照され (MATLAB ファイルでは p(1))、i 番目のベクトル要素は p[i-1] で参照されます (MATLAB ファイルでは p(i))。C MEX モデル ファイルに渡される行列は、明白な順序で列が相互に積み上げられるという点で異なります。したがって、com(1, 1) は com[0]、com(2, 1) は com[1]、com(1, 2) は com[3]、com(2, 2) は com[3] として参照されます。同様に、Ia の 8 番目の要素は Ia[i] (i = 0、1、...、7) で取得されます。
これにより、compute_dx は次の計算ステップを実行します (ここでは多くの割り当てを省いています)。ステップ A ~ E の目的は、方程式を再構成して、状態を明示的に計算できるようにすることです。
void compute_dx(double *dx, double *x, double *u, double **p)
{
/* Declaration of model parameters and intermediate variables. */
double *g, *Fc, *r, *Im, *m, *pl, *L, *com, *Ia1, *Ia;
double M[3][3]; /* Mass matrix. */
...
/* Retrieve model parameters. */
...
/* A. Components of the symmetric and positive definite mass matrix M(x, p), a 3x3 matrix. */
M[0][0] = Ia1[0] + r[0]*r[0]*Im[0] + com[2]*com[2]*m[1] ...
...
M[2][2] = Ia[4] + r[2]*r[2]*Im[2] + com[3]*com[3]*m[1] + L[1]*L[1]*pl[0];
/* B. Inputs. */
F[0] = Fc[0]*u[0]; ...
/* C. Gravitational forces G. */
G[0] = 0; ...
/* D. Coriolis and centrifugal force components Gamma and forces H. */
Gamma[1] = (Ia[6] - Ia[5] - com[3]*com[3]*m[1] ...
/* E. Compute inverse of M. */
Det = M[0][0]*M[1][1]*M[2][2] + 2*M[0][1]*M[1][2]*M[0][2] ...
/* State equations. */
/* x[0]: Relative angle between fundament and arm 1. */
/* x[1]: Relative angle between arm 1 and arm 2. */
/* x[2]: Relative angle between arm 2 and arm 3. */
/* x[3]: Relative velocity between fundament and arm 1. */
/* x[4]: Relative velocity between arm 1 and arm 2. */
/* x[5]: Relative velocity between arm 2 and arm 3. */
dx[0] = x[3];
dx[1] = x[4];
dx[2] = x[5];
dx[3] = Minv[0][0]*(F[0]+G[0]+H[0]) + Minv[0][1]*(F[1]+G[1]+H[1]) + Minv[0][2]*(F[2]+G[2]+H[2]);
dx[4] = Minv[0][1]*(F[0]+G[0]+H[0]) + Minv[1][1]*(F[1]+G[1]+H[1]) + Minv[1][2]*(F[2]+G[2]+H[2]);
dx[5] = Minv[0][2]*(F[0]+G[0]+H[0]) + Minv[1][2]*(F[1]+G[1]+H[1]) + Minv[2][2]*(F[2]+G[2]+H[2]);
}
出力更新関数 compute_y はかなりシンプルです。
/* Output equations. */
void compute_y(double y[], double x[])
{
/* y[0]: Relative angle between fundament and arm 1. */
/* y[1]: Relative angle between arm 1 and arm 2. */
/* y[2]: Relative angle between arm 2 and arm 3. */
y[0] = x[0];
y[1] = x[1];
y[2] = x[2];
}
C-MEX モデル ファイルの詳細については、「IDNLGREY モデル ファイルの作成」の例を参照してください。
これで、簡略化された Manutec r3 ロボットの移動を反映する IDNLGREY オブジェクトを作成するための十分な知識が得られました。入力の記述から始めます。
InputName = {'Voltage applied to motor moving arm 1'; ...
'Voltage applied to motor moving arm 2'; ...
'Voltage applied to motor moving arm 3'};
InputUnit = {'V'; 'V'; 'V'};次に、6 つの状態を定義します。最初の 3 つは出力です。
StateName = {'\Theta_1'; ... % Relative angle between fundament and arm 1
'\Theta_2'; ... % Relative angle between arm 1 and arm 2
'\Theta_3'; ... % Relative angle between arm 2 and arm 3
'Vel_1'; ... % Relative velocity between fundament and arm 1
'Vel_2'; ... % Relative velocity between arm 1 and arm 2
'Vel_3'... % Relative velocity between arm 2 and arm 3
};
StateUnit = {'rad'; 'rad'; 'rad'; 'rad/s'; 'rad/s'; 'rad/s'};
OutputName = StateName(1:3);
OutputUnit = StateUnit(1:3);前述したように、モデルには 28 個の異なるパラメーターまたは定数があり、次のように 10 個のパラメーター オブジェクトにまとめられます。一部のパラメーターは物理的な理由から、独自の最小値が指定されています。これらの最小パラメーター値は、パラメーター値の指定に使用されたものと同じサイズの要素の cell 配列で定義されます。
ParName = {'Gravity constant'; ... % g, scalar.
'Voltage-force constant of motor'; ... % Fc, 3-by-1 vector, for motor 1, 2, 3.
'Gear ratio of motor'; ... % r, 3-by-1 vector, for motor 1, 2, 3.
'Moment of inertia of motor'; ... % Im, 3-by-1 vector, for motor 1, 2, 3.
'Mass of arm 2 and 3 (incl. tool)'; ... % m, 2-by-1 vector, for arm 2 and 3.
'Point mass of payload'; ... % pl, scalar.
'Length of arm 2 and 3 (incl. tool)'; ... % L, 2-by-1 vector, for arm 2 and 3.
'Center of mass coordinates of arm 2 and 3'; ... % com, 2-by-2 matrix, 1:st column for arm 2 (x-,z-coord), 2:nd for arm 3.
'Moment of inertia arm 1, element (3,3)'; ... % Ia1, scalar.
'Moment of inertia arm 2 and 3' ... % Ia, 4-by-2 matrix. 1:st column for arm 2, 2:nd for arm 3;
... % column elements: 1: (1,1); 2: (2,2); 3: (3,3); 4: (1,3) and (3,1).
};
ParUnit = {'m/s^2'; 'N*m/V'; ''; 'kg*m^2'; 'kg'; 'kg'; 'm'; 'm'; 'kg*m^2'; 'kg*m^2'};
ParValue = {9.81; [-126; 252; 72]; [-105; 210; 60]; [1.3e-3; 1.3e-3; 1.3e-3]; ...
[56.5; 60.3]; 10; [0.5; 0.98]; [0.172 0.028; 0.205 0.202]; ...
1.16; [2.58 11.0; 2.73 8.0; 0.64 0.80; -0.46 0.50]};
ParMin = {eps(0); -Inf(3, 1); -Inf(3, 1); eps(0)*ones(3, 1); [40; 40]; ...
eps(0); eps(0)*ones(2, 1); eps(0)*ones(2); -Inf; -Inf(4, 2)};
ParMax = Inf; % No maximum constraint.モデル ファイルや初期状態などを指定した後、Manutec r3 IDNLGREY モデル オブジェクトは次のように作成されます。
FileName = 'robot_c'; % File describing the model structure. Order = [3 3 6]; % Model orders [ny nu nx]. Parameters = struct('Name', ParName, 'Unit', ParUnit, 'Value', ParValue, ... 'Minimum', ParMin, 'Maximum', ParMax, 'Fixed', false); InitialStates = struct('Name', StateName, 'Unit', StateUnit, 'Value', 0, ... 'Minimum', -Inf, 'Maximum', Inf, 'Fixed', true); Ts = 0; % Time-continuous system. nlgr = idnlgrey(FileName, Order, Parameters, InitialStates, Ts, ... 'Name', 'Manutec r3 robot', 'InputName', InputName, ... 'InputUnit', InputUnit, 'OutputName', OutputName, ... 'OutputUnit', OutputUnit, 'TimeUnit', 's');
入出力データ
次に、使用できる入出力データを読み込みます。出力は、上記のIDNLGREY モデル構造を使用してシミュレートされています。保存する前に、出力は一部のノイズにより破損しました。
load('robotdata');ファイルには 2 つの異なる (シミュレーションの) 実験から得られたデータが含まれ、それぞれサンプリング レート (Ts) 0.02 秒を使用して生成された入出力サンプルが 101 個含まれています。初期状態ゼロから始めて、実験に使用された 3 つのモーターへの入力 [V] はすべて定数に維持されていました。
u(t) = [u_1(t) u_2(t) u_3(t)]^T = [0.20 0.05 0.03]^T % Experiment 1. u(t) = [u_1(t) u_2(t) u_3(t)]^T = -[0.20 0.05 0.03]^T % Experiment 2.
生成された出力には、上記の記述に従ってデータが保持されます。このモデル化の目的のため、2 つの実験から得られたデータをもつ 1 つの IDDATA オブジェクト z を作成します。
z = merge(iddata(y1, u1, 0.02), iddata(y2, u2, 0.02)); z.Name = 'Manutec r3 robot'; z.InputName = nlgr.InputName; z.InputUnit = nlgr.InputUnit; z.OutputName = nlgr.OutputName; z.OutputUnit = nlgr.OutputUnit; z.Tstart = 0; z.TimeUnit = 's';
初期 Manutec R3 ロボット モデルの性能
パラメーター推定に進む前に、初期パラメーター値を使用してモデルをシミュレートします。既定の微分方程式ソルバー (ode45) を、既定の設定で使用されるよりは相対精度が高い要件で使用します。シミュレーションの出力と実出力がプロット ウィンドウに表示され、示されるように一致は改善されています (3 番目の出力である、アーム 2 とアーム 3 の間の相対角度の実際の値とシミュレーションの値は除く)
nlgr.SimulationOptions.RelTol = 1e-5; compare(z, nlgr);
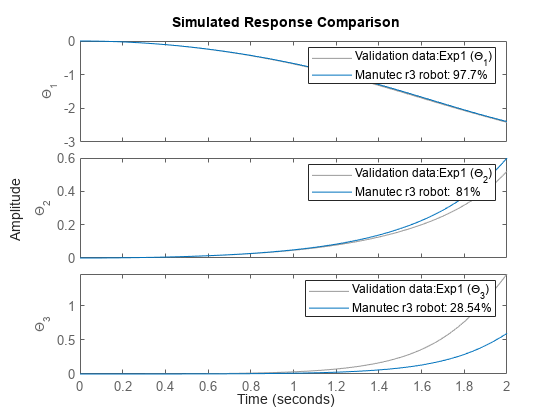
図 2: 初期の Manutec r3 ロボット モデルの実際の出力とシミュレーションの出力の比較
パラメーター推定
Manutec r3 パラメーターの同定は非常に困難です。その理由の一部は、使用できるデータは励起の点で限定されており、ロボット ダイナミクスは非線形であるためです。タスクを簡略化するため、最後の 4 つのパラメーターのみを推定します。これは、アーム 3 とツールに関連する慣性モーメントです。
for k = 1:size(nlgr, 'Npo')-1 % Fix all parameters of the first 9 parameter objects. nlgr.Parameters(k).Fixed = true; end nlgr.Parameters(end).Fixed(:, 1) = true; % Fix the moment of inertia parameters for arm 2.
ここでは Levenberg-Marquardt 探索アルゴリズムを使用します。
opt = nlgreyestOptions('SearchMethod', 'lm', 'Display', 'on'); nlgr = nlgreyest(z, nlgr, opt);
推定された Manutec R3 ロボット モデルの性能
次に、推定された Manutec r3 ロボットの性能をシミュレーションによって調べます。
compare(z, nlgr);
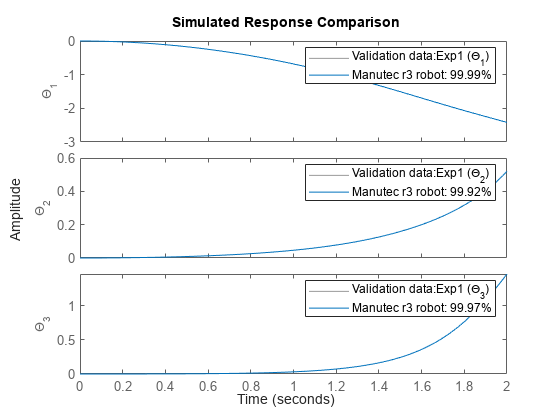
図 3: 推定された Manutec r3 ロボット モデルの実際の出力とシミュレーションの出力の比較
図からわかるように、シミュレーションの出力と実出力との一致は大幅に改善され、特に 3 番目の出力については顕著です (アーム 2 とアーム 3 の間の相対角度)。実パラメーターと推定されたパラメーターは互いに似通っています。
disp(' True Estimated parameter vector');True Estimated parameter vector
ptrue = [9.81; -126; 252; 72; -105; 210; 60; 1.3e-3; 1.3e-3; 1.3e-3; ... 56.5; 60.3; 10; 0.5; 0.98; 0.172; 0.205; 0.028; 0.202; 1.16; ... 2.58; 2.73; 0.64; -0.46; 5.41; 5.60; 0.39; 0.33]; fprintf(' %1.3f %1.3f\n', ptrue(25), nlgr.Parameters(end).Value(1, 2));
5.410 5.414
fprintf(' %1.3f %1.3f\n', ptrue(26), nlgr.Parameters(end).Value(2, 2));5.600 5.609
fprintf(' %1.3f %1.3f\n', ptrue(27), nlgr.Parameters(end).Value(3, 2));0.390 0.390
fprintf(' %1.3f %1.3f\n', ptrue(28), nlgr.Parameters(end).Value(4, 2));0.330 0.331
推定された Manutec r3 ロボット モデルを、PRESENT コマンドでさらに調べてみます。
present(nlgr);
nlgr =
Continuous-time nonlinear grey-box model defined by 'robot_c' (MEX-file):
dx/dt = F(t, u(t), x(t), p1, ..., p10)
y(t) = H(t, u(t), x(t), p1, ..., p10) + e(t)
with 3 input(s), 6 state(s), 3 output(s), and 4 free parameter(s) (out of 28).
Inputs:
u(1) Voltage applied to motor moving arm 1(t) [V]
u(2) Voltage applied to motor moving arm 2(t) [V]
u(3) Voltage applied to motor moving arm 3(t) [V]
States: Initial value
x(1) \Theta_1(t) [rad] xinit@exp1 0 (fixed) in [-Inf, Inf]
xinit@exp2 0 (fixed) in [-Inf, Inf]
x(2) \Theta_2(t) [rad] xinit@exp1 0 (fixed) in [-Inf, Inf]
xinit@exp2 0 (fixed) in [-Inf, Inf]
x(3) \Theta_3(t) [rad] xinit@exp1 0 (fixed) in [-Inf, Inf]
xinit@exp2 0 (fixed) in [-Inf, Inf]
x(4) Vel_1(t) [rad/s] xinit@exp1 0 (fixed) in [-Inf, Inf]
xinit@exp2 0 (fixed) in [-Inf, Inf]
x(5) Vel_2(t) [rad/s] xinit@exp1 0 (fixed) in [-Inf, Inf]
xinit@exp2 0 (fixed) in [-Inf, Inf]
x(6) Vel_3(t) [rad/s] xinit@exp1 0 (fixed) in [-Inf, Inf]
xinit@exp2 0 (fixed) in [-Inf, Inf]
Outputs:
y(1) \Theta_1(t) [rad]
y(2) \Theta_2(t) [rad]
y(3) \Theta_3(t) [rad]
Parameters: Value Standard Deviation
p1 Gravity constant [m/s^2] 9.81 0 (fixed) in ]0, Inf]
p2(1) Voltage-force constant of motor [N*m/V] -126 0 (fixed) in [-Inf, Inf]
p2(2) 252 0 (fixed) in [-Inf, Inf]
p2(3) 72 0 (fixed) in [-Inf, Inf]
p3(1) Gear ratio of motor -105 0 (fixed) in [-Inf, Inf]
p3(2) 210 0 (fixed) in [-Inf, Inf]
p3(3) 60 0 (fixed) in [-Inf, Inf]
p4(1) Moment of inertia of motor [kg*m^2] 0.0013 0 (fixed) in ]0, Inf]
p4(2) 0.0013 0 (fixed) in ]0, Inf]
p4(3) 0.0013 0 (fixed) in ]0, Inf]
p5(1) Mass of arm 2 and 3 (incl. tool) [kg] 56.5 0 (fixed) in [40, Inf]
p5(2) 60.3 0 (fixed) in [40, Inf]
p6 Point mass of payload [kg] 10 0 (fixed) in ]0, Inf]
p7(1) Length of arm 2 and 3 (incl. tool) [m] 0.5 0 (fixed) in ]0, Inf]
p7(2) 0.98 0 (fixed) in ]0, Inf]
p8(1,1) Center of mass coordinates of arm 2 and 3 [m] 0.172 0 (fixed) in ]0, Inf]
p8(2,1) 0.205 0 (fixed) in ]0, Inf]
p8(1,2) 0.028 0 (fixed) in ]0, Inf]
p8(2,2) 0.202 0 (fixed) in ]0, Inf]
p9 Moment of inertia arm 1, element (3,3) [kg*m^2] 1.16 0 (fixed) in [-Inf, Inf]
p10(1,1) Moment of inertia arm 2 and 3 [kg*m^2] 2.58 0 (fixed) in [-Inf, Inf]
p10(2,1) 2.73 0 (fixed) in [-Inf, Inf]
p10(3,1) 0.64 0 (fixed) in [-Inf, Inf]
p10(4,1) -0.46 0 (fixed) in [-Inf, Inf]
p10(1,2) 5.41371 1.80292e-11 (estimated) in [-Inf, Inf]
p10(2,2) 5.60905 7.67168e-11 (estimated) in [-Inf, Inf]
p10(3,2) 0.389978 1.58707e-12 (estimated) in [-Inf, Inf]
p10(4,2) 0.330506 2.25628e-12 (estimated) in [-Inf, Inf]
Name: Manutec r3 robot
Status:
Termination condition: Near (local) minimum, (norm(g) < tol)..
Number of iterations: 10, Number of function evaluations: 49
Estimated using Solver: ode45; Search: lm on time domain data "Manutec r3 robot".
Fit to estimation data: [99.99 99.99;99.92 99.93;99.97 99.97]%
FPE: 9.788e-25, MSE: [2.821e-08 3.086e-08]
More information in model's "Report" property.
Model Properties
一部の同定結果
この場合、実パラメーターに非常に近いパラメーターが得られます。ただし、一般には、実パラメーターが見つからない理由がいくつかあります。
使用可能なデータの "情報が不十分" なため、パラメーターを同定できない (データが持続的に励起していない)。
ノイズが多いためにデータが破損していて、実パラメーターを見つけることが事実上不可能。
ローカルかつ検索対象ではない大域的最小値が見つかった。このリスクは、反復探索アルゴリズムを使用している場合は常に存在します。
モデル構造のパラメーターが一意に同定可能ではない。一般的には、推定されるパラメーターが多い場合に、このリスクが大きくなります (たとえば、Manutec r3 ロボットの 28 個のパラメーターすべてを推定すると、通常は物理的に不可能なパラメーター値になります)。
モデル構造が単に "複雑すぎる" か、"滑らかさが十分でない" 非線形性が含まれている。
まとめ
このチュートリアルの主な目的は、IDNLGREY C MEX モデリング フレームワークにベクトルまたは行列であるパラメーターを含める方法を説明しました。また、ロボット モデリングの例について実施し、要求される明示的な状態空間フォームに一致させるために方程式を操作しました。
