正規化された LMS 適応フィルターを使用した、Simulink での低周波ノイズの除去

適応フィルターは、システムの動的性質を追うことから、時間とともに変化する信号の除去を可能にします。DSP System Toolbox™ ライブラリには最小平均二乗 (LMS)、ブロック LMS、高速ブロック LMS、および逐次最小二乗 (RLS) の適応フィルターアルゴリズムを実装するためのブロックがあります。これらのフィルターは、そのフィルター係数を変えることにより出力信号と要求される信号との差を縮めます。時間とともに、適応フィルターの出力信号は再現しようとする信号によりいっそう近づきます。

Simulink での適応フィルターの設計

この例では次を使用します。

ライブスクリプトを開く

この例では、LMS 適応フィルターを設計して信号内の低周波ノイズを取り除きます。

モデルにデジタルフィルターを追加するで作成したモデルがデスクトップ上に開いていない場合は、同等のモデルである ex_gstut5 を開きます。

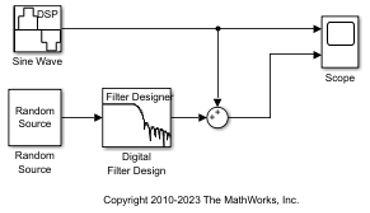
MATLAB® コマンドプロンプトで dsplib と入力して、DSP System Toolbox™ ライブラリを開きます。

LMS Filterブロックをシステムに追加して低周波ノイズを信号から取り除きます。これは、飛行機のシナリオでコックピット内のマイクへの入力から風切音を差し引くことに相当します。Filtering ライブラリをダブルクリックし、それから Adaptive Filters ライブラリをダブルクリックします。LMS Filter ブロックをモデルに追加します。

Digital Filter Design ブロックの出力をモデル化するように LMS Filter ブロックのパラメーターを設定します。ブロックをダブルクリックして [LMS フィルター] ダイアログボックスを開きます。ブロックパラメーターを以下のように設定して適用します。

アルゴリズム = Normalized LMS
フィルター長 = 32
ステップサイズの指定方法 = Dialog
ステップサイズ (mu) = 0.1
漏れ係数 (0 ～ 1) = 1.0
フィルターの重みの初期値 = 0
[Adapt 端子] チェックボックスをオフにする。
リセット端子 = None
[フィルターの重みの出力] チェックボックスをオンにする。

これらのパラメーターに基づき、LMS Filter ブロックは正規化 LMS 法の式を使い、フィルターの重みを計算します。指定したフィルター次数は Digital Filter Design ブロックのものと同じです。[ステップサイズ (mu)] パラメーターはフィルター更新ステップの細かさを定義します。[漏れ係数 (0 ～ 1)] パラメーターを 1.0 に設定したので、現在のフィルター係数の値はフィルターの初期条件およびこれまでの入力値に影響されます。フィルターの重み (係数) の初期値は 0 です。[フィルターの重みの出力] チェックボックスをオンにしたので、[Wts] 端子がブロックに表示されます。この端子からフィルターの重みが出力されます。

LMS Filter ブロックのパラメーター設定が完了しました。ブロック線図にこのブロックを組み込めます。

モデルに適応フィルターを追加する

この例では次を使用します。

ライブスクリプトを開く

この例では、Simulink での適応フィルターの設計で設計した適応フィルターをシステムに組み込んで元の正弦波信号を取り出します。飛行機のシナリオにおいて、この適応フィルターはコックピット内で聞こえる低周波ノイズをモデル化しています。その結果、マイクへの入力がパイロットの声だけとなるようにノイズを除去することができます。

Simulink での適応フィルターの設計で作成したモデルがデスクトップ上に開いていない場合は、同等のモデルである ex_gstut6 を開きます。

モデルに Sum ブロックを追加して、低周波ノイズを含んだ正弦波から適応フィルターの出力を減算します。tm_simulink Math Operations ライブラリの Simulink フォールバックから Sum ブロックをモデルにドラッグします。このブロックをダブルクリックして Sum ダイアログボックスを開きます。[符号リスト] パラメーターを |+- に変更して [OK] をクリックします。

システムに LMS Filter ブロックを組み込みます。

Random Source ブロックの出力を LMS Filter ブロックの [Input] 端子に接続します。飛行機のシナリオでは、ランダムノイズは飛行機の外にあるセンサーで計測されたホワイトノイズに相当します。LMS Filter ブロックは機体がノイズに及ぼす影響をモデル化したものです。
Digital Filter Design ブロックの出力を LMS Filter ブロックの [Desired] 端子に接続します。これが LMS ブロックで再現しようとする信号です。
LMS Filter ブロックの出力を手順 2 で追加した Sum ブロックのマイナス端子に接続します。
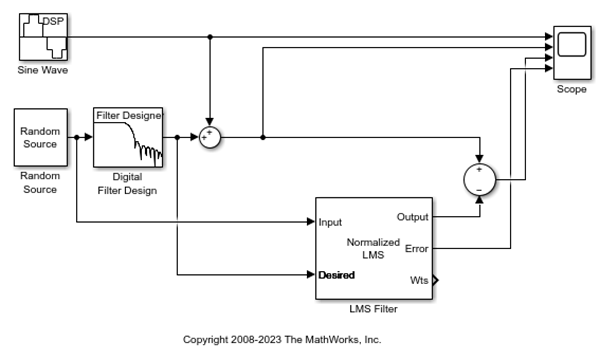
1 番目の Sum ブロックの出力を 2 番目の Sum ブロックのプラス端子に接続します。モデルは次の図のようになっているはずです。

2 番目の Sum ブロックへのプラス入力は、入力信号と低周波ノイズの合計 s(n) + y です。2 番目の Sum ブロックへのマイナス入力は、LMS Filter ブロックによる低周波ノイズの最良推定値 y' です。これらの 2 つの信号を減算すると、入力信号の近似値が残ります。

${s (n)}_{approx} = s (n) + y - y^{'}$

この方程式は、以下を意味します。

$s (n)$ は入力信号。
${s (n)}_{approx}$ は入力信号の近似値。
$y$ は、Random Source ブロックと Digital Filter Design ブロックによって作成されるノイズ。
$y^{'}$ は LMS Filter ブロックによるノイズの近似値。

LMS Filter ブロックではノイズの近似のみが可能であり、入力信号と入力信号の近似値との間には違いが存在します。続くステップでは、本来の正弦波信号とその近似値を比較できるように Scope ブロックを設定します。

Scope ブロックに入力と軸を 2 つずつ追加します。Scope ブロックをダブルクリックして、[Scope] ダイアログボックスを開きます。[パラメーター] ボタンをクリックします。[座標軸数] パラメーターに 4 と入力します。[OK] をクリックしてダイアログボックスを閉じます。

新しい Scope 軸にラベルを付けます。Scope ウィンドウで、3 番目の軸を右クリックし、[座標軸プロパティ] を選択します。[Scope プロパティ: 軸 3 ] ダイアログボックスが開きます。[タイトル] ボックスに Approximation of Input Signal と入力します。[OK] をクリックしてダイアログボックスを閉じます。4 番目の軸にも同じ手順を繰り返し、「Error」とラベルを付けてください。

2 番目の Sum ブロックの出力を Scope ブロックの 3 番目の端子に接続します。

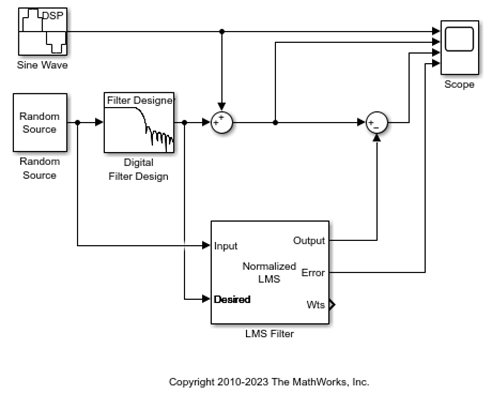
LMS Filter ブロックの [Error] 端子の出力を Scope ブロックの 4 番目の端子に接続します。モデルは次の図のようになっているはずです。

この例では、[Error] 端子からの出力は LMS Filter に要求された信号とその出力信号の差です。誤差がゼロになることはないため、フィルターは低周波ノイズにより近づくためにフィルター係数を変更し続けます。近似すればするほど、正弦波信号から低周波ノイズを取り除くことができます。次のトピック適応フィルター係数を表示では時間経過に応じた適応フィルター係数の変化の表示方法を学びます。

適応フィルター係数を表示

この例では次を使用します。

ライブスクリプトを開く

適応フィルターの係数は選択されたアルゴリズムに従って時間とともに変化します。アルゴリズムがフィルターのパフォーマンスを最適化すると、これらのフィルター係数は定常値に達します。シミュレーションの実行中に係数の変化を表示して、係数が定常値に落ち着くのを見ることができます。これにより、実際のシステムにそれらの値を適用できるかどうかを判断することができます。

モデルに適応フィルターを追加するで作成したモデルがデスクトップ上に開いていない場合は、同等のモデルである ex_gstut7 を開きます。

適応フィルターの [Wts] 端子 (フィルターの重みを出力) がまだ接続されていないということを念頭においてください。

MATLAB® コマンドプロンプトで dsplib と入力して、DSP System Toolbox™ ライブラリを開きます。

Time Scopeブロックを LMS Filter ブロックの [Wts] 端子に接続して、フィルター係数を表示します。

Time Scope ブロックで、次のコンフィギュレーションプロパティを変更します。

時間範囲 = 0.05
Y 軸範囲 (最小) = -0.15
Y 軸範囲 (最大) = 0.5

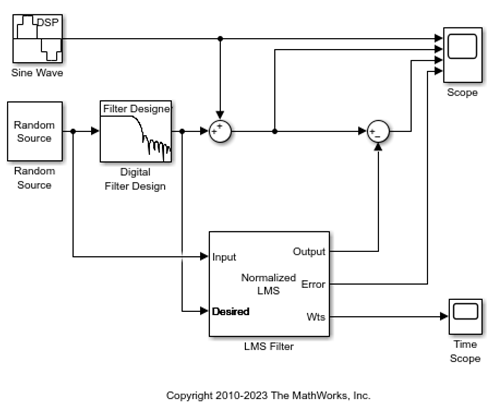
[モデル設定] を開きます。[モデル化] タブの [モデル設定] をクリックします。[ソルバー] ペインで、次のコンフィギュレーションパラメーターを設定します。

終了時間 = inf
タイプ = Fixed-step
ソルバー = discrete (no continuous states)

DSP System Toolbox ブロックを含むモデルには、このコンフィギュレーションパラメーターを使用することを推奨します。これらのブロックは、微分方程式を解くよりもむしろ値を直接計算することから、Simulink® ソルバーがスケジューラのように振る舞うよう設定する必要があります。ソルバーは、スケジューラモードの場合、ブロックのサンプル時間を使用してそれぞれのブロックの背後にあるコードが実行されるタイミングを決定します。たとえば、このモデルの Sine Wave ブロックと Random Source ブロックのサンプル時間は 0.05 です。ソルバーはこれらのブロックおよび同じサンプル時間をもつ他のブロックの背後にあるコードを 0.05 秒ごとに実行します。

メモ: DSP System Toolbox のブロックを含むモデルを使用する際には、それらのサンプル時間を指定できるソースブロックを使用してください。ソースブロックに [サンプル時間] パラメーターがない場合、Zero-Order Hold ブロックをモデルに追加してサンプル時間を指定しなければなりません。詳細については、連続時間ソースブロックを参照してください。ただし、これは Constant ブロックには当てはまりません。このブロックは定数サンプル時間をもつことができます。その場合、Simulink はこのブロックを実行して、定数をシミュレーション開始時に 1 回記録し、さらにパラメーターを調整した際にも毎回記録します。これにより、シミュレーションの高速化とよりコンパクトなコードの生成が可能になります。

モデルを実行して Time Scope (シミュレーションが始まると自動的に開きます) でフィルター係数の挙動を確認します。時間の経過とともにフィルター係数が定常値に近づきます。

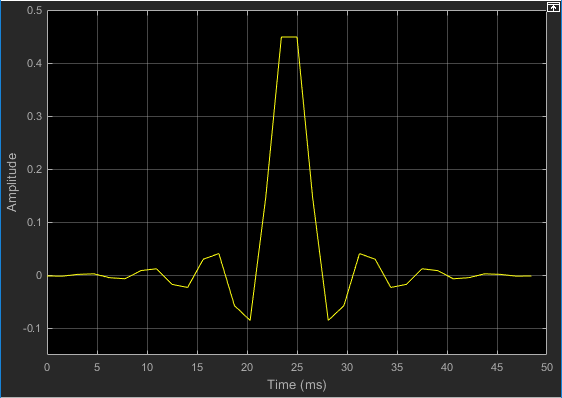
また、システムの挙動を Scope ウィンドウで見ることができます。時間の経過とともに、誤差が減少し、入力信号の近似値が本来の正弦波入力信号に近づいていくのがわかります。

これで、適応ノイズキャンセリングを行うモデルが完成しました。

まとめ

Digital Filter Design ブロックを使用してローパスフィルターを設計する方法を学びました。また、LMS Filter ブロックを使用して適応フィルターを作成する方法も学びました。DSP System Toolbox 製品には他にもデジタルフィルターおよび適応フィルターを設計し実装するためのブロックが含まれます。この製品のフィルター処理機能の詳細については、フィルターの設計およびフィルター解析を参照してください。

このモデルではすべてのブロックのサンプル時間は同一であるため、このモデルはシングルレートであり Simulink^® はこれを [SingleTasking] ソルバーモードで実行しました。モデル内のブロックにサンプル時間が異なるものがある場合、そのモデルはマルチレートになるため Simulink はそれを [MultiTasking] ソルバーモードで実行する場合があります。ソルバーモードの詳細については、離散時間シミュレーション用の推奨設定を参照してください。

Simulink Coder™ 製品を使用してモデルからコードを生成する方法については、Simulink モデルからの C コードの生成を参照してください。

参考

LMS Filter | Digital Filter Design