このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
Overlap-Add/Overlap-Save
この例では、Frequency-Domain FIR フィルター ブロックを使用して、オーバーラップ加算およびオーバーラップ保存 FFT 手法で正弦波をフィルター処理する方法を示します。
オーバーラップ加算
オーバーラップ加算アルゴリズム[1]は、周波数領域の入力信号をフィルター処理します。入力はオーバーラップしないブロックに分割され、それらのブロックには FIR フィルター係数で線形畳み込みが行われます。各ブロックの線形畳み込みは、ブロックの離散フーリエ変換 (DFT) とフィルター係数を乗算し、積の逆 DFT を計算して求めます。フィルター長が M、FFT サイズが N の場合、線形畳み込みの最後の M-1 サンプルは次の入力シーケンスの最初の M-1 サンプルに追加されます。各総和結果の最初の N-M+1 サンプルは、連続した出力になります。
オーバーラップ保存
オーバーラップ保存アルゴリズム[2]も、周波数領域の入力信号をフィルター処理します。入力はオーバーラップするブロックに分割され、それらのブロックには FIR フィルター係数で循環畳み込みが行われます。各ブロックの循環畳み込みは、ブロックの DFT とフィルター係数を乗算し、積の逆 DFT を計算して求めます。フィルター長が M、FFT サイズが N の場合、循環畳み込みの最初の M-1 点は無効となり、破棄されます。出力は、実際の畳み込みと同様に残りの N-M+1 点で構成されます。
レイテンシ
オーバーラップ保存およびオーバーラップ加算では、N-M+1 サンプルの処理レイテンシが生じます。分子を短いセグメントに分割して各区画にオーバーラップ加算またはオーバーラップ保存を適用し、結果を結合してフィルター処理された出力を得ることで、このレイテンシは削減できます[3]。レイテンシは分割の長さにまで減少しますが、その代わり従来のオーバーラップ保存またはオーバーラップ加算と比べて追加の計算が必要になります (それでも長いフィルターの時間領域のフィルター処理よりも計算は効率的です)。
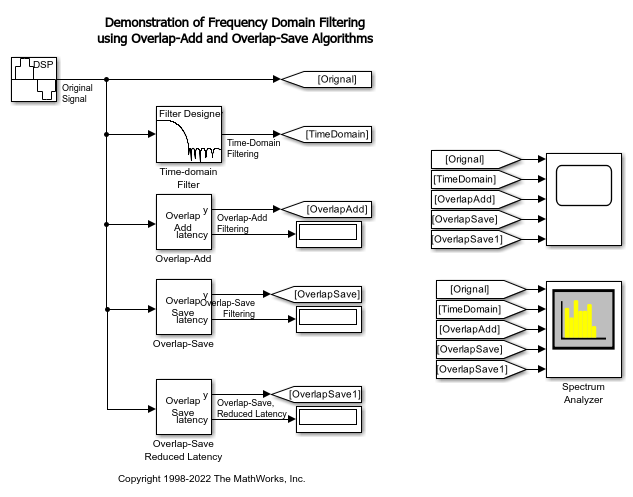
オーバーラップ加算およびオーバーラップ保存モデル
このモデルは、500 Hz の正弦波を時間領域と周波数領域でフィルター処理した結果を示します。このモデルをシミュレートすると、元の信号とフィルター処理された信号はどちらも時間領域と周波数領域でプロットされます。
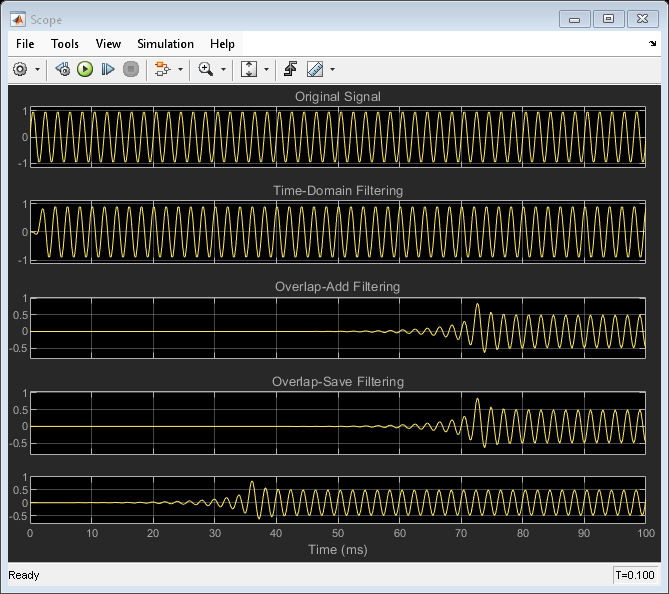
結果
スコープの最初のプロットには元の入力信号が表示されます。2 番目のプロットには、従来の時間領域フィルター処理を使用してフィルター処理された信号が表示され、レイテンシは最も小さくなっています。3 番目と 4 番目のプロットには、オーバーラップ加算とオーバーラップ保存の周波数領域フィルター処理手法でフィルター処理された信号が表示されます。どちらの手法も処理レイテンシは同じ 213 サンプルです。5 番目のプロットには、オーバーラップ保存手法を使用してフィルター処理された信号が表示されます。現在、オーバーラップ保存手法の分割の長さが 30 のため、フィルター処理された信号は 30 サンプルのレイテンシを示しています。この分割の値は、元の分割の長さである 213 サンプルより小さくなります。
Spectrum Analyzer ブロックは、元の信号とフィルター処理された信号を周波数領域で表示します。

参照
[1] Overlap-Add Algorithm: Proakis and Manolakis, Digital Signal Processing, 3rd ed, Prentice-Hall, Englewood Cliffs, NJ, 1996, pp. 430 - 433.
[2] Overlap-Save Algorithm: Oppenheim and Schafer, Discrete-Time Signal Processing, Prentice-Hall, Englewood Cliffs, NJ, 1989, pp. 558 - 560.
[3] T. G. Stockham Jr., "High-speed convolution and correlation", Proc. 1966 Spring Joint Computer Conf., AFIPS, Vol 28, 1966, pp. 229-233.
参考
Sine Wave | Frequency-Domain FIR Filter | Spectrum Analyzer | Scope (Simulink)
