allmargin

ゲイン余裕、位相余裕、遅延余裕、および交差周波数

構文

S = allmargin(L)

S = allmargin(mag,phase,w,ts)

説明

S = allmargin(L) は、開ループ応答 L をもつ SISO または MIMO の負のフィードバック ループについてゲイン余裕、位相余裕、遅延余裕、および対応する交差周波数を計算します。負のフィードバック ループは feedback(L,eye(M)) として計算され、ここで M は L 内の入力と出力の数です。

MIMO システムの場合、allmargin は、負のフィードバックの閉ループ システムについての一度に 1 ループごとの安定余裕を返します。allmargin を使用して、遅延のあるモデルを含む任意の SISO または MIMO モデルの従来の余裕を見つけます。

S = allmargin(mag,phase,w,ts) は、周波数応答データ mag、phase、w およびサンプル時間 ts から安定余裕を計算します。

例

伝達関数の安定余裕

この例では、次で与えられる SISO 開ループ伝達関数 L について考えます。

$$L=\frac{25}{s^3+10s^2+10s+10}$$

L = tf(25,[1 10 10 10]);

L の安定余裕を求めます。

S = allmargin(L)

S = struct with fields:
     GainMargin: 3.6000
    GMFrequency: 3.1623
    PhaseMargin: 29.1104
    PMFrequency: 1.7844
    DelayMargin: 0.2847
    DMFrequency: 1.7844
         Stable: 1

出力 S は、L の負のフィードバック ループの従来の余裕と、そのそれぞれの交差周波数をもつ構造体です。

MIMO システムの安定余裕

この例では、2 つの入力と 2 つの出力をもつ MIMO 状態空間モデル L について考えます。

データを読み込みます。

load('mimoStateSpaceModel.mat','L')

MIMO システムの従来の余裕を見つけます。

S = allmargin(L)

S=2×1 struct array with fields:
    GainMargin
    GMFrequency
    PhaseMargin
    PMFrequency
    DelayMargin
    DMFrequency
    Stable

出力 S は、従来の余裕とそのそれぞれの交差周波数からなる 2 行 1 列の構造体配列です。たとえば、S(1) は、他のループがすべて閉じた状態の最初の I/O フィードバック チャネルの安定余裕を参照します。

配列内のモデルの安定余裕

この例では、倒立振子 SISO モデルを含む 3 行 3 列の配列が格納された invertedPendulumArray.mat を読み込みます。振子の質量は sys の単一の列に沿ってモデル間を移動するにつれて変化し、振子の長さは単一の行に沿って移動するにつれて変化します。質量の値には 100g、200g、300g、振子の長さには 3m、2m、1m がそれぞれ使用されます。

$$\begin{array}{cccc}& Column1& Column2& Column3\\ Row1& 100g,3m& 100g,2m& 100g,1m\\ Row2& 200g,3m& 200g,2m& 200g,1m\\ Row3& 300g,3m& 300g,2m& 300g,1m\end{array}$$

load('invertedPendulumArray.mat','sys');
size(sys)

3x3 array of transfer functions.
Each model has 1 outputs and 1 inputs.

配列内のすべてのモデルの安定余裕を見つけます。

S = allmargin(sys)

S=3×3 struct array with fields:
    GainMargin
    GMFrequency
    PhaseMargin
    PMFrequency
    DelayMargin
    DMFrequency
    Stable

allmargin は、3 行 3 列の構造体配列 S を返します。各エントリは、sys の対応するエントリの安定余裕を含む構造体です。たとえば、重さ 100g、長さ 2m の振子のモデルの安定余裕は S(1,2) に格納されます。

周波数応答データからの安定余裕

この例では、w の周波数で測定されたゲイン m と位相値 p で構成される開ループ システムの周波数応答データを読み込みます。

load('openLoopFRData.mat','m','p','w','ts');

周波数応答データを使用して安定余裕を計算します。

S = allmargin(m,p,w,ts)

S = struct with fields:
     GainMargin: 0.6249
    GMFrequency: 1.2732
    PhaseMargin: [-90.0000 48.9853]
    PMFrequency: [1.0000 1.5197]
    DelayMargin: [4.7124 0.5626]
    DMFrequency: [1.0000 1.5197]
         Stable: NaN

出力 S は、従来の余裕とそのそれぞれの交差周波数をもつ構造体です。allmargin は周波数応答データ モデルの安定性を評価することができないため、S.Stable = NaN となります。

入力引数

L — 開ループ応答

動的システムのモデル | モデル配列

開ループ応答。動的システム モデルとして指定します。L は、入力数と出力数が同じであれば SISO または MIMO にできます。allmargin は、負のフィードバックの閉ループ システム feedback(L,eye(M)) の従来の安定余裕を計算します。

正のフィードバック システム feedback(L,eye(M),+1) の安定余裕を計算するには、allmargin(-L) を使用します。

コントローラー P とプラント C がある場合、プラントの入力または出力におけるゲインと位相の変動についての安定余裕を計算できます。次のブロック線図について考えます。

• プラント出力における余裕を計算するには、L = P*C と設定します。

• プラント入力における余裕を計算するには、L = C*P と設定します。

L は連続時間または離散時間にできます。L が一般化状態空間モデル (genss または uss) の場合、allmargin は L 内のすべての制御設計ブロックの現在の値またはノミナル値を使用します。

L が周波数応答データ モデル (frd など) の場合、allmargin はモデルで表現される各周波数における余裕を計算します。この関数は、最小の安定余裕をもつ周波数の余裕を返します。

L がモデル配列の場合、allmargin は配列内の各モデルの余裕を計算します。

mag — システム応答のゲイン

3 次元配列

絶対単位でのシステム応答のゲイン。3 次元配列として指定します。mag は M x M x N の配列で、M が入力または出力の数、N が周波数点の数です。mag の取得の詳細については、振幅と位相のデータの取得およびMIMO システムの振幅と位相を参照してください。

phase — システム応答の位相

3 次元配列

度単位でのシステム応答の位相。3 次元配列として指定します。phase は M x M x N の配列で、M が入力または出力の数、N が周波数点の数です。phase の取得の詳細については、振幅と位相のデータの取得およびMIMO システムの振幅と位相を参照してください。

w — システム応答のゲイン値と位相値が取得される周波数

列ベクトル

システム応答のゲイン値と位相値が取得される周波数。列ベクトルとして指定します。周波数ベクトル w には任意の単位を指定できます。allmargin は周波数を同じ単位で返します。正確な安定余裕を近似するために、周波数点間で allmargin による内挿が行われます。

ts — サンプル時間

整数

サンプル時間。整数として指定します。allmargin は ts を使用して周波数応答データから安定余裕を見つけます。

• 連続時間モデルの場合、ts = 0 と設定します。

• 離散時間モデルの場合、ts はサンプリング周期を表す正の整数です。指定のないサンプル時間を伴う離散時間モデルを示すには、ts = -1 と設定します。

出力引数

S — ゲイン、位相、および遅延余裕

構造体 | 構造体配列

ゲイン、位相、および遅延余裕。構造体配列として返されます。

出力 S は、以下のフィールドをもつ構造体です。

• GMFrequency: すべての -180° (360°を法とする) の交差周波数 (rad/TimeUnit 単位、TimeUnit は L の TimeUnit プロパティで指定される時間単位)。

• GainMargin: 対応するゲイン余裕 (1/G と定義。G は -180°交差周波数におけるゲイン)。ゲイン余裕は絶対単位です。

• PMFrequency: すべての 0 dB 交差周波数 (rad/TimeUnit 単位、TimeUnit は L の TimeUnit プロパティで指定される時間単位)。

• PhaseMargin: 対応する位相余裕 (度単位)。

• DMFrequency および DelayMargin: DelayMargin はシステムが安定性を失う前に許容できる最大遅延量。DMFrequency は遅延余裕に対応する臨界周波数。遅延余裕は、連続時間システムではシステムの時間単位、離散時間システムではサンプル時間の倍数で指定される。

• Stable: ノミナル閉ループ システムが安定の場合は 1、不安定の場合は 0、安定性を評価できない場合は NaN。一般に、allmargin は frd システムの安定性を評価できません。

L が M 行 M 列の MIMO システムの場合、S は M 行 1 列の構造体配列です。たとえば、S(j) は、ほかのすべてのループが閉じた状態の j 番目のフィードバック チャネルの安定余裕を提供します (一度に 1 ループごとの余裕)。

ヒント

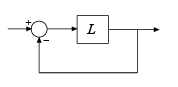
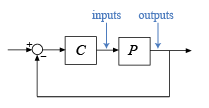
• allmargin は、開ループ応答 L をもつシステムが負のフィードバック システムであると仮定します。正のフィードバック システム feedback(L,eye(M),+1) の従来の安定余裕を計算するには、allmargin(-L) を使用します。

• Simulink^® でモデル化されたシステムの従来の余裕を計算するには、まずモデルを線形化して、特定の操作点における開ループ応答を取得します。その後、allmargin を使用して、線形化されたシステムの従来の安定余裕を計算します。詳細については、Stability Margins of a Simulink Model (Robust Control Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

線形システム アナライザー | margin | diskmargin (Robust Control Toolbox)

トピック

• Stability Margins of a Simulink Model (Robust Control Toolbox)

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい