Programming Patterns: Maximizing Code Performance by Optimizing Memory Access
By Stuart McGarrity, MathWorks
Most MATLAB users want their code to be fast, especially when it is processing very large data sets. Because memory performance has not increased at the same rate as CPU performance, code today is often “memory-bound,” its overall performance limited by the time it takes to access memory.
Fortunately, with a little knowledge of how MATLAB stores and accesses data, you can avoid inefficient memory usage and improve the speed of your code.
This article describes three ways to improve the performance of memory-bound code:
- Preallocate arrays before accessing them within loops
- Store and access data in columns
- Avoid creating unnecessary variables
In each case we will compare the execution speed of a code segment before and after applying the technique. To ensure the best performance, the code segments are all timed in function M-files, not script M-files. As memory performance is machine-dependent, the performance tests were carried out on two different machines1.
Preallocate Arrays Before Accessing them Within Loops
When creating or repeatedly modifying arrays within loops, always allocate the arrays beforehand. Of all three techniques, this familiar one can give the biggest performance improvement.
The code segments in Figure 1 use a for loop to calculate a sequence of numbers based on the equation, x(k) = 1.05* x(k-1), equal to the annual balance of a bank account earning a 5% interest rate.

Why Code Segment 2 is Faster
The MATLAB language does not require you to declare the types and sizes of variables before you use them. As a result, you can increase the size of an array merely by indexing into it at a point larger than the current size. This approach is convenient for quick prototyping of code, but each time you use it, MATLAB must allocate memory for a new larger array and then copy the existing data into it. Code that repeats this procedure several times, as in a loop, is slow and inefficient.
In one step, code segment 2 preallocates the entire array x to the largest size that it needs to be. No more memory allocation is then required during the execution of the code. If the M-Lint code checker finds an opportunity to preallocate, it issues a warning.
Store and Access Data in Columns
When processing 2-D or N-D arrays, access your data in columns and store it so that it is easily accessible by columns.
The code segments in Figure 2 copy the positive values of the 2-D array x to a new array, y.

Why Code Segment 2 is Faster Modern CPUs use a fast cache to reduce the average time taken to access main memory. Your code achieves maximum cache efficiency when it traverses monotonically increasing memory locations. Because MATLAB stores matrix columns in monotonically increasing memory locations, processing data column-wise results in maximum cache efficiency.
Code segment 2 is faster because it traverses the elements of the 2-D array by going down the columns in the inner loop. If the algorithm permits, you can also maximize cache efficiency by using the single index method, x(k), instead of x(r,c).
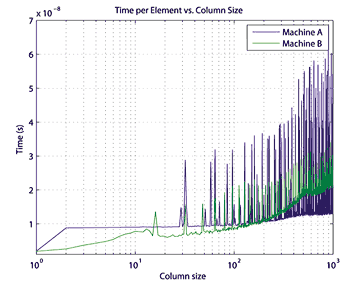
Cache effects are data-size- and machine-dependent, making it difficult to predict performance. For example, column size affects memory access time when you operate on row vectors because it determines the stride, or step through memory. Figure 3 shows the time taken per element on the two machines to perform element-wise multiplication of a 10k element row vector by a matrix of varying column size. The operation is most efficient for a column size equal to 1, a 1-D vector. For other column sizes, code can run up to an order of magnitude more slowly.
Even array size affects efficiency. Figure 4 shows the time taken per element on the two machines to perform element-wise multiplication on a 1-D array of varying size. Depending on the cache and memory characteristics of the computer, processing large arrays is orders of magnitude more efficient than processing small arrays.
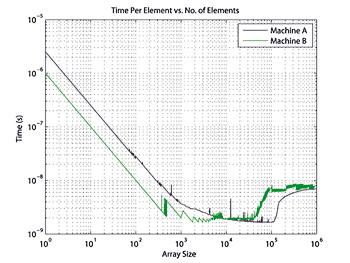
In some cases, the time taken to process arrays that differ slightly in size can vary widely, and optimizing code for a problem size on one machine may not yield the same results on another.
Avoid Creating Unnecessary Variables
When creating new variables or variables that are functions of existing data sets, ensure that they are essential to your algorithm, particularly if your data set is large.
The code segments in Figure 5a and 5b multiply the matrix x, by a scalar via an operator in segments 1 and 2 (Figure 5a), and via an M-function in segments 3 and 4 (Figure 5b).


Why Code Segments 2 and 4 are Faster
In MATLAB, it is easy to inadvertently make copies of your data. For a large data set this uses a lot of memory, and the allocation and copying of memory can itself be time-consuming.
Code segments 2 and 4 are faster because they use in-place operations to avoid creating new variables that are modified versions of the existing ones. This capability is available with element-wise operators (such as .*, +), some MATLAB functions (such as sin and sqrt), and your own M-functions. To create a function M-file that can be called in-place, you must ensure that the output argument matches one of the input arguments. The ability to call functions in-place (introduced in MATLAB 7.3) is available only when the function itself is called from a function M-file and not from a script.
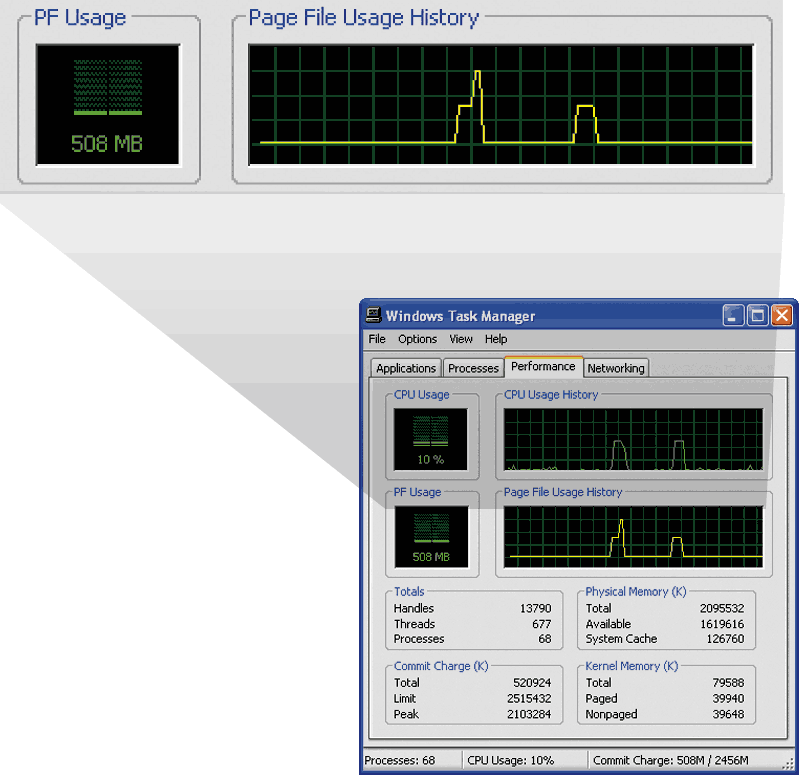
As mentioned earlier, in-place operations result in reduced memory consumption as well as reduced computation time. Figure 6 shows the memory usage in the Windows Task Manager during the execution of code segments 1 and 2 processing a 100-million element array (stepped through manually with the debugger to make memory changes more obvious).
Reduced memory usage is particularly important when dealing with data sets that are larger than the available RAM. Operating systems supplement physical RAM memory with a swap or page file stored on disk. Accessing data stored on disk is orders of magnitude slower than accessing data stored in RAM, however. For maximum performance, keep memory usage low enough to prevent your system from running out of RAM when MATLAB is executing.
Memory Performance Glossary
Cache. The fast memory on a processor or on a motherboard, used to improve the performance of main memory by temporarily storing data.
RAM. Main physical memory, usually in the range of 1GB to 4GB on 32-bit operating systems.
Memory-bound code. Code whose performance is limited by memory speed, not by CPU speed.
Stride. Memory step size taken by the code when accessing matrix rows.
Vectorized code. Code that operates on arrays and does not use for loops.
1 - Machine A is a Lenovo T60 ThinkPad, 1.83GHz Intel Core Duo T2400 processor, 2MB L2 cache, 2GB RAM, 32-bit Windows XP. Machine B is a Dual 2.1GHz AMD Opteron 248 processor machine, 1MB L2 Cache, 1GB RAM, 64-bit Linux.
Published 2007 - 91470v00