Designing a Torque Controller for a PMSM through Simulation on a Virtual Dynamometer
By Dakai Hu, MathWorks
Controlling the torque of a permanent magnet synchronous machine (PMSM) to achieve high levels of accuracy and efficiency is one of the most important targets in high-performance motor drives design. In this article you will learn how simulation performed on a finite element analysis (FEA)-based high-fidelity PMSM machine can help you design motor control algorithms that achieve high torque control accuracy while maximizing the machine’s efficiency.
Motor control engineers commonly use simulation only for algorithm design proof-of-concept studies. These algorithms typically include lookup tables (LUTs) that must be calibrated to achieve the desired performance. Most controller LUTs are obtained by running tests on actual hardware using a dynamometer (dyno). Typically, these include machine validation, characterization, and efficiency tests. While testing on a dyno is the ultimate goal, it can be impractical at times. Several factors need to be considered when it comes to utilizing dyno time―for example, the dyno operation time, operation costs, safety issues, and failures in the machine, the inverter, or the load bank.
Minimizing dyno time is inevitably a high priority for motor control engineers. Model-Based Design helps engineers perform more testing by simulating a “virtual dyno” in Simulink® to reduce hardware testing and overall development time. At a high level, the purpose of performing simulation using the virtual dyno approach is to characterize the PMSM and obtain the machine’s nonlinear flux linkage and torque data, which can then be used to design and implement flux-weakening torque control LUTs.
This article introduces a workflow that uses a virtual dyno to design and test a torque controller for an FEA-based high-fidelity PMSM machine. We’ll consider the following questions:
- What is a virtual dynamometer?
- Why use an FEA-based high-fidelity PMSM machine model?
- How to characterize the high-fidelity PMSM machine?
- How to design a torque controller using the characterization data?
The initial FEA data that we’ll be using for the high-fidelity PMSM machine model was generated from ANSYS® Maxwell® and JMAG®, and provided courtesy of ANSYS and JMAG.
What is a Virtual Dynamometer?
A virtual dynamometer is a model that brings the concept of the motor dynamometer to desktop simulation. Dynamometers are used to test torque or power of combustion engines or electric machines. Typically, the dyno can operate in all four quadrants on the torque-speed plane, enabling steady-state or transient motoring and generating tests of the coupled machine. Figure 1 shows a schematic of a dyno setup. The machine under test is an interior PMSM (IPM), while the dyno could be a PMSM, an induction machine, or any other machine capable of four-quadrant operation.
On the virtual dyno, a virtual speed or torque source replaces the dyno machine. The machine under test is driven to operate in torque mode by the speed source or in speed mode by the torque source, just as it would be on an actual dyno. In this way, all machine characterization and testing can be performed through simulation.
Why Use an FEA-Based PMSM Model?
Traditionally, the FEA-based motor design workflow and the motor control development workflow have proceeded separately because motor control engineers do not use FEA data for closed-loop control system simulation. Today, however, FEA simulation data can be imported into Simulink and Simscape Electrical™ for high-fidelity PMSM modeling. The high-fidelity PMSM model contains nonlinear characteristics due to saturation, as well as rotor-position-dependent spatial harmonic components in the back EMF, flux linkage, and torque.
Unlike a conventional linear lumped-parameter PMSM model, the FEA-based PMSM model behaves like an actual motor. This is because instead of having constant parameters for inductances and permanent magnet flux linkage, it has a nonlinear mapping between rotor position, flux linkage, current, and torque.
The FEA-based PMSM model enables control engineers to build a realistic closed-loop simulation and obtain the nonlinear operating characteristics of the machine even before it is manufactured, aligning control engineers with the motor design engineers during the early stages of development. In addition, the model gives motor control engineers the freedom to explore extreme operating conditions without out-of-bounds worries, since all tests are done using simulation in Simulink. The simulation results can guide actual dyno testing once the machine is manufactured. The Design of Experiments (DoE) setup requires an understanding of the machine’s characteristics, and the simulation helps engineers determine the minimum number of points to test.
How to Characterize the FEA-Based PMSM Model?
The purpose of characterizing the FEA-based PMSM model is to obtain the nonlinear flux linkage information under different operation points. In our case, the operation points are specified by steady-state currents on the synchronous reference frame—that is, by steady-state id and iq operation points.
With the virtual dyno, the speed of the PMSM model can be kept constant, and always below base speed (the speed at which the terminal voltage of the machine reaches its rated modulation index). In the example shown in Figure 2, under 500 V dc bus voltage the base speed is around 1800 rpm.
During the DoE setup, current id and iq commands are executed by a current controller (Figure 2). In the plant model, a speed source acting as the virtual dyno controls the speed of the PMSM model.
For every [id, iq] combination that is commanded, we run the simulation, allow the current response to reach steady state, and then log the following dataset: [id, iq, flux_d, flux_q, torque]. Because there are harmonics and ripples in the FEA-based PMSM machine, it is a good idea to take the average value of a certain duration under steady state before logging the dataset.
For example, in order to characterize the PMSM machine in the motoring region, all [id, iq] combinations specified in Figure 3 are swept. The red curve in Figure 3 indicates the current operation limit, or current-limit circle, for this particular PMSM machine. Although the machine itself will never operate beyond the current-limit circle during normal operation, under the virtual dyno we can push beyond this limit and sweep all marked operation points shown in Figure 3 without worrying about thermal issues in the actual machine.
We could complete characterization by scripting in MATLAB®. Alternatively, we can use Model-Based Calibration Toolbox™ to set up the DoE, automate the sweeping process, and collect data.
How to Design a Torque Controller Using the Characterization Data?
Now that we have characterization data for the high-fidelity PMSM machine, we can begin designing the torque controller. This involves three steps:
- Find the optimal operation boundary.
- Choose lookup table points.
- Test the torque controller performance.
Finding the Optimal Operation Boundary
The optimal operation boundary is defined such that under a specific torque command and speed feedback, it encompasses the machine’s optimal operating points. For a linear lumped-parameter PMSM model, the optimal operation boundary can be calculated mathematically using the PMSM machine’s parameters. This calculation will not be accurate for the real machine, however, since the real machine’s parameters change according to the operation points.
There are two ways to calculate a more accurate optimal operation boundary for the high-fidelity PMSM machine model. It can be calculated using the characterized dataset [id, iq, flux_d, flux_q, torque] and MATLAB scripts, or it can be derived using Model-Based Calibration Toolbox. With Model-Based Calibration Toolbox we can design experiments, set up objectives, and log data that meets those objectives. For example, one section of the optimal operation boundary is known as the maximum torque per ampere (MTPA) curve. To calculate this curve, we can use Model-Based Calibration Toolbox to set up a DoE that lets us sweep the current operation points along a current circle and monitor the torque until the maximum torque point is reached. Similar approaches can be used for calculating the maximum current and maximum torque per volt (MTPV) boundaries.
Figure 4 shows the calculated optimal operation boundary. We also plot contours of torque and speed because they serve as either objectives or constraints in the calculation process. We use Curve Fitting Toolbox™ to smooth out the optimal operation boundary and remove outliers resulting from either the nonlinearity of the machine or harmonics in the sweeping data.
Choosing Lookup Table Points
The second step for the torque controller design is to locate each operation point inside the optimal operation boundary according to each torque command and speed feedback. The goal is to locate operation points that not only meet different torque commands and voltage constraints but also minimize the stator winding copper losses. In Model-Based Calibration Toolbox we can set maximum torque per ampere (MTPA) as the objective, set the maximum phase current Is_max and voltage Vs_max as constraints, and then run the optimization.
Figure 5 shows a cluster of optimized operation points that meet these objectives and constraints. These optimized operation points will serve as the lookup table data points in the proposed torque controller shown in Figure 6.
Testing the Torque Controller Performance
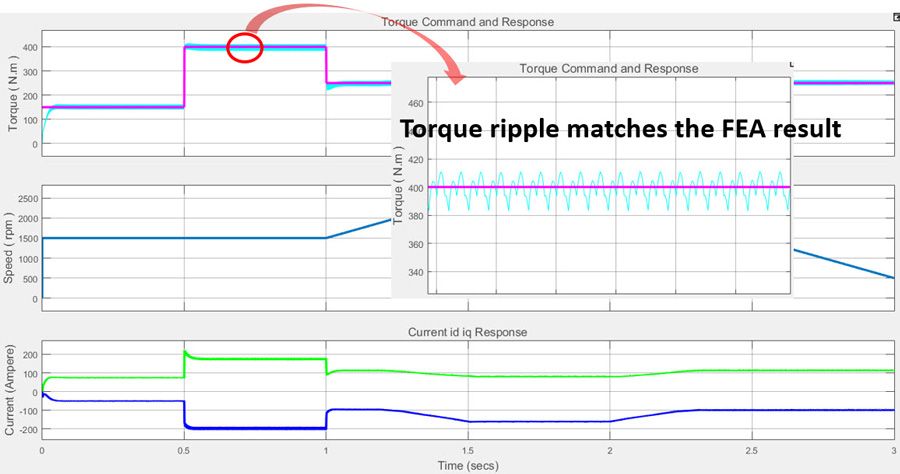
To test the controller, we run simulations with our virtual dyno. During the test, we initially keep the speed of the machine at 1500 rpm, which is below the base speed of around 1800 rpm. After 1 second, we increase the speed to the point where the machine enters the flux-weakening region. We give independent torque step commands, which are executed by the open-loop torque controller. Figure 7a shows the simulation results.
We can see from the performance waveform in Figure 7a that the torque is controlled to follow the torque step commands very well both below and above base speed.
Figure 7b gives a zoomed-in view of the torque ripple waveform that resulted from utilizing the high-fidelity PMSM model as the plant. (Note that the torque ripple is usually dampened by the mechanical system connecting to the PMSM, and does not pose any concern.)
We’re satisfied by these simulation results. The optimized torque control lookup tables, which are the final results of the proposed workflow, can now be tested on an actual dyno once the machine is manufactured.
By adopting this model-based virtual dynamometer approach, we can start the motor control development work almost concurrently with motor design, and provide useful insights for DoE and initial control lookup tables. The closed-loop simulation platform in this article can also be used to quickly verify motor drives performance without running an actual dyno.
Published 2017 - 93100V00