Simulink Design Optimization には、モデルパラメーターを解析および調整するための関数、対話型ツール、ブロックが用意されています。モデルの感度を決定して、モデルをテストデータに当てはめ、要件を満たすように調整できます。モンテカルロ シミュレーションや実験計画法などの手法を使用して、設計空間を調査し、モデルの動作に対するパラメーターの影響を計算できます。
Simulink Design Optimization は、モデルの精度を高めるのに役立ちます。テストデータを前処理して、摩擦係数や空力係数などのモデルパラメーターを自動的に推定し、推定結果を検証できます。
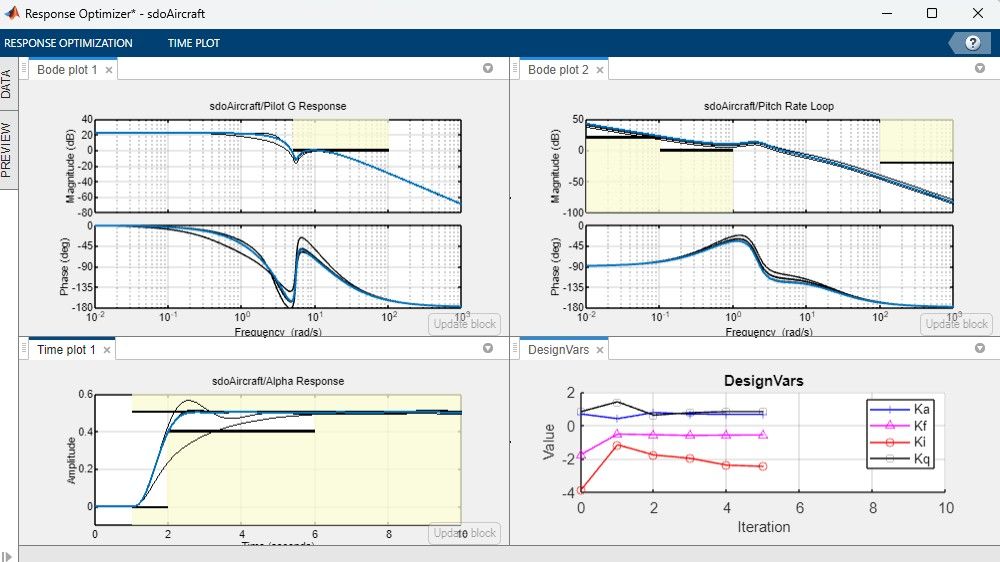
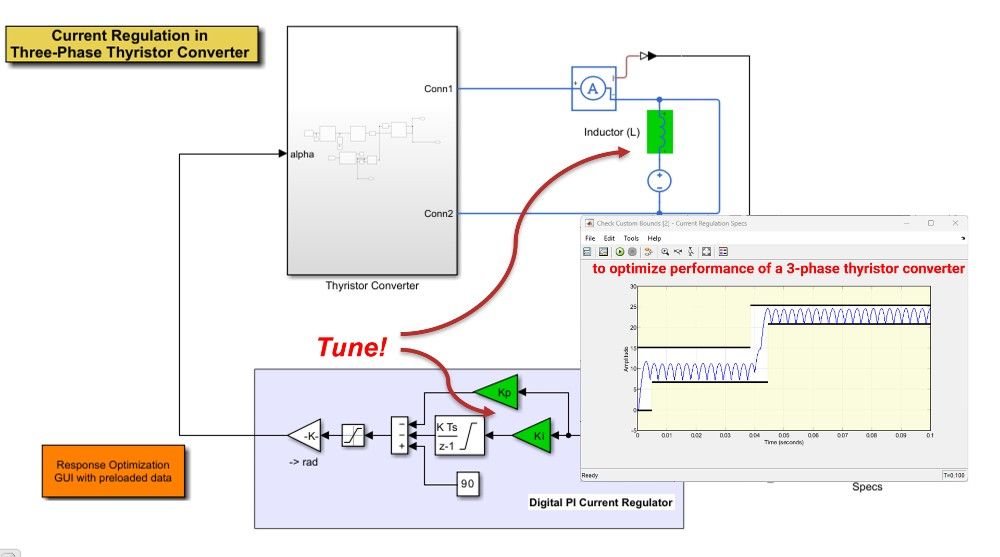
応答時間、帯域幅、エネルギー消費などのシステム設計の特性を改善するために、物理プラントのパラメーターと、アルゴリズムまたはコントローラーゲインを合わせて最適化できます。これらのパラメーターは、オーバーシュートや位相余裕などの時間領域と周波数領域の要件のほか、カスタム要件を満たすように調整できます。
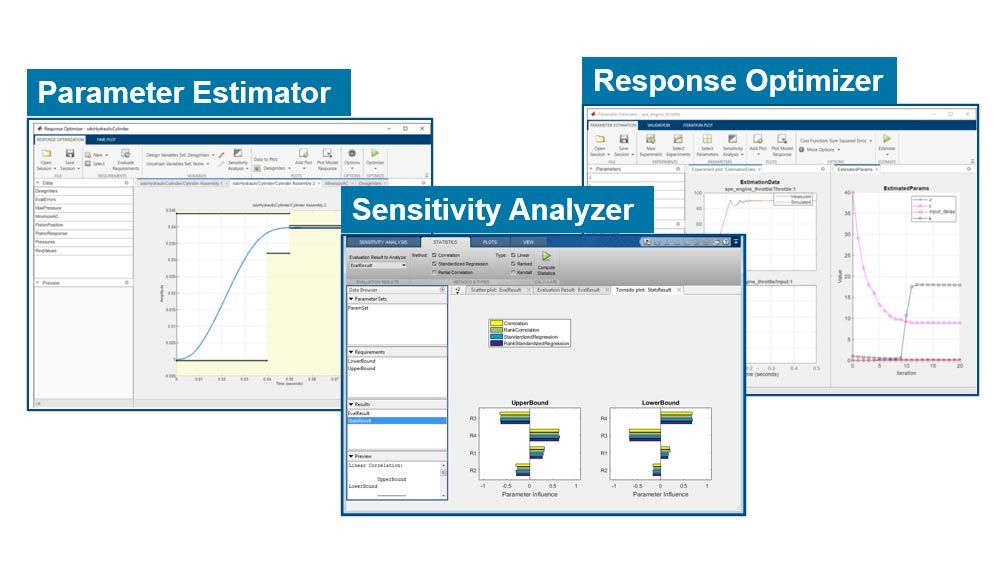
設計最適化アプリ
Simulink では、組み込みアプリを使用して、設計要件、決定変数、および最適化オプションの指定など、設計最適化問題を対話的に設定および求解します。アプリ内から MATLAB コードを生成して、展開や追加のカスタマイズを行います。
ドキュメンテーション | 例
パラメーター推定
パラメーター推定器アプリまたはコマンドライン関数を対話的に使用して、テストデータから Simulink モデルのパラメーターと状態を自動的に推定し、正確なプラントモデルを構築します。
ドキュメンテーション | 例
感度解析
感度アナライザーアプリを使用して、モデルの動作に最も大きな影響を与えるパラメーターを特定します。パラメーター推定と設計最適化について、より適切な初期条件を選択します。モンテカルロ シミュレーションを使用してモデルの設計空間を解析し、設計のロバスト性を確認します。
ドキュメンテーション | 例
プラントおよびコントローラーのパラメーターの協調最適化
物理プラントのパラメーターと、アルゴリズムまたはコントローラーゲインを合わせて最適化することにより、応答時間、帯域幅、エネルギー消費などのシステム設計の特性を改善します。
デジタルツインの調整
デプロイされたデジタルツインモデルのパラメーターを自動更新して、現在のアセットの状態に一致させます。Simulink Compiler を使用して、パラメーター推定ワークフローをデプロイします。
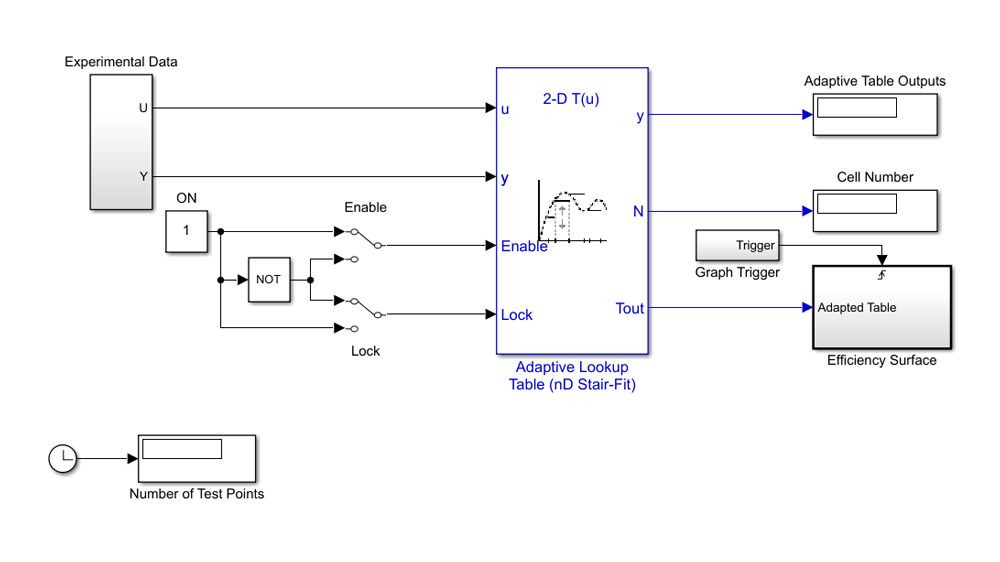
ルックアップテーブルの調整
バッテリー特性やゲインスケジュール コントローラーなどのアプリケーションに対してルックアップテーブルを調整します。ルックアップテーブルの値に、単調性や円滑性などの制約を課します。キャリブレーションの問題を解くには、適応ルックアップテーブルを使用します。
ドキュメンテーション | 例
設計最適化の高速化
Parallel Computing Toolbox を使用して、1 つのモデルで複数のシミュレーションを並列実行し、パラメーター推定、応答最適化、および感度解析を高速化します。Simulink の高速リスタート機能やアクセラレータ シミュレーション モードを使用して、設計最適化タスクを高速化します。
ドキュメンテーション | 例
最適化ソルバー
Optimization Toolbox や Global Optimization Toolbox からサロゲート、fmincon、パターン探索などの使用可能なソルバーを選択して、混合整数最適化、導関数に基づく、または導関数を使用しない最適化、などの様々な最適化問題を求解します。