このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

idwt2

単一レベル 2 次元逆離散ウェーブレット変換

構文

x = idwt2(cA,cH,cV,cD,wname)

x = idwt2(cA,cH,cV,cD,LoR,HiR)

x = idwt2(___,s)

x = idwt2(___,'mode',mode)

x = idwt2(cA,[],[],[],___)

x = idwt2([],cH,[],[],___)

x = idwt2([],[],cV,[],___)

x = idwt2([],[],[],cD,___)

説明

x = idwt2(cA,cH,cV,cD,wname) は、wname で指定されたウェーブレットを使用し、Approximation 行列 cA と Detail 行列 cH (水平方向)、cV (垂直方向)、および cD (対角方向) に基づいて、単一レベル 2 次元ウェーブレット再構成を実行します。詳細については、dwt2 を参照してください。

sa = size(cA) = size(cH) = size(cV) = size(cD) とし、lf を wname に関連付けられた再構成フィルターの長さに等しくします。DWT 拡張モードが周期化に設定されている場合、x のサイズ sx は 2*sa と等しくなります。他の拡張モードの場合、sx = 2*sa-lf+2 となります。詳細については、dwtmode を参照してください。

x = idwt2(cA,cH,cV,cD,LoR,HiR) は、指定されたローパス ウェーブレット再構成フィルター LoR とハイパス ウェーブレット再構成フィルター HiR をそれぞれ使用します。

x = idwt2(___,s) は、前述の構文のいずれかを使用して、再構成のサイズ s の中央部を返します。

x = idwt2(___,'mode',mode) は、指定された拡張モード mode を使用して、ウェーブレット再構成を計算します。詳細については、dwtmode を参照してください。この構文は、前述のいずれの構文でも使用できます。

x = idwt2(cA,[],[],[],___) は、Approximation 係数の行列 cA に基づいて、単一レベルの再構成された Approximation 係数の行列 x を返します。

x = idwt2([],cH,[],[],___) は、水平方向の Detail 係数の行列 cH に基づいて、単一レベルの再構成された Approximation 係数の行列 x を返します。

x = idwt2([],[],cV,[],___) は、垂直方向の Detail 係数の行列 cV に基づいて、単一レベルの再構成された Approximation 係数の行列 x を返します。

x = idwt2([],[],[],cD,___) は、対角方向の Detail 係数の行列 cD に基づいて、単一レベルの再構成された Approximation 係数の行列 x を返します。

例

単一レベル 2 次元ウェーブレット再構成

イメージを読み込みます。

load woman
whos X

  Name        Size              Bytes  Class     Attributes

  X         256x256            524288  double              

ワークスペース変数 X にはイメージが格納されます。db4 ウェーブレットを使用して、X の単一レベル ウェーブレット分解を実行します。

[cA1,cH1,cV1,cD1] = dwt2(X,'db4');

レベル 1 の係数を使用して X の分解を反転します。

A0 = idwt2(cA1,cH1,cV1,cD1,'db4');

完全再構成されているかチェックします。

max(abs(X(:)-A0(:)))

ans = 3.4171e-10

Detail 係数のウェーブレット再構成

イメージを読み込みます。

load tartan
imagesc(X)
colormap(gray)

db4 ウェーブレットを使用して、単一レベル ウェーブレット分解を実行します。

[cA,cH,cV,cD] = dwt2(X,'db4');

対角方向の Detail 係数のみを使用して、ウェーブレット再構成を求めます。

xrecD = idwt2([],[],[],cD,'db4');

今度は水平方向と対角方向の Detail 係数を使用して、2 番目のウェーブレット再構成を求めます。

xrecHD = idwt2([],cH,[],cD,'db4');

両方の再構成を表示します。

subplot(1,2,1)
imagesc(xrecD)
title('Diagonal')
subplot(1,2,2)
imagesc(xrecHD)
title('Horizontal-Diagonal')
colormap(gray)

入力引数

cA — Approximation 係数

配列

Approximation 係数。配列として指定します。cA は dwt2 の出力にする必要があります。

データ型: double

cH — 水平方向の Detail 係数

配列

水平方向の Detail 係数。配列として指定します。cD は dwt2 の出力にする必要があります。

データ型: double

cV — 垂直方向の Detail 係数

配列

垂直方向の Detail 係数。配列として指定します。cV は dwt2 の出力にする必要があります。

データ型: double

cD — 対角方向の Detail 係数

配列

対角方向の Detail 係数。配列として指定します。cD は dwt2 の出力にする必要があります。

データ型: double

wname — ウェーブレット

文字ベクトル | string スカラー

ウェーブレット。文字ベクトルまたは string スカラーとして指定します。idwt2 は、直交ウェーブレットまたは双直交ウェーブレットのみをサポートします。直交ウェーブレットと双直交ウェーブレットの一覧については、wfilters を参照してください。

指定するウェーブレットは、Approximation 係数と Detail 係数を求めるために使用するウェーブレットと同じでなければなりません。

LoR,HiR — ウェーブレット再構成フィルター

偶数長の実数値のベクトル

ウェーブレット再構成フィルター。偶数長の実数値ベクトルのペアとして指定します。LoR はローパス再構成フィルター、HiR はハイパス再構成フィルターです。LoR と HiR の長さは等しくなければなりません。詳細については、wfilters を参照してください。

データ型: double

s — 中央部のサイズ

2 要素ベクトル

返す再構成の中央部のサイズ。正の整数の 2 要素ベクトルとして指定します。s は、x のサイズである sx 未満でなければなりません。

データ型: double

mode — DWT 拡張モード

文字ベクトル | string スカラー

ウェーブレット再構成で使用する DWT 拡張モード。文字ベクトルまたは string スカラーとして指定します。拡張モードの選択肢については、dwtmode を参照してください。

ヒント

• cA、cH、cV、および cD がインデックス付きイメージ解析から取得される場合、それらは M 行 N 列の行列になります。cA、cH、cV、および cD がトゥルーカラー イメージの解析から取得される場合、それらは M×N×3 の配列になります。

  イメージ形式の詳細については、image と imfinfo を参照してください。

アルゴリズム

イメージの 2 次元ウェーブレット再構成のアルゴリズムは 1 次元の場合と同様です。2 次元のウェーブレット関数とスケーリング関数は、1 次元のウェーブレット関数とスケーリング関数のテンソル積を取ることで得られます。このような 2 次元逆 DWT は、4 つの成分 (レベル j+1 の Approximation と 3 つの方向 (水平方向、垂直方向、および対角方向) の Detail) から取得したレベル j の Approximation 係数の再構成になります。次のチャートに、イメージの基本的な再構成ステップを示します。

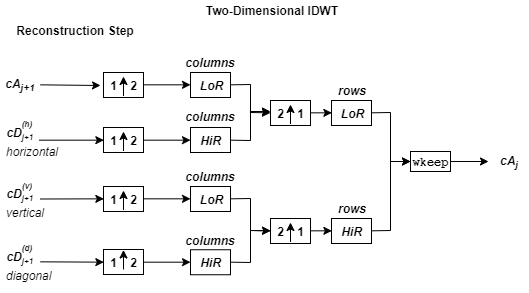
ここで

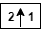• — 列をアップサンプリング: 奇数インデックスの列にゼロを挿入

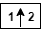• — 行をアップサンプリング: 奇数インデックスの行にゼロを挿入

• — フィルター X でエントリの行を畳み込み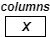

• — フィルター X でエントリの列を畳み込み

参照

[1] Daubechies, Ingrid. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics 61. Philadelphia, Pa: Society for Industrial and Applied Mathematics, 1992.

[2] Mallat, S.G. “A Theory for Multiresolution Signal Decomposition: The Wavelet Representation.” IEEE Transactions on Pattern Analysis and Machine Intelligence 11, no. 7 (July 1989): 674–93. https://doi.org/10.1109/34.192463.

[3] Meyer, Y. Wavelets and Operators. Translated by D. H. Salinger. Cambridge, UK: Cambridge University Press, 1995.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• 入力 wname は定数でなければなりません。

GPU コード生成

GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

使用上の注意および制限:

• 入力 wname は定数でなければなりません。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

使用上の注意および制限:

• 'sym' および 'per' 拡張モードのみサポートしています。dwtmode を参照してください。

バージョン履歴

R2006a より前に導入

参考

dwt2 | dwtmode | upwlev2