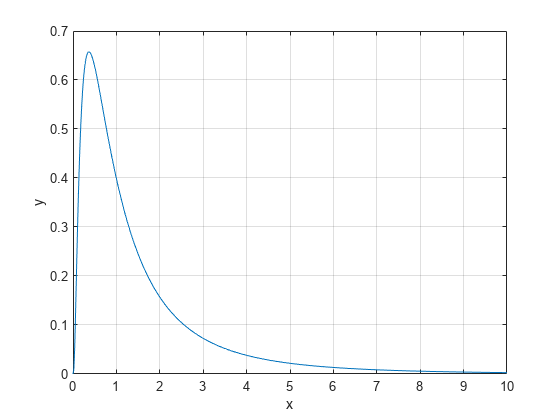
lognpdf
対数正規の確率密度関数
説明
例
入力引数
出力引数
詳細
代替機能
lognpdfは対数正規分布専用の関数です。Statistics and Machine Learning Toolbox™ には、さまざまな確率分布をサポートする汎用関数pdfもあります。pdfを使用するには、LognormalDistribution確率分布オブジェクトを作成し入力引数として渡すか、確率分布名とそのパラメーターを指定します。分布専用の関数lognpdfは汎用関数pdfより高速です。確率分布の累積分布関数 (cdf) または確率密度関数 (pdf) のプロットを対話的に作成するには、確率分布関数アプリを使用します。
参照
[1] Mood, A. M., F. A. Graybill, and D. C. Boes. Introduction to the Theory of Statistics. 3rd ed., New York: McGraw-Hill, 1974. pp. 540–541.
[2] Evans, M., N. Hastings, and B. Peacock. Statistical Distributions. 2nd ed., Hoboken, NJ: John Wiley & Sons, Inc., 1993.
拡張機能
バージョン履歴
R2006a より前に導入