カーネル分布オブジェクトのデータへの当てはめ
この例では、カーネル確率分布オブジェクトを標本データに当てはめる方法を示します。
手順 1. 標本データを読み込む。
標本データを読み込みます。
load carsmall;このデータには、さまざまな車種およびモデルのガロンあたりの走行マイル数 (MPG) の測定値が格納され、生産国 (Origin)、モデル年 (Year)、その他の車両の特性によってグループ化されています。
手順 2. カーネル分布オブジェクトを当てはめる。
fitdist を使用し、カーネル確率分布オブジェクトをすべての車種のガロンあたりの走行マイル数 (MPG) データに当てはめます。
pd = fitdist(MPG,'Kernel')pd =
KernelDistribution
Kernel = normal
Bandwidth = 4.11428
Support = unbounded
これにより prob.KernelDistribution オブジェクトが作成されます。既定では、特に指定しない限り、fitdist は通常のカーネル平滑化関数を使用し、正規分布の密度を推定するのに最適な帯域幅を選択します。近似に関する情報にアクセスし、関連するオブジェクト関数を使用してさらに計算を実行できます。
手順 3. 記述統計を計算する。
近似したカーネル分布の平均、中央値および標準偏差を計算します。
m = mean(pd)
m = 23.7181
med = median(pd)
med = 23.4841
s = std(pd)
s = 8.9896
手順 4. pdf を計算してプロットする。
近似したカーネル分布の pdf を計算してプロットします。
figure x = 0:1:60; y = pdf(pd,x); plot(x,y,'LineWidth',2) title('Miles per Gallon') xlabel('MPG')
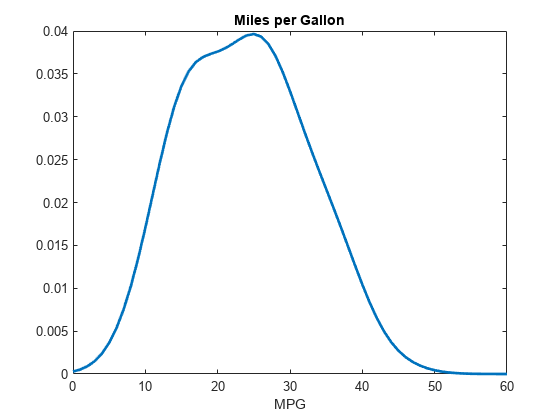
プロットは、全車種の MPG データに当てはめたカーネル分布の pdf を示しています。分布は右裾が大きく広がっているため、若干偏っていますが、滑らかでほぼ対称的です。
手順 5. 乱数を生成する。
近似したカーネル分布から乱数のベクトルを生成します。
rng('default') % For reproducibility r = random(pd,1000,1); figure hist(r); set(get(gca,'Children'),'FaceColor',[.8 .8 1]); hold on y = y*5000; % Scale pdf to overlay on histogram plot(x,y,'LineWidth',2) title('Random Numbers Generated From Distribution') hold off
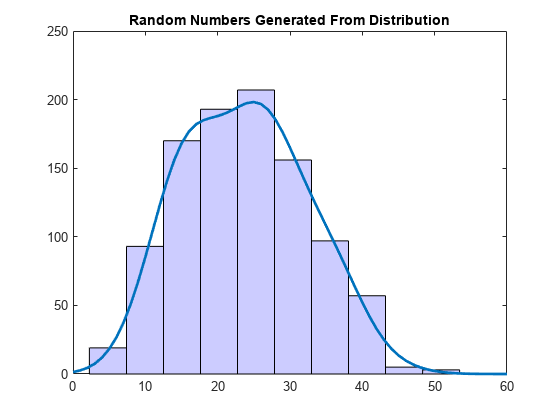
標本データに当てはめたノンパラメトリックなカーネル分布から乱数が生成されるため、ヒストグラムは pdf プロットと同様の形状をしています。
参考
fitdist | ksdensity | KernelDistribution
