anova1
1 因子 ANOVA
構文
説明
p = anova1(y)y について 1 因子 ANOVA を実行し、p 値を返します。anova1 は y の各列を個別のグループとして扱います。関数は、平均が同じ複数の母集団から y の列の標本が抽出されたという仮説を、母集団の平均はすべて同じではないという対立仮説に対して検定します。関数は、y の各グループについての箱ひげ図と、標準的な ANOVA 表 (tbl) も表示します。
p = anova1(y,group,displayopt)displayopt が 'on' (既定値) の場合は表示され、displayopt が 'off' の場合は非表示になります。
例
1 因子 ANOVA
定数の列が含まれている標本データ行列 y を作成し、平均が 0 で標準偏差が 1 の無作為な正規分布の外乱を加えます。
y = meshgrid(1:5); rng default; % For reproducibility y = y + normrnd(0,1,5,5)
y = 5×5
1.5377 0.6923 1.6501 3.7950 5.6715
2.8339 1.5664 6.0349 3.8759 3.7925
-1.2588 2.3426 3.7254 5.4897 5.7172
1.8622 5.5784 2.9369 5.4090 6.6302
1.3188 4.7694 3.7147 5.4172 5.4889
1 因子 ANOVA を実行します。
p = anova1(y)
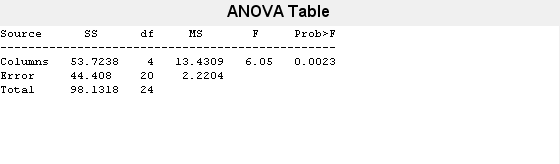
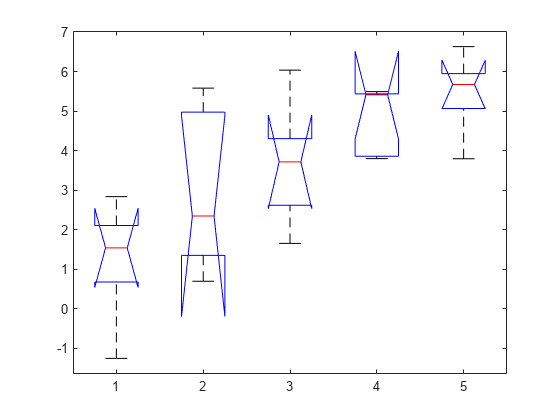
p = 0.0023
ANOVA 表には、グループ間の変動 (Columns) とグループ内の変動 (Error) が示されています。SS は二乗和、df は自由度です。全体の自由度は、観測値の総数から 1 を減算した 25 - 1 = 24 です。グループ間の自由度は、グループ数から 1 を減算した 5 - 1 = 4 です。グループ内の自由度は、全体の自由度からグループ間の自由度を減算した 24 - 4 = 20 です。
MS は平均二乗誤差で、変動の原因ごとの SS/df です。F 統計量は、平均二乗誤差の比率です (13.4309/2.2204)。p 値は、この統計量の値が検定統計量の計算値より大きくなる確率 P(F > 6.05) です。p 値は 0.0023 という小さい値なので、列の平均には有意な違いがあることがわかります。
1 因子 ANOVA を使用したビームの強度の比較
標本データを入力します。
strength = [82 86 79 83 84 85 86 87 74 82 ... 78 75 76 77 79 79 77 78 82 79]; alloy = {'st','st','st','st','st','st','st','st',... 'al1','al1','al1','al1','al1','al1',... 'al2','al2','al2','al2','al2','al2'};
このデータは、Hogg の構造化ビームの強度の研究 (1987 年) からのデータです。ベクトル strength は、3,000 ポンドの力が加わったとき、1,000 分の 1 インチごとにビームのたわみを測定します。ベクトル alloy では、各ビームを鋼鉄 ('st')、合金 1 ('al1') または合金 2 ('al2') として識別します。この例では alloy が並べ替えられていますが、グループ化変数を並べ替える必要はありません。
「鋼鉄のビームの強度は、2 つ以上の高価な合金で製造されたビームの強度と等しくなる」という帰無仮説を検定します。図の表示を無効にし、ANOVA の結果を cell 配列に取得します。
[p,tbl] = anova1(strength,alloy,'off')p = 1.5264e-04
tbl=4×6 cell array
{'Source'} {'SS' } {'df'} {'MS' } {'F' } {'Prob>F' }
{'Groups'} {[184.8000]} {[ 2]} {[ 92.4000]} {[ 15.4000]} {[1.5264e-04]}
{'Error' } {[102.0000]} {[17]} {[ 6.0000]} {0x0 double} {0x0 double }
{'Total' } {[286.8000]} {[19]} {0x0 double} {0x0 double} {0x0 double }
全体の自由度は、観測値の総数から 1 を減算した です。グループ間の自由度は、グループ数から 1 を減算した です。グループ内の自由度は、全体の自由度からグループ間の自由度を減算した です。
MS は平均二乗誤差で、変動の原因ごとの SS/df です。F 統計量は、平均二乗誤差の比率です。p 値は、この統計量が検定統計量より大きい値になる確率です。p 値は 1.5264e-04 なので、帰無仮説は棄却されます。
cell 配列のインデックスを指定すると、ANOVA 表の値を取得できます。F 統計量の値と p 値を新しい変数 Fstat および pvalue に格納します。
Fstat = tbl{2,5}Fstat = 15.4000
pvalue = tbl{2,6}pvalue = 1.5264e-04
1 因子 ANOVA の多重比較
標本データを入力します。
strength = [82 86 79 83 84 85 86 87 74 82 ... 78 75 76 77 79 79 77 78 82 79]; alloy = {'st','st','st','st','st','st','st','st',... 'al1','al1','al1','al1','al1','al1',... 'al2','al2','al2','al2','al2','al2'};
このデータは、Hogg の構造化ビームの強度の研究 (1987 年) からのデータです。ベクトル strength は、3,000 ポンドの力が加わったとき、1,000 分の 1 インチごとにビームのたわみを測定します。ベクトル alloy では、各ビームを鋼鉄 (st)、合金 1 (al1) または合金 2 (al2) として識別します。この例では alloy が並べ替えられていますが、グループ化変数を並べ替える必要はありません。
anova1 を使用して 1 因子 ANOVA を実行します。構造体 stats が返されます。この構造体には、multcompareで多重比較を実行するために必要な統計量が含まれています。
[~,~,stats] = anova1(strength,alloy);

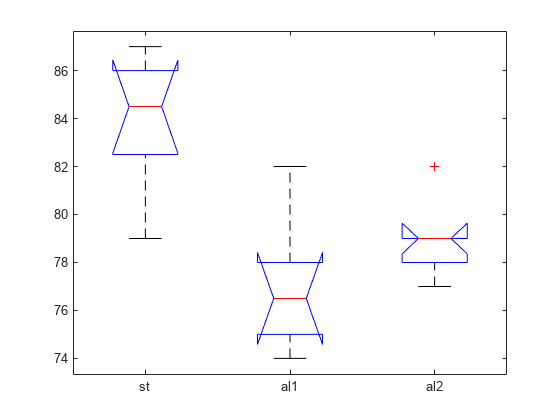
p 値は 0.0002 という小さい値なので、ビームの強度が同じではないことがわかります。
ビームの平均強度について多重比較を実行します。
[c,~,~,gnames] = multcompare(stats);
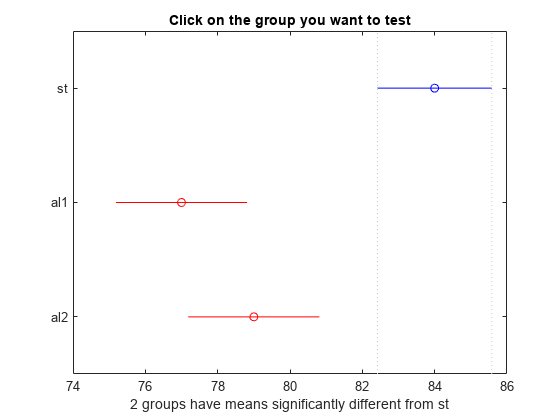
図の青いバーは、鋼鉄の平均材料強度の比較区間を表しています。赤いバーは、合金 1 および合金 2 の平均材料強度の比較区間を表しています。どちらの赤いバーも青いバーと重なっていないので、鋼鉄と合金 1 および合金 2 では平均材料強度が有意に異なることがわかります。有意差は合金 1 および 2 を表すバーをクリックすると確認できます。
多重比較の結果と該当するグループ名を table で表示します。
tbl = array2table(c,"VariableNames", ... ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"]); tbl.("Group A") = gnames(tbl.("Group A")); tbl.("Group B") = gnames(tbl.("Group B"))
tbl=3×6 table
Group A Group B Lower Limit A-B Upper Limit P-value
_______ _______ ___________ ___ ___________ __________
{'st' } {'al1'} 3.6064 7 10.394 0.00016831
{'st' } {'al2'} 1.6064 5 8.3936 0.0040464
{'al1'} {'al2'} -5.628 -2 1.628 0.35601
初めの 2 列には、比較したグループのペアが示されています。4 列目には、推定したグループ平均の間の差が示されています。3 列目と 5 列目には、真の平均の差に関する 95% 信頼区間の下限と上限が示されています。6 列目には、対応するグループ間では真の平均の差がゼロに等しいという仮説の p 値が示されています。
最初の 2 行は、最初のグループ (鋼鉄) を含むいずれの比較も、0 を含まない信頼区間をもつことを示します。対応する p 値 (それぞれ 1.6831e-04 と 0.0040) が小さいので、これらの差は有意です。
3 行目には、2 つの合金の強度に有意差がないことが示されています。差の 95% 信頼区間は [-5.6,1.6] なので、真の差がゼロであるという仮説を棄却できません。6 列目の対応する p 値は 0.3560 なので、この結果を確定できます。
入力引数
y — 標本データ
ベクトル | 行列
標本データ。ベクトルまたは行列として指定します。
yがベクトルである場合、入力引数groupを指定しなければなりません。groupの各要素は、y内の対応する要素のグループ名を表します。関数anova1は、 対応するgroup名が同じであればy値を同じグループの一部として扱います。この設計は、各グループに含まれている要素の数が異なる場合 (不平衡な ANOVA) に使用します。
yが行列で、groupを指定しない場合、anova1はyの各列を個別のグループとして扱います。この形式では、各列の母集団平均が等しいかどうかが評価されます。各グループの要素数が同じ場合 (平衡型 ANOVA)、この形式を使用します。
yが行列で、groupを指定する場合、groupの各要素は、yの対応する列のグループ名を表します。関数anova1は、同じグループ名をもつ列を同じグループの一部として扱います。
メモ
anova1 は、y 内の任意の NaN 値を無視します。また、group に空または NaN の値が含まれている場合、anova1 は y 内の対応する観測値を無視します。関数 anova1 は、空または NaN の値を無視した後、各グループに同じ数の観測値がある場合、平衡型 ANOVA を実行します。そうでない場合、anova1 は不平衡な ANOVA を実行します。
データ型: single | double
group — グループ化変数
数値ベクトル | logical ベクトル | categorical ベクトル | 文字配列 | string 配列 | 文字ベクトルの cell 配列
グループ名を含むグループ化変数。数値ベクトル、logical ベクトル、categorical ベクトル、文字配列、string 配列、または文字ベクトルの cell 配列として指定します。
yがベクトルの場合、groupの各要素は、y内の対応する要素のグループ名を表します。関数anova1は、 対応するgroup名が同じであればy値を同じグループの一部として扱います。
N は、観測の合計数です。
yが行列の場合、groupの各要素は、yの対応する列のグループ名を表します。関数anova1は、同じグループ名をもつyの列を同じグループの一部として扱います。
行列の標本データ
yについてグループ名を指定しない場合は、空の配列 ([]) を入力するか、この引数を省略します。この場合、anova1はyの各列を個別のグループとして扱います。
group に空または NaN の値が含まれている場合、anova1 は y 内の対応する観測値を無視します。
グループ化変数の詳細は、グループ化変数を参照してください。
例: y がグループ 1、2、および 3 に分類される観測値をもつベクトルの場合 'group',[1,2,1,3,1,...,3,1]
例: y が、グループ赤、白、および黒に分類される 5 つの列をもつ行列の場合 'group',{'white','red','white','black','red'}
データ型: single | double | logical | categorical | char | string | cell
displayopt — ANOVA 表と箱ひげ図を表示するためのインジケーター
'on' (既定値) | 'off'
ANOVA 表と箱ひげ図を表示するためのインジケーター。'on' または 'off' として指定します。displayopt が 'off' の場合、anova1 は出力引数のみを返します。標準的な ANOVA 表と箱ひげ図は表示しません。
例: p = anova(x,group,'off')
出力引数
p — F 検定の p 値
スカラー値
F 検定の p 値。スカラー値として返されます。p 値は、F 統計量が検定統計量の計算値より大きい値になる確率です。anova1 では、すべてのグループ平均が互いに等しいという帰無仮説を、少なくとも 1 つのグループ平均が他と異なるという対立仮説に対して検定します。この関数では、F 分布の累積分布関数から p 値を導き出します。
有意水準より小さい p 値は、少なくとも 1 つの標本平均が他と有意に異なることを示します。一般的な有意水準は 0.05 または 0.01 です。
tbl — ANOVA 表
cell 配列
ANOVA 表。cell 配列として返されます。tbl には 6 つの列があります。
| 列 | 定義 |
|---|---|
source | 変化の原因。 |
SS | 各原因による二乗和 |
df | 各原因に関連付けられている自由度N が観測値の総数、k がグループの数であるとします。すると、N - k はグループ内の自由度 (Error)、k - 1 はグループ間の自由度 (Columns)、N - 1 は全体の自由度 (N - 1 = (N - k) + (k - 1)) になります。 |
MS | 各原因の平均二乗 (比率 SS/df) |
F | F 統計量 (平均二乗の比率) |
Prob>F | p 値 (F 統計量が検定統計量の計算値より大きい値になる確率)。anova1 では F 分布の累積分布関数からこの確率が導き出されます。 |
ANOVA 表の各行には、データの変動性が原因別に示されます。
| 行 | 定義 |
|---|---|
Groups | グループの平均の違いによる変動性 (グループ "間" の変動性) |
Error | 各グループのデータ間の違いとグループの平均の違いによる変動性 (グループ "内" の変動性) |
Total | 全体の変動性 |
stats — 多重比較検定用の統計量
構造体
多重比較検定用の統計量。次の表に記載されているフィールドが含まれている構造体として返されます。
| フィールド名 | 定義 |
|---|---|
gnames | グループの名前 |
n | 各グループの観測値の数 |
source | stats の出力のソース |
means | 平均の推定値 |
df | (グループ内の) 誤差自由度 (N - k。ここで N は観測値の総数、k はグループ数) |
s | 平均二乗誤差の平方根 |
詳細
箱ひげ図
anova1 は、y 内の各グループの観測値の箱ひげ図を返します。箱ひげ図を使用すると、グループの位置パラメーターを視覚的に比較できます。
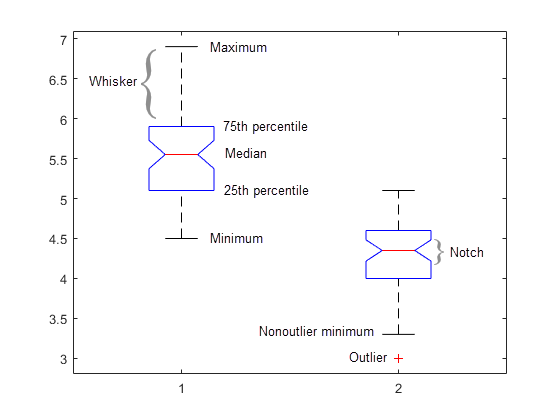
各ボックスで、中央のマークは中央値 (2 番目の分位数、q2)、ボックスの端は 25 番目と 75 番目の百分位数 (1 番目と 3 番目の分位数、それぞれ q1 および q3) を表します。ひげは、外れ値とは見なされない最も極端なデータ点まで延びます。外れ値は '+' 記号を使用して個別にプロットされます。ひげの端は q3 + 1.5 × (q3 – q1) および q1 – 1.5 × (q3 – q1) に対応します。
箱ひげ図には中央値の比較のためのノッチが含まれます。ノッチで表される区間がオーバーラップしない場合、2 つの中央値は 5% の水準で有意差があります。この検定は ANOVA で実行する F 検定とは異なりますが、ボックスの中央の線が大きく異なる場合は F 統計量の値が大きくなり、p 値が小さくなります。ノッチの端は q2 – 1.57(q3 – q1)/sqrt(n) と q2 + 1.57(q3 – q1)/sqrt(n) に対応します。ここで、n は NaN 値を除いた観測数です。場合によっては、ノッチがボックスの外まで伸びることもあります。
代替機能
anova1 を使用する代わりに、関数 anova を使用して anova オブジェクトを作成できます。関数 anova には次の利点があります。
関数
anovaでは、ANOVA モデルのタイプ、二乗和のタイプ、カテゴリカルとして扱う因子を指定できます。anovaでは、table の予測子と応答の入力引数もサポートされます。anovaオブジェクトのプロパティには、anova1で返される出力に加えて以下が含まれます。ANOVA モデルの式
当てはめられる ANOVA モデルの係数
残差
因子と応答データ
anovaオブジェクトを当てはめた後に、anovaのオブジェクト関数を使用して追加の解析を実行できます。たとえば、ANOVA の平均の多重比較についての対話型プロットを作成したり、因子の各値の平均応答推定を取得したり、分散成分推定を計算したりできます。
参照
[1] Hogg, R. V., and J. Ledolter. Engineering Statistics. New York: MacMillan, 1987.
バージョン履歴
R2006a より前に導入
MATLAB コマンド
次の MATLAB コマンドに対応するリンクがクリックされました。
コマンドを MATLAB コマンド ウィンドウに入力して実行してください。Web ブラウザーは MATLAB コマンドをサポートしていません。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)