このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
sgolay
Savitzky-Golay フィルター設計
説明
例
入力引数
出力引数
アルゴリズム
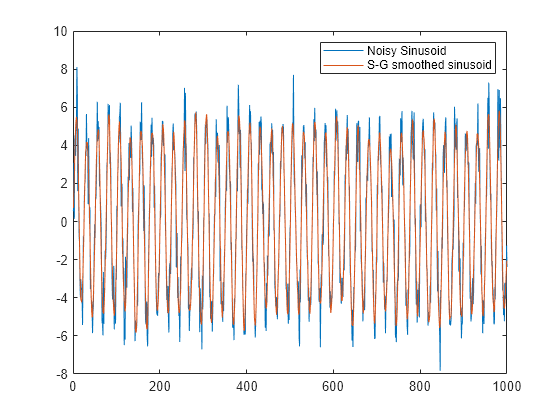
Savitzky-Golay フィルターは、周波数範囲が広いノイズ信号の平滑化に使用されます。Savitzky-Golay 平滑化フィルターは、標準の平均化 FIR フィルターに比べ、信号の高周波数成分を維持しやすいという傾向があります。ただし、ノイズ レベルが著しく高い場合のノイズの除去には優れていません。
一般に、フィルター処理では、信号の各点を、その点を中心とする移動ウィンドウに含まれる信号値のいくつかの組み合わせで置き換えます。この処理は、近傍点はほぼ同じ基礎値を測定するという仮定に基づいています。たとえば、移動平均フィルターは、各データ点を周囲のデータ点の局所的な平均で置き換えます。与えられたデータ点が左に k 点、右に k 点をもち、ウィンドウの長さの合計が L = 2k + 1 である場合、移動平均フィルターは次の置き換えを行います。
Savitzky-Golay フィルターは、ウィンドウ内の信号値で n 次多項式を最小二乗近似し、近似された多項式曲線について計算された中心点を新たに平滑化されたデータ点として取得することで、この理念を一般化します。与えられた点 xs について、次のようになります。
または、行列という観点では次のようになります。
Savitzky-Golay 推定値を求めるには、H の疑似逆数を使用して a を計算してから、H でプリマルチプライ処理を行います。
悪条件を回避するために、sgolay では、関数 qr を使用して、B = QQT という観点で H の無駄のないサイズの分解を H = QR として計算します。
B は 1 回のみ計算する必要があります。大半の信号点についての Savitzky-Golay 推定値は、B の中心の行で信号の畳み込みを行うことによって得られます。結果はフィルター処理された信号の定常状態部分です。B の最初の k 行からは最初の過渡状態が得られ、B の最後の k 行からは最後の過渡状態が得られます。例については、sgolayfilt を参照してください。ウィンドウの長さを増やすことでノイズをさらに抑制できますが、過渡状態付近でギブズ現象に類似したリンギングが発生します。
参照
[1] Orfanidis, Sophocles J. Introduction to Signal Processing. Englewood Cliffs, NJ: Prentice Hall, 1996.
[2] Press, William H., Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery. Numerical Recipes in C: The Art of Scientific Computing. New York: Cambridge University Press, 1992.
[3] Schafer, Ronald W. “What Is a Savitzky-Golay Filter? [Lecture Notes].” IEEE Signal Processing Magazine Vol. 28, Number 4, July 2011, pp. 111–117. https://doi.org/10.1109/MSP.2011.941097.
拡張機能
バージョン履歴
R2006a より前に導入
参考
fir1 | firls | filter | sgolayfilt