このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
goertzel
2 次 Goertzel アルゴリズムを使用した離散フーリエ変換
説明
例
入力引数
出力引数
アルゴリズム
Goertzel アルゴリズムは、次のインパルス応答をもつ N 点の入力 x(n), n = 0, 1, …, N – 1 の畳み込みとして離散フーリエ変換 X(k) を実装します。
ここで、単位ステップのシーケンス u(n) は、n ≥ 0 の場合は 1 であり、それ以外の場合は 0 となります。k は整数である必要はありません。周波数 f = kfs/N のとき (fs はサンプル レート)、変換は次の値をもちます。
ここで、
かつ x(N) = 0 です。インパルス応答の Z 変換は次のようになります。
これを使用して直接型 II を次のように実装します。
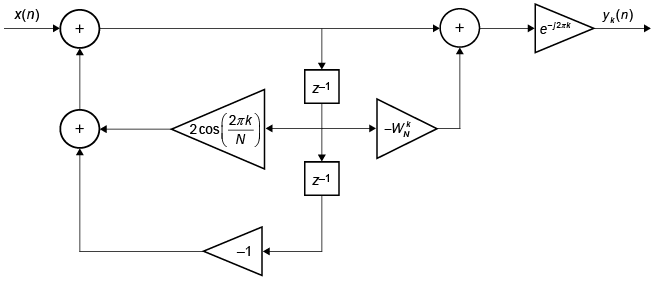
goertzel の出力と Goertzel アルゴリズムの直接実装による結果を比較します。入力信号には、50 Hz で 10 秒間サンプリングされ、ホワイト ガウス ノイズに組み込まれたチャープを使用します。測定中、チャープの周波数は 15 Hz から 20 Hz に線形で増加します。fs/N の整数倍ではない周波数で離散フーリエ変換を計算します。goertzel を呼び出す場合、MATLAB® のベクトルは 0 から N – 1 ではなく 1 から N で実行されることに注意してください。高精度の結果が得られます。
fs = 50; t = 0:1/fs:10-1/fs; N = length(t); xn = chirp(t,15,t(end),20)+randn(1,N)/100; f0 = 17.36; k = N*f0/fs; ykn = filter([1 -exp(-2j*pi*k/N)],[1 -2*cos(2*pi*k/N) 1],[xn 0]); Xk = exp(-2j*pi*k)*ykn(end); dft = goertzel(xn,k+1); df = abs(Xk-dft)
df = 4.3634e-12
代替方法
次の方法で DFT を計算することもできます。
参照
[1] Burrus, C. Sidney, and Thomas W. Parks. DFT/FFT and Convolution Algorithms: Theory and Implementation. New York: John Wiley & Sons, 1985.
[2] Proakis, John G., and Dimitris G. Manolakis. Digital Signal Processing: Principles, Algorithms, and Applications. 3rd Edition. Upper Saddle River, NJ: Prentice Hall, 1996.
[3] Sysel, Petr, and Pavel Rajmic. “Goertzel Algorithm Generalized to Non-Integer Multiples of Fundamental Frequency.” EURASIP Journal on Advances in Signal Processing. Vol. 2012, Number 1, December 2012, pp. 56-1–56-8. https://doi.org/10.1186/1687-6180-2012-56.
拡張機能
バージョン履歴
R2006a より前に導入