このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
dpss
離散扁長回転楕円体 (スレピアン) 列
構文
説明
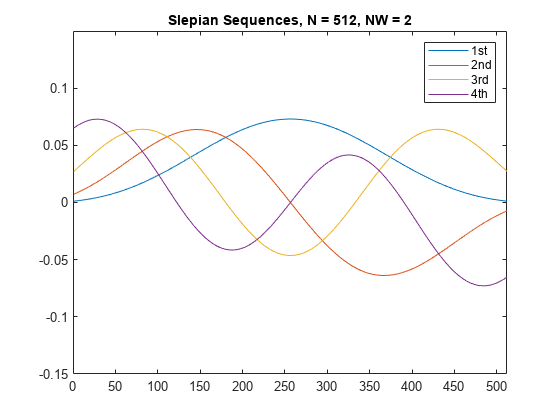
dps_seq = dpss(seq_length,time_halfbandwidth)seq_length の、最初の round(2*time_halfbandwidth) 個の離散扁長回転楕円体列 (DPSS)、すなわちスレピアン列が返されます。
[ では、dps_seq,lambda] = dpss(seq_length,time_halfbandwidth)dps_seq における列ベクトルの周波数領域エネルギー集中率 lambda が返されます。この比率は、[–Fs/2,Fs/2] からの総エネルギーに対する、通過帯域 [–W,W] のエネルギー量を表し、変数 Fs はサンプル レートを表します。
[___] = dpss( では seq_length,time_halfbandwidth,num_seq)time_halfbandwidth に等しい時間-半帯域積をもつ最初の num_seq 個のスレピアン列が返されます。この関数は、エネルギー集中率の順にシーケンスを返します。
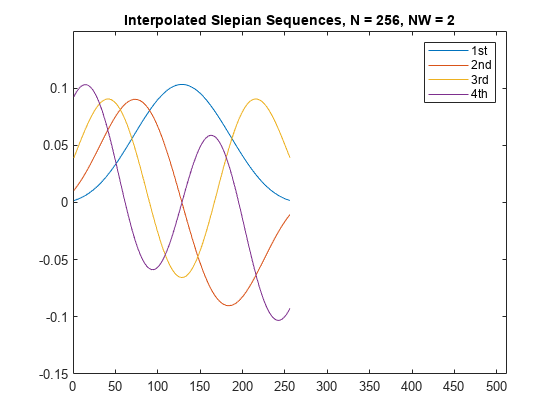
[___] = dpss( では、ユーザーの作成した DPSS のデータベースから、内挿を使用して DPSS が計算されます。seq_length,time_halfbandwidth,interp_method)dpsssave を使用して DPSS のデータベースを作成し、結果として得られる dpss.mat ファイルが MATLAB® 検索パスにあることを確認します。
[___] = dpss(___, では、データベース Ni)dpss.mat にある長さ Ni の DPSS から内挿が行われます。
[___] = dpss(___,"trace") では、DPSS の計算に使用される手法がコマンド ウィンドウに表示されます。表示される可能性のある手法としては、直接内挿、スプライン内挿や線形内挿などがあります。