このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
chirp
スイープ周波数の余弦信号
構文
説明
例
線形チャープ
瞬時周波数偏差が線形に変化するチャープを生成します。チャープは 1 kHz で 2 秒間サンプリングされています。瞬時周波数は、t = 0 では 0 であり、t = 1 秒で 250 Hz になります。
t = 0:1/1e3:2; y = chirp(t,0,1,250);
チャープのスペクトログラムを計算し、プロットします。時間分解能が 0.1 秒になるように信号をセグメントに分割します。隣接するセグメント間の 99% のオーバーラップ、および 0.85 のスペクトル漏れを指定します。
pspectrum(y,1e3,'spectrogram','TimeResolution',0.1, ... 'OverlapPercent',99,'Leakage',0.85)

2 次チャープ
瞬時周波数偏差が時間の 2 乗とともに変化するチャープを生成します。チャープは 1 kHz で 2 秒間サンプリングされています。瞬時周波数は、t = 0 では 100 Hz であり、t = 1 秒で 200 Hz になります。
t = 0:1/1e3:2;
y = chirp(t,100,1,200,'quadratic');チャープのスペクトログラムを計算し、プロットします。時間分解能が 0.1 秒になるように信号をセグメントに分割します。隣接するセグメント間の 99% のオーバーラップ、および 0.85 のスペクトル漏れを指定します。
pspectrum(y,1e3,'spectrogram','TimeResolution',0.1, ... 'OverlapPercent',99,'Leakage',0.85)
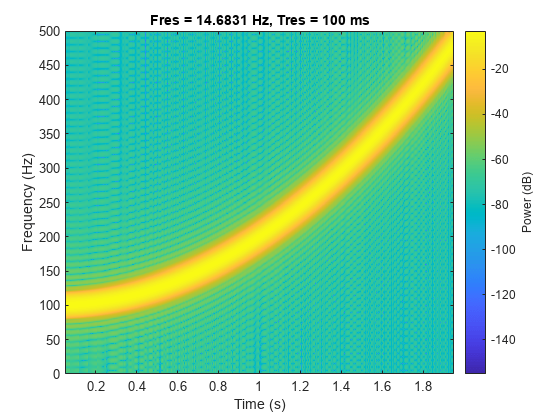
凸の 2 次チャープ
1 kHz で 2 秒間サンプリングされた凸の 2 次チャープを生成します。瞬時周波数は、t = 0 では 400 Hz であり、t = 1 秒で 300 Hz になります。
t = 0:1/1e3:2; fo = 400; f1 = 300; y = chirp(t,fo,1,f1,'quadratic',[],'convex');
チャープのスペクトログラムを計算し、プロットします。時間分解能が 0.1 秒になるように信号をセグメントに分割します。隣接するセグメント間の 99% のオーバーラップ、および 0.85 のスペクトル漏れを指定します。
pspectrum(y,1e3,'spectrogram','TimeResolution',0.1, ... 'OverlapPercent',99,'Leakage',0.85)
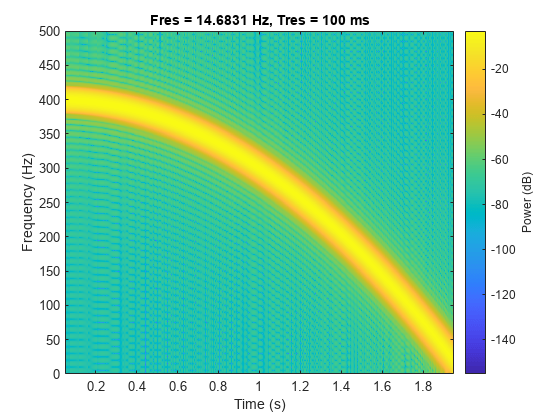
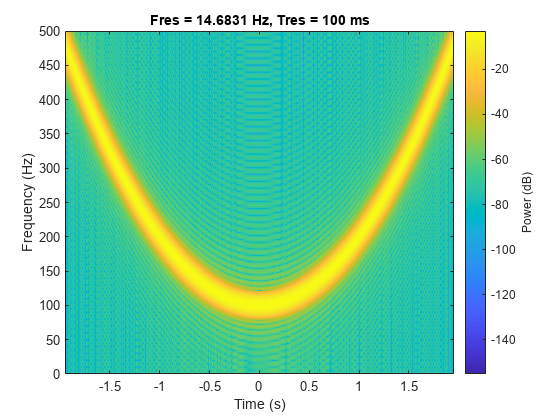
対称な凹の 2 次チャープ
1 kHz で 4 秒間サンプリングされた凹の 2 次チャープを生成します。瞬時周波数が、最小周波数 100 Hz、最大周波数 500 Hz のサンプリング間隔の中間点で対称となるように時間ベクトルを指定します。
t = -2:1/1e3:2; fo = 100; f1 = 200; y = chirp(t,fo,1,f1,'quadratic',[],'concave');
チャープのスペクトログラムを計算し、プロットします。時間分解能が 0.1 秒になるように信号をセグメントに分割します。隣接するセグメント間の 99% のオーバーラップ、および 0.85 のスペクトル漏れを指定します。
pspectrum(y,t,'spectrogram','TimeResolution',0.1, ... 'OverlapPercent',99,'Leakage',0.85)
対数チャープ
1 kHz で 10 秒間サンプリングされた対数チャープを生成します。瞬時周波数は、最初は 10 Hz で最後は 400 Hz になります。
t = 0:1/1e3:10;
fo = 10;
f1 = 400;
y = chirp(t,fo,10,f1,'logarithmic');チャープのスペクトログラムを計算し、プロットします。時間分解能が 0.2 秒になるように信号をセグメントに分割します。隣接するセグメント間の 99% のオーバーラップ、および 0.85 のスペクトル漏れを指定します。
pspectrum(y,t,'spectrogram','TimeResolution',0.2, ... 'OverlapPercent',99,'Leakage',0.85)
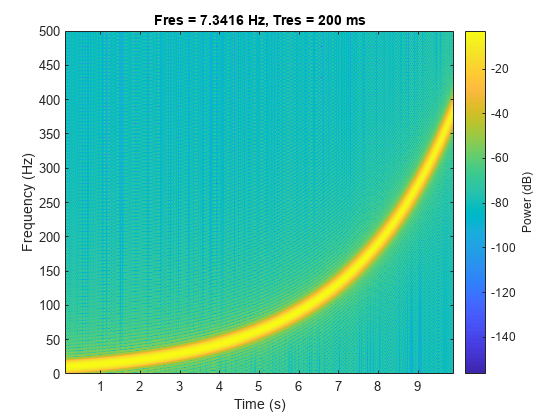
周波数軸に対数スケールを使用します。スペクトログラムは低周波において高い不確実性をもつ直線になります。
ax = gca;
ax.YScale = 'log';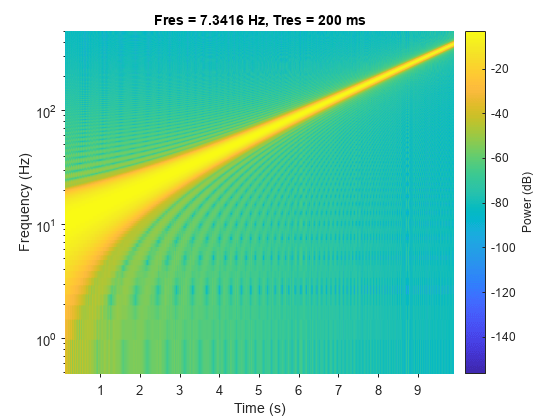
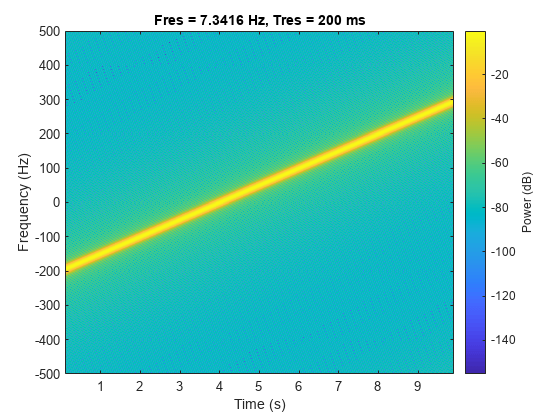
複素チャープ
1 kHz で 10 秒間サンプリングされた複素線形チャープを生成します。瞬時周波数は、最初は -200 Hz で最後は 300 Hz になります。初期位相はゼロです。
t = 0:1/1e3:10; fo = -200; f1 = 300; y = chirp(t,fo,t(end),f1,'linear',0,'complex');
チャープのスペクトログラムを計算し、プロットします。時間分解能が 0.2 秒になるように信号をセグメントに分割します。隣接するセグメント間の 99% のオーバーラップ、および 0.85 のスペクトル漏れを指定します。
pspectrum(y,t,'spectrogram','TimeResolution',0.2, ... 'OverlapPercent',99,'Leakage',0.85)

複素チャープに、等しいが の位相差をもつ実数部と虚数部があることを確認します。
x = chirp(t,fo,t(end),f1,'linear',0) + 1j*chirp(t,fo,t(end),f1,'linear',-90); pspectrum(x,t,'spectrogram','TimeResolution',0.2, ... 'OverlapPercent',99,'Leakage',0.85)
入力引数
t — 時間配列
ベクトル
時間配列。ベクトルとして指定します。
データ型: single | double
f0 — 時間 0 での瞬時周波数
0 (既定値) | Hz 単位の実数スカラー
時間 0 での初期瞬時周波数。実数スカラーとして Hz 単位で指定します。
データ型: single | double
t1 — 参照時間
1 (既定値) | 秒単位の正のスカラー
参照時間。秒単位の正のスカラーとして指定します。
データ型: single | double
f1 — 時間 t1 での瞬時周波数
100 (既定値) | Hz 単位の実数スカラー
時間 t1 での瞬時周波数。実数スカラーとして Hz 単位で指定します。
データ型: single | double
method — スイープ手法
'linear' (既定値) | 'quadratic' | 'logarithmic'
スイープ手法。'linear'、'quadratic'、または 'logarithmic' として指定します。
'linear'— 以下の式によって求められる瞬時周波数スイープ fi(t) が指定されます。ここで
また、f0 の既定値は 0 です。係数 β により、時間 t1 における望ましい周波数ブレークポイント f1 の維持が確保されます。
'quadratic'— 以下の式によって求められる瞬時周波数スイープ fi(t) が指定されます。ここで
また、f0 の既定値は 0 です。f0 > f1 (ダウンスイープ) の場合、既定の形状は凸になります。f0 < f1 (アップスイープ) の場合、既定の形状は凹になります。
'logarithmic'— 以下の式によって求められる瞬時周波数スイープ fi(t) が指定されます。ここで
また、f0 の既定値は 10–6 です。
phi — Initial phase
0 (既定値) | 度単位の正のスカラー
初期位相。正のスカラーとして度単位で指定します。
データ型: single | double
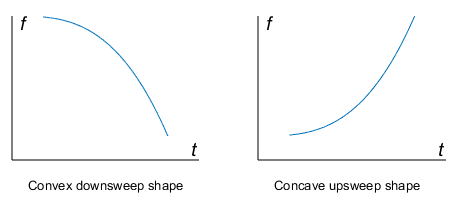
shape — 2 次チャープのスペクトログラム形状
'convex' | 'concave'
2 次チャープのスペクトログラム形状。'convex' または 'concave' として指定します。shape は正の周波数軸での放物線の形状を記述します。shape を指定しなかった場合は、f0 > f1 のダウンスイープでは 'convex' になり、f0 < f1 のアップスイープでは 'concave' になります。
cplx — 出力の実数/複素数
'real' (既定値) | 'complex'
出力の実数/複素数。'real' または 'complex' として指定します。
出力引数
y — スイープ周波数の余弦信号
ベクトル
ベクトルとして返されるスイープ周波数の余弦信号。
拡張機能
C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。
スレッドベースの環境
MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。
この関数は、スレッドベースの環境を完全にサポートします。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。
バージョン履歴
R2006a より前に導入
MATLAB コマンド
次の MATLAB コマンドに対応するリンクがクリックされました。
コマンドを MATLAB コマンド ウィンドウに入力して実行してください。Web ブラウザーは MATLAB コマンドをサポートしていません。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)