このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
確定的周期信号のパワーの測定
この例は、確定的な周期信号のパワーを測定する方法を示します。時間は連続ですが、周期的で確定的な信号は離散のパワー スペクトルを生成します。また、この例では、再代入手法を使用してパワー測定値を改善する方法についても説明します。
信号分類
通常、信号は、パワー信号、エネルギー信号、その他の信号の 3 つのカテゴリに分類されます。正弦波から生成される確定的な信号は、エネルギーが無限で平均パワーが有限の "パワー信号" の例です。ランダム信号の平均パワーも有限で、パワー信号に分類されます。過渡信号は、ゼロ振幅で開始および終了する "エネルギー信号" の例です。その他の信号には、パワー信号とエネルギー信号の特徴がありません。
単一正弦波の理論的なパワー
最初の例として、1 のピーク振幅と 128 Hz の周波数成分をもつ正弦波信号の平均パワーを推定します。
Fs = 1024; t = 0:1/Fs:1-(1/Fs); A = 1; F1 = 128; x = A*sin(2*pi*t*F1);
時間領域で信号の一部をプロットします。
idx = 1:128; plot(t(idx),x(idx)) ylabel('Amplitude') xlabel('Time (seconds)') axis tight grid
各複素正弦波の理論的な平均パワー (平均二乗) は で、この例では 0.25 または -6.02 dB です。したがって、正の周波数と負の周波数のパワーを考慮すると、平均パワーは になります。
power_theoretical = (A^2/4)*2
power_theoretical = 0.5000
dB 単位で、正の周波数に含まれるパワーを計算します。
pow2db(power_theoretical/2)
ans = -6.0206
単一正弦波のパワーの測定
信号の平均パワーを測定するには、periodogram を呼び出して 'power' オプションを指定します。
periodogram(x,hamming(length(x)),[],Fs,'centered','power') ylim([-10 -5.5])
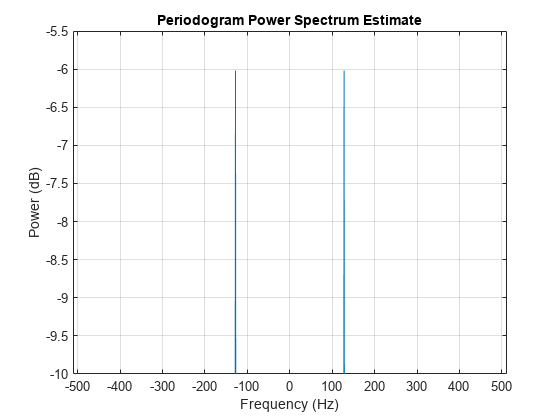
プロットの拡大部分からわかるように、各複素正弦波の平均パワーは約 -6 dB です。
PSD を使用した単一正弦波のパワーの推定
PSD 曲線の下の面積を "積分" しても、信号の平均パワーを計算できます。
periodogram(x,hamming(length(x)),[],Fs,'centered','psd')
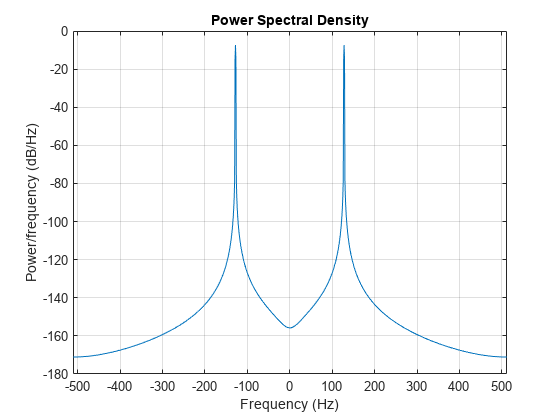
このプロットでは、スペクトル プロットのピークの高さは、パワー スペクトルのプロット時と異なります。高さが異なる理由は、パワー スペクトル密度 (PSD) の測定時に、曲線の下の面積 (平均パワーの測定値) が重要であるためです。この状態を検証するには、四角形近似を使って平均パワーを計算する関数 bandpower を使用して、曲線の下の面積を積分します。
[Pxx_hamming,F] = periodogram(x,hamming(length(x)),[],Fs,'psd'); power_freqdomain = bandpower(Pxx_hamming,F,'psd')
power_freqdomain = 0.5000
パーセバルの定理によると、正弦波の合計平均パワーは、時間領域と周波数領域において等しくなります。この事実を活用し、時間領域の信号を合計することによって、信号の推定合計平均パワーの値をチェックできます。
power_timedomain = sum(abs(x).^2)/length(x)
power_timedomain = 0.5000
複数正弦波の理論的なパワー
2 番目の例では、複数の周波数成分のエネルギーを含んでいる信号の合計平均パワーを推定します。ここでの周波数は、振幅 1.5 で DC、振幅 4 で 100 Hz、および振幅 3 で 200 Hz とします。
Fs = 1024; t = 0:1/Fs:1-(1/Fs); Ao = 1.5; A1 = 4; A2 = 3; F1 = 100; F2 = 200; x = Ao + A1*sin(2*pi*t*F1) + A2*sin(2*pi*t*F2);
信号の最初の 128 サンプルをプロットします。
idx = 1:128; plot(t(idx),x(idx)) grid ylabel('Amplitude') xlabel('Time (seconds)')
前の例と同様に、各複素正弦波の理論上の平均パワーは です。信号の DC 平均パワーは、一定で、 で求められるため、ピーク パワーと等しくなります。正の周波数および負の周波数のパワーを考慮すると、信号の合計平均パワーの値 (各高調波成分の平均パワーの合計) は になります。
power_theoretical = Ao^2 + (A1^2/4)*2 + (A2^2/4)*2
power_theoretical = 14.7500
dB 単位で各固有周波数成分の平均パワーを計算して、理論上の結果と以下の平均二乗スペクトル プロットが一致することを確認します。
pow2db([Ao^2 A1^2/4 A2^2/4])
ans = 1×3
3.5218 6.0206 3.5218
複数正弦波のパワーの測定
信号の平均パワーをもう一度測定するには、関数 periodogram を再度使用し、信号のパワー スペクトルを計算してプロットします。
periodogram(x,hamming(length(x)),[],Fs,'centered','power') ylim([0 7])
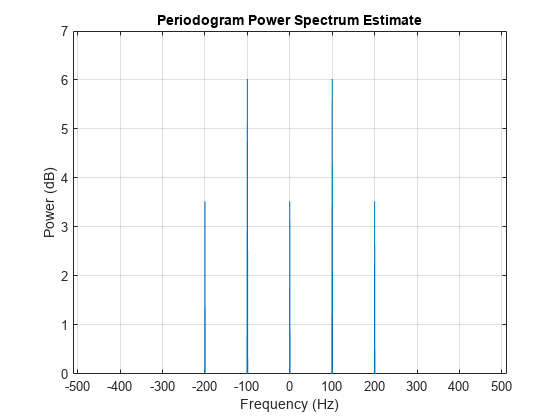
PSD を使用した複数正弦波のパワーの推定
最初の例と同様に、PSD 曲線の下の面積を "積分" し、信号の合計平均パワーを推定します。
periodogram(x,hamming(length(x)),[],Fs,'centered','psd')
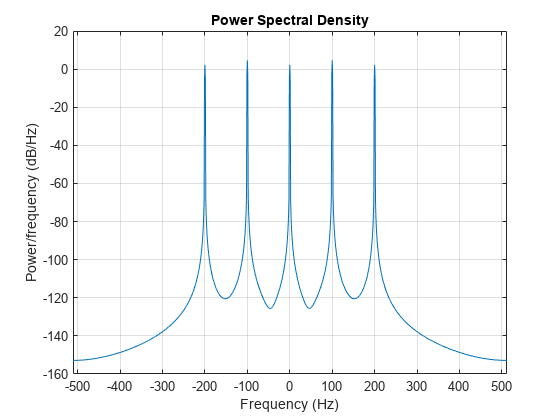
特定の周波数成分におけるスペクトル密度プロットのピークの高さは、パワー スペクトルのプロットと一致しない場合があります。この違いは、最初の例で示した理由によるものです。
[Pxx, F] = periodogram(x, hamming(length(x)),[],Fs,'centered','psd'); power_freqdomain = bandpower(Pxx,F,'psd')
power_freqdomain = 14.7500
また、信号の推定平均パワーを検証するには、パーセルの定理を呼び出し、時間領域で信号を合計します。
power_timedomain = sum(abs(x).^2)/length(x)
power_timedomain = 14.7500
パワー スペクトル、パワー スペクトル密度および ENBW の関係
パワー プロットとパワー スペクトル密度プロットのピークの高さは異なるものの、その比率は一定であることが見て取れます。
Pxx = periodogram(x,hamming(length(x)),[],Fs,'centered','psd'); Sxx = periodogram(x,hamming(length(x)),[],Fs,'centered','power'); plot(F,Sxx./Pxx) grid axis tight xlabel('Frequency (Hz)') title('Ratio of Power Spectrum to Power Spectral Density')
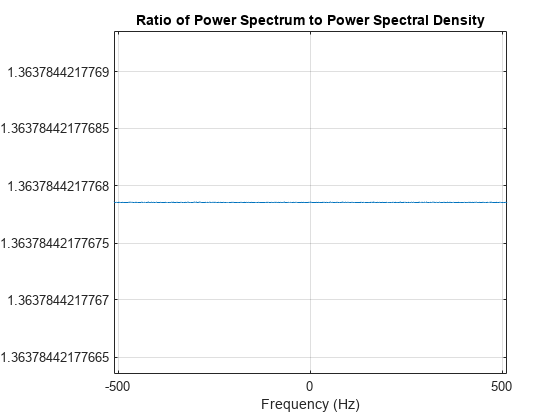
ratio = mean(Sxx./Pxx)
ratio = 1.3638
パワーとパワー スペクトル密度の比は、ウィンドウの両側等価ノイズ帯域幅 (ENBW) に関連しています。ウィンドウの関数 enbw、およびこれと対応するサンプル レートを入力引数として呼び出すことで、この比を直接計算することができます。
bw = enbw(hamming(length(x)),Fs)
bw = 1.3638
再割り当てされたピリオドグラムを使用した詳細なパワー測定
前の節では、ビンと一致した周波数をもつ 1 つ以上の正弦波からパワーが測定されました。信号の周波数がビンから外れた場合、ピーク パワー推定の精度は通常低下します。この影響を確認するため、1 秒間にわたる非整数のサイクル数をもつ正弦波を作成します。
Fs = 1024; t = 0:1/Fs:1-(1/Fs); A = 1; F = 20.4; x = A*sin(2*pi*F*t); nfft = length(x); power_theoretical = pow2db(A^2/4*2);
ハミング ウィンドウとフラット トップ ウィンドウを作成します。
w1 = hamming(length(x)); w2 = flattopwin(length(x));
ハミング ウィンドウを使用して、x のピリオドグラムを計算します。ピークを拡大します。
h1 = figure; stem(F,power_theoretical,'BaseValue',-50); [Pxx1,f1] = periodogram(x,w1,nfft,Fs,'power'); hold on plot(f1,pow2db(Pxx1),'+-') axis([0 40 -45 0]) legend('Theoretical','Periodogram') xlabel('Frequency (Hz)') ylabel('Power (dB)') title('Periodogram Power Spectrum Estimate') grid
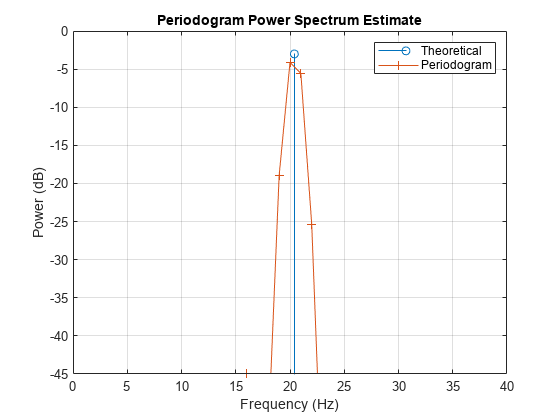
ピーク パワー推定値は理論上のピークを下回り、ピーク推定の周波数は実際の周波数と異なっています。
[Pmax,imax] = max(Pxx1); dPmax_w1 = pow2db(Pmax) - power_theoretical
dPmax_w1 = -1.1046
dFreq = f1(imax) - F
dFreq = -0.4000
ゼロ パディングを使用した振幅誤差の削減
このようなことが起きている理由を調べるために、より多数の FFT ビンを使用してピリオドグラムを計算します。
[Pxx2,f2] = periodogram(x,w1,100*nfft,Fs,'power'); figure stem(F,power_theoretical,'BaseValue',-50) hold on plot(f1,pow2db(Pxx1),'+') plot(f2,pow2db(Pxx2)) hold off axis([0 40 -40 0]) legend('Theoretical Peak','nfft = 1024','nfft = 102400') xlabel('Frequency (Hz)') ylabel('Power (dB)') title('Periodogram Power Spectrum Estimate') grid
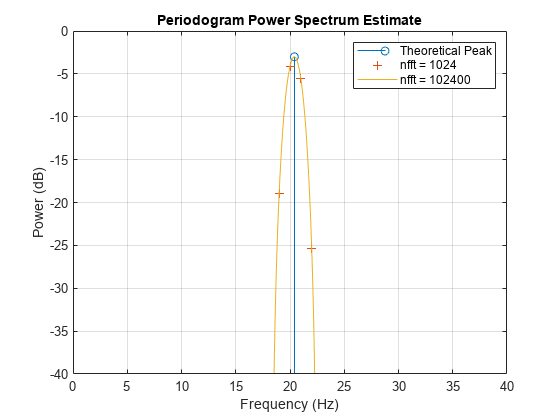
元のピリオドグラムではスペクトル ピークが 2 つのビンの間に位置しており、そのために推定されたピークが理論上のピークより下になっています。FFT ビンの数を増やすとスペクトルの画質は向上しますが、ピーク測定値を向上させる計算コストとしては高い可能性があります。
フラット トップ ウィンドウを使用した振幅誤差の削減
ピーク振幅をより正確に推定する別の方法として、別のウィンドウを使用できます。フラット トップ ウィンドウを使用して、x のピリオドグラムを計算します。
[Pxx,F1] = periodogram(x,w2,nfft,Fs,'power'); figure(h1) plot(F1,pow2db(Pxx)) legend('Theoretical','Hamming','Flat Top') hold off
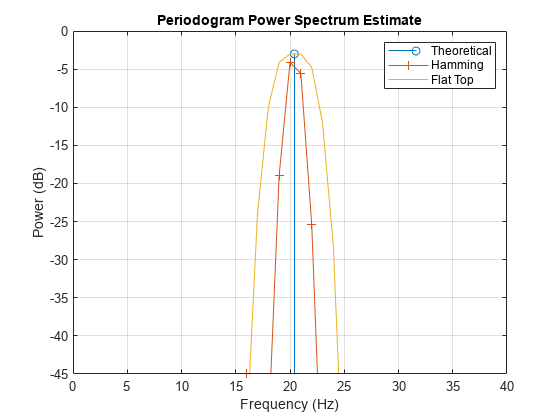
フラット トップ ウィンドウは幅が広く平坦です。これは、x が整数のサイクル数を含まない場合、理論値に近いピーク推定を生成するため、スペクトル ピークが正確にビン上にくるとは限らなくなります。
dPmax_w2 = pow2db(max(Pxx)) - power_theoretical
dPmax_w2 = -6.2007e-04
近接したピークを分離する場合、フラット トップ ウィンドウが生成する幅の広いピークは不利になる可能性があり、ここでも測定されたピークの周波数は理論上のピークの周波数と異なるものとなります。
再割り当てされたピリオドグラムを使用した振幅誤差の削減
今度は、periodogram に 'reassigned' フラグを追加します。ピリオドグラムの再割り当てでは、信号をエネルギーの中心に再度割り当てるために、通常は破棄される位相情報を使用します。この手順により、スペクトル推定をよりシャープにすることができます。再割り当てされた x のピリオドグラムをプロットし、ピークを拡大します。ハミング ウィンドウおよびフラット トップ ウィンドウを使用します。
[RPxx1,~,~,Fc1] = periodogram(x,w1,nfft,Fs,'power','reassigned'); [RPxx2,~,~,Fc2] = periodogram(x,w2,nfft,Fs,'power','reassigned'); stem(F,power_theoretical,'*','BaseValue',-40) hold on stem(Fc1,pow2db(RPxx1),'BaseValue',-50) stem(Fc2,pow2db(RPxx2),'BaseValue',-50) hold off legend('Theoretical','Hamming Reassignment','Flattop Reassignment') xlabel('Frequency (Hz)') ylabel('Power (dB)') title('Periodogram Power Spectrum Estimate') axis([19.5 21 -4 -2]) grid
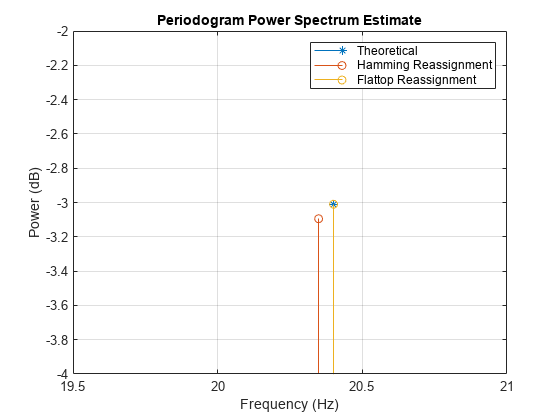
再割り当てされたパワーの推定値は、いずれのウィンドウの場合もより理論値に近づいていますが、フラット トップ ウィンドウの生成するピーク測定が最も優れています。
[RPxx1max,imax1] = max(RPxx1); [RPxx2max,imax2] = max(RPxx2); dPmax_reassign_w1 = pow2db(RPxx1max) - power_theoretical
dPmax_reassign_w1 = -0.0845
dPmax_reassign_w2 = pow2db(RPxx2max) - power_theoretical
dPmax_reassign_w2 = -1.1131e-05
再割り当てされたピリオドグラムを使用すると周波数推定値も改善しますが、ここでもフラット トップ ウィンドウの場合に最も優れた結果が得られています。
Fc1(imax1)-F
ans = -0.0512
Fc2(imax2)-F
ans = 5.6552e-04
参考
bandpower | enbw | periodogram | pow2db
