lsqnonlin
非線形最小二乗 (非線形データ適合) 問題を解く
構文
説明
非線形最小二乗ソルバー
以下の形式の非線形最小二乗曲線近似問題を解きます。
以下の制約に従います。
x、lb および ub はベクトルまたは行列とすることができます。行列引数を参照してください。
目的関数をスカラー値 (二乗和) として指定しないでください。lsqnonlin は次の "ベクトル" 値関数となる目的関数を必要とします。
x = lsqnonlin(fun,x0)x0 を開始点として、fun に記述する関数の二乗和の最小値を求めます。関数 fun は、値の二乗和ではなく値のベクトル (または配列) を返します。(アルゴリズムは fun(x) の要素の二乗和を暗黙的に計算します。)
メモ
追加パラメーターの受け渡し は必要に応じて他のパラメーターを関数 fun(x) へ渡す方法を説明します。
例
単純な指数関数の当てはめ
単純な指数減衰曲線をデータに当てはめます。
ノイズを含む指数減衰モデルからデータを生成します。モデルは次のとおりです。
ここで、 の範囲は 0 ~ 3、 は平均が 0、標準偏差が 0.05 の正規分布ノイズです。
rng default % for reproducibility d = linspace(0,3); y = exp(-1.3*d) + 0.05*randn(size(d));
問題は、データ (d、y) について、データに最も適合する指数減衰率の検出です。
指数減衰率の値 を使用して、その減衰率とデータをもつモデルとの差のベクトルを返す、無名関数を作成します。
fun = @(r)exp(-d*r)-y;
最適な減衰率の値を求めます。任意の初期推定 x0 = 4 を選択します。
x0 = 4; x = lsqnonlin(fun,x0)
Local minimum possible. lsqnonlin stopped because the final change in the sum of squares relative to its initial value is less than the value of the function tolerance.
x = 1.2645
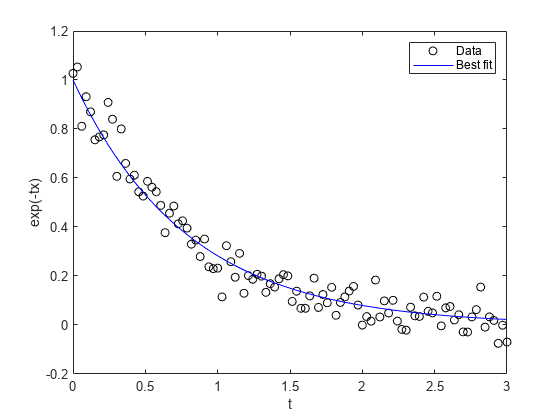
データおよび最適適合指数曲線をプロットします。
plot(d,y,'ko',d,exp(-x*d),'b-') legend('Data','Best fit') xlabel('t') ylabel('exp(-tx)')
範囲に制約のある問題の近似
適合パラメーターの一部が有界である場合の最適適合モデルを求めます。
次の関数のセンタリング およびスケーリング による最適な近似が、
次の標準正規密度に対して成り立つようにします。
データ点のベクトル t、およびこれらの点の対応する正規密度を作成します。
t = linspace(-4,4); y = 1/sqrt(2*pi)*exp(-t.^2/2);
センタリングおよびスケーリングした関数と、正規の y との差を評価する関数を作成します。ここで、x(1) はスケーリング 、x(2) はセンタリング です。
fun = @(x)x(1)*exp(-t).*exp(-exp(-(t-x(2)))) - y;
x0 = [1/2,0] から開始して、最適近似を求めます。スケーリング は 1/2 ~ 3/2、センタリング は -1 ~ 3 とします。
lb = [1/2,-1]; ub = [3/2,3]; x0 = [1/2,0]; x = lsqnonlin(fun,x0,lb,ub)
Local minimum possible. lsqnonlin stopped because the final change in the sum of squares relative to its initial value is less than the value of the function tolerance.
x = 1×2
0.8231 -0.2444
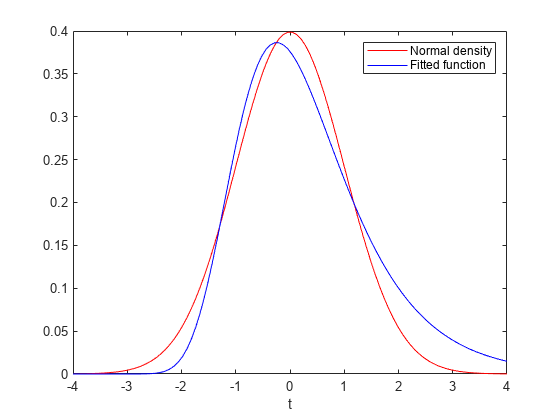
2 つの関数をプロットして、近似の質を確認します。
plot(t,y,'r-',t,fun(x)+y,'b-') xlabel('t') legend('Normal density','Fitted function')
線形制約を使用した最小二乗法
次の目的関数、二乗和について考えます。
この目的関数のコードは、この例の終わりに関数 myfun として掲載しています。
線形制約 に従ってこの関数を最小化します。この制約を として記述します。
A = [1 -1/2]; b = 0;
範囲 、、、および を設定します。
lb = [0 0]; ub = [2 4];
最適化プロセスを点 x0 = [0.3 0.4] から開始します。
x0 = [0.3 0.4];
この問題には線形等式制約がありません。
Aeq = []; beq = [];
最適化を実行します。
x = lsqnonlin(@myfun,x0,lb,ub,A,b,Aeq,beq)
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance.
x = 1×2
0.1695 0.3389
function F = myfun(x) k = 1:10; F = 2 + 2*k - exp(k*x(1)) - 2*exp(2*k*(x(2)^2)); end
非線形制約を使用した非線形最小二乗法
次の目的関数、二乗和について考えます。
この目的関数のコードは、この例の終わりに関数 myfun として掲載しています。
非線形制約 に従ってこの関数を最小化します。この非線形制約関数のコードは、この例の終わりに関数 nlcon として掲載しています。
範囲 、、、および を設定します。
lb = [0 0]; ub = [2 4];
最適化プロセスを点 x0 = [0.3 0.4] から開始します。
x0 = [0.3 0.4];
この問題には、線形制約がありません。
A = []; b = []; Aeq = []; beq = [];
最適化を実行します。
x = lsqnonlin(@myfun,x0,lb,ub,A,b,Aeq,beq,@nlcon)
Local minimum possible. Constraints satisfied. fmincon stopped because the size of the current step is less than the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance.
x = 1×2
0.2133 0.3266
function F = myfun(x) k = 1:10; F = 2 + 2*k - exp(k*x(1)) - 2*exp(2*k*(x(2)^2)); end function [c,ceq] = nlcon(x) ceq = []; c = sin(x(1)) - cos(x(2)); end
既定以外のオプションを使った非線形最小二乗
異なる lsqnonlin アルゴリズムを使用して、データ適合の問題の結果を比較します。
観測時間データ xdata および観測応答データ ydata について、次の形式のモデルが適合するパラメーター および を求めるものとします。
観測時間と応答を入力します。
xdata = ... [0.9 1.5 13.8 19.8 24.1 28.2 35.2 60.3 74.6 81.3]; ydata = ... [455.2 428.6 124.1 67.3 43.2 28.1 13.1 -0.4 -1.3 -1.5];
単純な指数減衰モデルを作成します。このモデルは、予測値と観測値の差のベクトルを計算します。
fun = @(x)x(1)*exp(x(2)*xdata)-ydata;
開始点 x0 = [100,-1] を使用してモデルを当てはめます。まず、既定の 'trust-region-reflective' アルゴリズムを使用します。
x0 = [100,-1]; options = optimoptions(@lsqnonlin,'Algorithm','trust-region-reflective'); x = lsqnonlin(fun,x0,[],[],options)
Local minimum possible. lsqnonlin stopped because the final change in the sum of squares relative to its initial value is less than the value of the function tolerance.
x = 1×2
498.8309 -0.1013
'levenberg-marquardt' アルゴリズムを使用する場合と違いがあるかどうか確認します。
options.Algorithm = 'levenberg-marquardt';
x = lsqnonlin(fun,x0,[],[],options)Local minimum possible. lsqnonlin stopped because the relative size of the current step is less than the value of the step size tolerance.
x = 1×2
498.8309 -0.1013
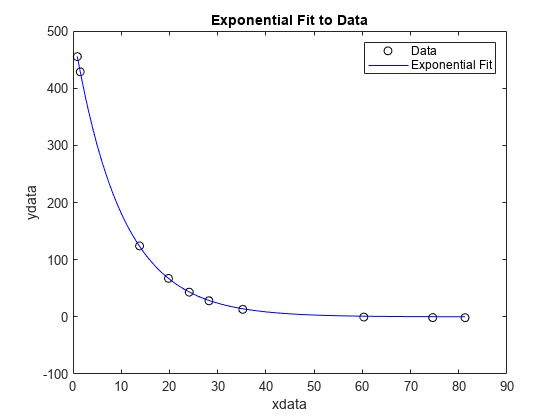
2 つのアルゴリズムで同じ解が得られています。解とデータをプロットします。
plot(xdata,ydata,'ko') hold on tlist = linspace(xdata(1),xdata(end)); plot(tlist,x(1)*exp(x(2)*tlist),'b-') xlabel xdata ylabel ydata title('Exponential Fit to Data') legend('Data','Exponential Fit') hold off
非線形最小二乗の解と残差のノルム
次を最小にする を求めます。
,
また、二乗和の最小値を求めます。
lsqnonlin は二乗和がユーザー関数で陽的に作成されて "いない" ことを想定しているため、lsqnonlin に渡す関数が以下のベクトル値関数を代わりに演算しなければなりません。
,
ここで、 ~ です (すなわち、 は 個の要素をもたなければなりません)。
関数 myfun (この例の終わりに掲載) が、10 要素のベクトル F を計算します。
点 x0 = [0.3,0.4] を開始点として、最小化点および最小値を求めます。
x0 = [0.3,0.4]; [x,resnorm] = lsqnonlin(@myfun,x0)
Local minimum possible. lsqnonlin stopped because the size of the current step is less than the value of the step size tolerance.
x = 1×2
0.2578 0.2578
resnorm = 124.3622
resnorm 出力は 2 乗残差ノルム、すなわち関数値の二乗和です。
次の関数は、ベクトル値目的関数を計算します。
function F = myfun(x) k = 1:10; F = 2 + 2*k-exp(k*x(1))-exp(k*x(2)); end
解法プロセスの検証
解法プロセスの発生時 (Display オプションを 'iter' に設定する)、およびその後 (output 構造体を調べる) の解法プロセスを検証します。
観測時間データ xdata および観測応答データ ydata について、次の形式のモデルが適合するパラメーター および を求めるものとします。
観測時間と応答を入力します。
xdata = ... [0.9 1.5 13.8 19.8 24.1 28.2 35.2 60.3 74.6 81.3]; ydata = ... [455.2 428.6 124.1 67.3 43.2 28.1 13.1 -0.4 -1.3 -1.5];
単純な指数減衰モデルを作成します。このモデルは、予測値と観測値の差のベクトルを計算します。
fun = @(x)x(1)*exp(x(2)*xdata)-ydata;
開始点 x0 = [100,-1] を使用してモデルを当てはめます。Display オプションを 'iter' に設定して、解法プロセスを検証します。output 構造体を取得し、解法プロセスの詳細情報を取得します。
x0 = [100,-1]; options = optimoptions('lsqnonlin','Display','iter'); [x,resnorm,residual,exitflag,output] = lsqnonlin(fun,x0,[],[],options);
Norm of First-order
Iteration Func-count Resnorm step optimality
0 3 359677 2.88e+04
Objective function returned Inf; trying a new point...
1 6 359677 11.6976 2.88e+04
2 9 321395 0.5 4.97e+04
3 12 321395 1 4.97e+04
4 15 292253 0.25 7.06e+04
5 18 292253 0.5 7.06e+04
6 21 270350 0.125 1.15e+05
7 24 270350 0.25 1.15e+05
8 27 252777 0.0625 1.63e+05
9 30 252777 0.125 1.63e+05
10 33 243877 0.03125 7.48e+04
11 36 243660 0.0625 8.7e+04
12 39 243276 0.0625 2e+04
13 42 243174 0.0625 1.14e+04
14 45 242999 0.125 5.1e+03
15 48 242661 0.25 2.04e+03
16 51 241987 0.5 1.91e+03
17 54 240643 1 1.04e+03
18 57 237971 2 3.36e+03
19 60 232686 4 6.04e+03
20 63 222354 8 1.2e+04
21 66 202592 16 2.25e+04
22 69 166443 32 4.05e+04
23 72 106320 64 6.68e+04
24 75 28704.7 128 8.31e+04
25 78 89.7947 140.674 2.22e+04
26 81 9.57381 2.02599 684
27 84 9.50489 0.0619927 2.27
28 87 9.50489 0.000462261 0.0114
Local minimum possible.
lsqnonlin stopped because the final change in the sum of squares relative to
its initial value is less than the value of the function tolerance.
出力構造体を検証し、解法プロセスの詳細情報を取得します。
output
output = struct with fields:
firstorderopt: 0.0114
iterations: 28
funcCount: 87
cgiterations: 0
algorithm: 'trust-region-reflective'
stepsize: 4.6226e-04
message: 'Local minimum possible....'
bestfeasible: []
constrviolation: []
比較のために、Algorithm オプションを 'levenberg-marquardt' に設定します。
options.Algorithm = 'levenberg-marquardt';
[x,resnorm,residual,exitflag,output] = lsqnonlin(fun,x0,[],[],options); First-order Norm of
Iteration Func-count Resnorm optimality Lambda step
0 3 359677 2.88e+04 0.01
Objective function returned Inf; trying a new point...
1 13 340761 3.91e+04 100000 0.280777
2 16 304661 5.97e+04 10000 0.373146
3 21 297292 6.55e+04 1e+06 0.0589933
4 24 288240 7.57e+04 100000 0.0645444
5 28 275407 1.01e+05 1e+06 0.0741266
6 31 249954 1.62e+05 100000 0.094571
7 36 245896 1.35e+05 1e+07 0.0133606
8 39 243846 7.26e+04 1e+06 0.0094431
9 42 243568 5.66e+04 100000 0.0082162
10 45 243424 1.61e+04 10000 0.00777935
11 48 243322 8.8e+03 1000 0.0673933
12 51 242408 5.1e+03 100 0.675209
13 54 233628 1.05e+04 10 6.59804
14 57 169089 8.51e+04 1 54.6992
15 60 30814.7 1.54e+05 0.1 196.939
16 63 147.496 8e+03 0.01 129.795
17 66 9.51503 117 0.001 9.96069
18 69 9.50489 0.0714 0.0001 0.080486
19 72 9.50489 5.23e-05 1e-05 5.07043e-05
Local minimum possible.
lsqnonlin stopped because the relative size of the current step is less than
the value of the step size tolerance.
'levenberg-marquardt' の方が少ない反復回数で収束していますが、関数評価の回数はほぼ同じです。
output
output = struct with fields:
iterations: 19
funcCount: 72
stepsize: 5.0704e-05
cgiterations: []
firstorderopt: 5.2319e-05
algorithm: 'levenberg-marquardt'
message: 'Local minimum possible....'
bestfeasible: []
constrviolation: []
入力引数
fun — 二乗和が最小化される関数
関数ハンドル | 関数名
二乗和が最小化される関数。関数ハンドルまたは関数名として指定します。'interior-point' アルゴリズムの場合、fun は関数ハンドルである必要があります。fun は、配列 x を受け、x で評価される目的関数である配列 F を返す関数です。
メモ:
二乗和を明示的に形成すべきではありません。その代わりに、関数が関数値のベクトルを戻すべきです。詳細については、例を参照してください。
関数 fun はファイルへの関数ハンドルとして指定することができます。
x = lsqnonlin(@myfun,x0)
ここで myfun は次のような MATLAB® 関数です。
function F = myfun(x) F = ... % Compute function values at x
fun は無名関数の関数ハンドルにもなります。
x = lsqnonlin(@(x)sin(x.*x),x0);
lsqnonlin は、x0 引数の形式で x を目的関数に渡します。たとえば、x0 が 5 行 3 列の配列の場合、lsqnonlin は 5 行 3 列の配列として x を fun に渡します。
ヤコビアンも計算することができ、"さらに" 下式で設定された 'SpecifyObjectiveGradient' オプションが true である場合を考えます。
options = optimoptions('lsqnonlin','SpecifyObjectiveGradient',true)
関数 fun は 2 番目の出力引数に x でのヤコビ値 J (行列) を返さなければなりません。nargout の値を確認することで、1 つの出力引数のみの場合 (最適化アルゴリズムが J ではなく F の値のみを必要とする場合)、fun が呼び出されるときに J の演算を避けることができます。
function [F,J] = myfun(x) F = ... % Objective function values at x if nargout > 1 % Two output arguments J = ... % Jacobian of the function evaluated at x end
fun が m 個の成分をもつ配列を返し、x が n 個の要素をもつ場合 (ここで、n は x0 の要素数)、ヤコビアン J は m 行 n 列の行列になります。ここで、J(i,j) は F(i) の x(j) における偏導関数です。(ヤコビアン J は、F の勾配の転置であることに注意してください。)
例: @(x)cos(x).*exp(-x)
データ型: char | function_handle | string
x0 — 初期点
実数ベクトル | 実数配列
初期点。実数ベクトルまたは実数配列として指定されます。ソルバーは、x0 の要素数および x0 のサイズを使用して、fun が受け入れる変数の数およびサイズを決定します。
例: x0 = [1,2,3,4]
データ型: double
lb — 下限
実数ベクトル | 実数配列
下限。実数ベクトルまたは実数配列として指定されます。x0 の要素数と lb の要素数が等しい場合、lb は次を指定します。
x(i) >= lb(i) (すべての i について)
numel(lb) < numel(x0) の場合、lb は次を指定します。
x(i) >= lb(i) (1 <= i <= numel(lb))
lb の要素数が x0 より少ない場合、ソルバーは警告を生成します。
例: x のすべての成分が正であることを指定するには、lb = zeros(size(x0)) を使用します。
データ型: double
ub — 上限
実数ベクトル | 実数配列
実数ベクトルまたは実数配列として指定される上限です。x0 の要素数と ub の要素数が等しい場合、ub は次を指定します。
x(i) <= ub(i) (すべての i について)
numel(ub) < numel(x0) の場合、ub は次を指定します。
x(i) <= ub(i) (1 <= i <= numel(ub))
ub の要素数が x0 より少ない場合、ソルバーは警告を生成します。
例: x のすべての成分が 1 未満であることを指定するには、ub = ones(size(x0)) を使用します。
データ型: double
A — 線形不等式制約
実数行列
実数行列として指定される線形不等式制約です。A は M 行 N 列の行列で、M は不等式の数、N は変数の数 (x0 の要素数) です。大規模な問題の場合は、A をスパース行列として渡します。
A は M 個の線形不等式を符号化します。
A*x <= b,
ここで、x は N 個の変数 x(:) の列ベクトル、b は M 個の要素をもつ列ベクトルです。
たとえば、次の不等式を考えてみましょう。
x1 + 2x2 ≤ 10
3x1 + 4x2 ≤ 20
5x1 + 6x2 ≤ 30,
次の制約を入力することによって、不等式を指定します。
A = [1,2;3,4;5,6]; b = [10;20;30];
例: x の成分の和が 1 以下であることを指定するには、A = ones(1,N) と b = 1 を使用します。
データ型: double
b — 線形不等式制約
実数ベクトル
実数ベクトルで指定される線形不等式制約です。b は、行列 A に関連する M 要素ベクトルです。b を行ベクトルとして渡す場合、ソルバーは b を列ベクトル b(:) に内部的に変換します。大規模な問題の場合は、b をスパース ベクトルとして渡します。
b は M 個の線形不等式を符号化します。
A*x <= b,
ここで、x は N 個の変数 x(:) の列ベクトル、A は M 行 N 列の行列です。
たとえば、次の不等式を考えてみましょう。
x1 + 2x2 ≤ 10
3x1 + 4x2 ≤ 20
5x1 + 6x2 ≤ 30.
次の制約を入力することによって、不等式を指定します。
A = [1,2;3,4;5,6]; b = [10;20;30];
例: x の成分の和が 1 以下であることを指定するには、A = ones(1,N) と b = 1 を使用します。
データ型: double
Aeq — 線形等式制約
実数行列
実数行列として指定される線形等式制約です。Aeq は Me 行 N 列の行列で、Me は等式の数、N は変数の数 (x0 の要素数) です。大規模な問題の場合は、Aeq をスパース行列として渡します。
Aeq は Me 個の線形等式を符号化します。
Aeq*x = beq,
ここで、x は N 個の変数 x(:) の列ベクトル、beq は Me 個の要素をもつ列ベクトルです。
たとえば、次の不等式を考えてみましょう。
x1 + 2x2 + 3x3 = 10
2x1 + 4x2 + x3 = 20,
次の制約を入力することによって、不等式を指定します。
Aeq = [1,2,3;2,4,1]; beq = [10;20];
例: x の成分の和が 1 であることを指定するには、Aeq = ones(1,N) と beq = 1 を使用します。
データ型: double
beq — 線形等式制約
実数ベクトル
実数ベクトルで指定される線形等式制約です。beq は、行列 Aeq に関連する Me 要素ベクトルです。beq を行ベクトルとして渡す場合、ソルバーは beq を列ベクトル beq(:) に内部的に変換します。大規模な問題の場合は、beq をスパース ベクトルとして渡します。
beq は Me 個の線形等式を符号化します。
Aeq*x = beq,
ここで、x は N 個の変数 x(:) の列ベクトル、Aeq は Me 行 N 列の行列です。
たとえば、次の等式を考えてみましょう。
x1 + 2x2 + 3x3 = 10
2x1 + 4x2 + x3 = 20.
次の制約を入力することによって、等式を指定します。
Aeq = [1,2,3;2,4,1]; beq = [10;20];
例: x の成分の和が 1 であることを指定するには、Aeq = ones(1,N) と beq = 1 を使用します。
データ型: double
nonlcon — 非線形制約
関数ハンドル
非線形制約。関数ハンドルとして指定されます。nonlcon は、ベクトルまたは配列 x を受け、2 つの配列 c(x) および ceq(x) を返す関数です。
c(x)は、xでの非線形不等式制約の配列です。lsqnonlinは次の条件を満たそうとします。cのすべてのエントリに対してc(x) <= 0。(1) ceq(x)は、xでの非線形等式制約の配列です。lsqnonlinは次の条件を満たそうとします。ceqのすべてのエントリに対してceq(x) = 0。(2)
たとえば、
x = lsqnonlin(@myfun,x0,lb,ub,A,b,Aeq,beq,@mycon,options)
ここで mycon は次のような MATLAB 関数です。
function [c,ceq] = mycon(x) c = ... % Compute nonlinear inequalities at x. ceq = ... % Compute nonlinear equalities at x.
SpecifyConstraintGradient オプションが true である場合、options = optimoptions('lsqnonlin','SpecifyConstraintGradient',true)
nonlcon は 3 番目および 4 番目の出力引数に c(x) のヤコビアン GC および ceq(x) のヤコビアン GCeq を返さなければなりません。ベクトル関数 F(x) のヤコビアン G(x) は以下です。
GC と GCeq はスパースか密である可能性があります。GC か GCeq が大きく、比較的非零の項目が少ない場合は、それらをスパース行列として使用して、'interior-point' アルゴリズム内の実行時間とメモリを節約します。詳細については、非線形制約を参照してください。
データ型: function_handle
options — 最適化オプション
optimoptions の出力 | optimset によって返される構造体
最適化オプション。optimoptions の出力、または optimset によって返される構造体として指定されます。
いくつかのオプションはすべてのアルゴリズムに適用することができ、その他のオプションは特定のアルゴリズムに関連します。詳細については、最適化オプション リファレンスを参照してください。
一部のオプションは、optimoptions に表示されません。このようなオプションは、次の表ではイタリックで示されています。詳細については、最適化オプションの表示を参照してください。
| すべてのアルゴリズム | |
|
アルゴリズムの選択の詳細については、アルゴリズムの選択を参照してください。 |
CheckGradients | ユーザー設定の導関数 (目的関数または制約の勾配) と有限差分による導関数とを比較します。選択肢は、
|
| Diagnostics | 最小化または計算する関数に関する情報を表示します。選択肢は、 |
| DiffMaxChange | 有限差分勾配を計算する場合に変数内で生じる最大変化量です (正のスカラー)。既定値は |
| DiffMinChange | 有限差分勾配を計算する場合に変数内で生じる最小変化量です (正のスカラー)。既定値は |
| 表示レベル (反復表示を参照):
|
FiniteDifferenceStepSize | 有限差分のスカラーまたはベクトルのステップ サイズ ファクター。
sign′(0) = 1 を除き sign′(x) = sign(x) です。中心有限差分法では
FiniteDifferenceStepSize はベクトルに拡張します。既定値は、前進有限差分法では sqrt(eps)、中心有限差分法では eps^(1/3) です。
|
FiniteDifferenceType | 勾配推定に使用される有限差分は アルゴリズムは有限差分の両方のタイプを推定するとき、範囲に注意深く従います。そのためたとえば、forward ではなく、backward を選択すると、範囲外の点を計算しないようにすることができます。
|
| 関数値に関する終了許容誤差 (非負のスカラー)。既定値は
|
| FunValCheck | 関数値が有効かどうかをチェックします。 |
| 関数評価の最大許容回数 (非負の整数)。既定の値は
|
| 反復の最大許容回数 (非負の整数)。既定の値は、
|
OptimalityTolerance | 1 次の最適性に関する終了許容誤差 (非負のスカラー)。既定値は 内部的に、
|
OutputFcn | 各反復で最適化関数が呼び出すユーザー定義の関数を 1 つ以上指定します。関数ハンドルか、関数ハンドルの cell 配列を渡します。既定の設定はなし ( |
| アルゴリズムが実行中のさまざまな進行状況の測定値をプロットします。事前定義されたプロットから選択するか、独自のコードを記述してください。名前、関数ハンドル、または名前か関数ハンドルの cell 配列を渡します。カスタム プロット関数の場合は、関数ハンドルを渡します。既定の設定はなし (
カスタムのプロット関数は、出力関数と同じ構文を使用します。詳細については、Optimization Toolbox の出力関数と出力関数とプロット関数の構文を参照してください。
|
SpecifyObjectiveGradient |
|
|
|
| 典型的な |
UseParallel |
|
| 信頼領域 Reflective 法アルゴリズム | |
JacobianMultiplyFcn | ヤコビ乗算関数。関数ハンドルとして指定されます。大規模構造化問題に対して、この関数は実際に W = jmfun(Jinfo,Y,flag) ここで、 W = jmfun(Jinfo,Y,flag,xdata) ここで、 データ [F,Jinfo] = fun(x)
% or [F,Jinfo] = fun(x,xdata)
どの場合でも、 メモ:
同様の例は 密に構造化されたヘッシアンと線形等式を使用した最小化 と 線形最小二乗付きヤコビ乗算関数 を参照してください。
|
| JacobPattern | 有限差分に対するヤコビ スパース パターン。
構造が不明であれば、 |
| MaxPCGIter | PCG (前処理付き共役勾配) 法の反復の最大回数です (正のスカラー)。既定値は |
| PrecondBandWidth | PCG に対する前提条件子の帯域幅の上限 (非負の整数)。既定の |
SubproblemAlgorithm | 反復ステップの計算方法を定義します。既定の設定である |
| TolPCG | PCG 反復に関する終了許容誤差 (正のスカラー)。既定値は |
| レーベンバーグ・マルカート法アルゴリズム | |
| InitDamping | レーベンバーグ・マルカート パラメーターの初期値 (正のスカラー)。既定値は |
| ScaleProblem |
|
| 内点法アルゴリズム | |
BarrierParamUpdate |
このオプションは、ソルバーの速度と収束性に影響が及びますが、その影響の予測は困難です。 |
ConstraintTolerance | 制約違反に関する許容誤差 (非負のスカラー)。既定値は
|
| InitBarrierParam | 初期境界値 (正のスカラー)。既定の |
SpecifyConstraintGradient | ユーザーにより定義される非線形制約関数に対する勾配。既定の
|
SubproblemAlgorithm | 反復ステップの計算方法を定義します。
|
例: options = optimoptions('lsqnonlin','FiniteDifferenceType','central')
problem — 問題構造体
構造体
次のフィールドをもつ構造体として指定される問題構造体です。
| フィールド名 | エントリ |
|---|---|
| 目的関数 |
| x の初期点 |
| 線形不等式制約の行列 |
| 線形不等式制約のベクトル |
| 線形等式制約の行列 |
| 線形等式制約のベクトル |
lb | 下限のベクトル |
ub | 上限のベクトル |
| 非線形制約関数 |
| 'lsqnonlin' |
| optimoptions で作成されたオプション |
problem 構造体では、少なくとも objective、x0、solver、および options フィールドを指定しなければなりません。
データ型: struct
出力引数
x — 解
実数ベクトル | 実数配列
実数ベクトルまたは実数配列として返される解です。x のサイズは、x0 のサイズと同じです。通常、exitflag が正の場合、x は問題に対する局所的な解になります。解の質の詳細については、ソルバーが成功する場合を参照してください。
resnorm — 残差の 2 乗ノルム。
非負の実数
残差の 2 乗ノルム。非負の実数として返されます。resnorm は、x における残差の二乗した 2 ノルム (sum(fun(x).^2)) です。
residual — 解での目的関数の値
配列
解での目的関数の値。配列として返されます。一般的に、residual = fun(x) になります。
exitflag — ソルバーの停止理由
整数
ソルバーの停止理由。整数として返されます。
| 関数が解 |
|
|
| 残差の変化が指定された許容誤差を下回っています。 |
| 探索方向の相対振幅がステップの許容誤差を下回っています。 |
| 反復回数が |
| プロット関数または出力関数がソルバーを停止させたことを示します。 |
| 実行可能点が検出されませんでした。範囲 |
output — 最適化プロセスに関する情報
構造体
最適化プロセスに関する情報。次のフィールドをもつ構造体として返されます。
firstorderopt | 1 次の最適性の尺度 |
iterations | 実行した反復回数 |
funcCount | 関数評価回数です。 |
cgiterations | PCG 法での合計反復回数 ( |
stepsize |
|
constrviolation | 制約関数の最大値 ( |
bestfeasible | 検出された最適 (最小目的関数) 実行可能点 (
実行可能点が見つからなかった場合は、
|
algorithm | 使用される最適化アルゴリズム |
message | 終了メッセージ |
jacobian — 解におけるヤコビアン
実数行列
解におけるヤコビアン。実数行列として返されます。jacobian(i,j) は、解 x での x(j) に関する fun(i) の偏導関数です。
解にアクティブな制約条件がある問題では、jacobian は信頼区間の推定には有用ではありません。
制限
信頼領域 Reflective 法アルゴリズムは劣決定システムを扱いません。方程式の数、つまり F の行数が少なくとも変数の数と同じである必要があります。劣決定の場合、
lsqnonlinはレーベンバーグ・マルカート法アルゴリズムを使用します。lsqnonlinは複素数値問題を直接解くことができます。制約は複素数値に対して意味を持たないことに注意してください。なぜなら、複素数はきちんと順序付けされておらず、ある複素数値が他の複素数値より大きいか小さいかを問うことは無意味だからです。範囲制約を使用した複素数問題では、変数を実数部と虚数部に分けます。複素数データに'interior-point'アルゴリズムを使用しないでください。詳細については、複素数値データへのモデルの当てはめを参照してください。信頼領域 Reflective 法の前処理付き共役勾配法で使用される前提条件子の計算では、その計算の前に JTJ (J はヤコビ行列) を作成します。そのため多くの非ゼロ要素をもつ J の行は、密行列の積 JTJ に近い結果になり、大規模な問題についてはかなりのコストを要する解法プロセスになる場合があります。
x の構成要素に上限 (または下限) がない場合、
lsqnonlinでは非常に大きい任意の正の値 (下限に対しては負の値) を設定する代わりに、inf(下限に対しては-inf) をub(またはlb) の対応する構成要素に設定する方がより適切です。
lsqnonlin、lsqcurvefit、fsolve の信頼領域 Reflective 法アルゴリズムは、fun でヤコビアンを計算せずに、あるいはヤコビ スパース パターンを提示せずに、小規模から中規模の問題で使用できます。(これは、ヘッシアンの計算やヘッセ スパース パターンの入力なしで、fmincon または fminunc を使用する場合にも適用されます。) 小、中規模問題とは、どのくらい小さいのでしょうか。絶対的な答えはありません。ご利用のコンピューター システムの構成における仮想メモリ量によって異なるからです。
m 個の方程式と n 個の未知数の問題を考えてみましょう。コマンド J = sparse(ones(m,n)) が Out of memory エラーを引き起こす場合は、間違いなく大きな問題が発生しています。エラーが発生しない場合でも、問題の規模が大きすぎる場合があります。判定するには、問題を実行して MATLAB がシステムで使用可能な仮想メモリ内で実行されるかどうかを確認します。
アルゴリズム
レーベンバーグ・マルカート法および信頼領域 Reflective 法は、fsolve にも使用される非線形最小二乗アルゴリズムに基づいています。
既定の信頼領域 Reflective 法アルゴリズムは部分空間の信頼領域法であり、[1] および [2] で説明する interior-reflective ニュートン法に基づいています。各反復は、前処理付き共役勾配 (PCG) 法を使用する大型線形システムの近似解を伴います。詳細については、信頼領域 Reflective 法の最小二乗を参照してください。
レーベンバーグ・マルカート法は [4]、[5]、[6] の参考文献で説明されています。詳細については、レーベンバーグ・マルカート法を参照してください。
'interior-point' アルゴリズムは fmincon 'interior-point' アルゴリズムにいくつかの変更を加えて使用します。詳細については、制約付き最小二乗法に合わせて変更された fmincon アルゴリズムを参照してください。
代替機能
アプリ
[最適化] ライブ エディター タスクが lsqnonlin にビジュアル インターフェイスを提供します。
参照
[1] Coleman, T.F. and Y. Li. “An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds.” SIAM Journal on Optimization, Vol. 6, 1996, pp. 418–445.
[2] Coleman, T.F. and Y. Li. “On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds.” Mathematical Programming, Vol. 67, Number 2, 1994, pp. 189–224.
[3] Dennis, J. E. Jr. “Nonlinear Least-Squares.” State of the Art in Numerical Analysis, ed. D. Jacobs, Academic Press, pp. 269–312.
[4] Levenberg, K. “A Method for the Solution of Certain Problems in Least-Squares.” Quarterly Applied Mathematics 2, 1944, pp. 164–168.
[5] Marquardt, D. “An Algorithm for Least-squares Estimation of Nonlinear Parameters.” SIAM Journal Applied Mathematics, Vol. 11, 1963, pp. 431–441.
[6] Moré, J. J. “The Levenberg-Marquardt Algorithm: Implementation and Theory.” Numerical Analysis, ed. G. A. Watson, Lecture Notes in Mathematics 630, Springer Verlag, 1977, pp. 105–116.
[7] Moré, J. J., B. S. Garbow, and K. E. Hillstrom. User Guide for MINPACK 1. Argonne National Laboratory, Rept. ANL–80–74, 1980.
[8] Powell, M. J. D. “A Fortran Subroutine for Solving Systems of Nonlinear Algebraic Equations.” Numerical Methods for Nonlinear Algebraic Equations, P. Rabinowitz, ed., Ch.7, 1970.
拡張機能
C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。
lsqcurvefitとlsqnonlinは、codegen(MATLAB Coder) 関数または MATLAB Coder™ アプリを使用したコード生成をサポートしています。コードを生成するには MATLAB Coder ライセンスが必要です。ターゲット ハードウェアは、標準的な倍精度浮動小数点計算をサポートしていなければなりません。単精度計算や固定小数点計算のコードは生成できません。
コード生成ターゲットは、MATLAB ソルバーと同じ数学カーネル ライブラリを使用しません。そのため、コード生成解法は、特に、条件付けが不十分な問題の場合に、ソルバー解法と異なる可能性があります。
生成用のコードはすべて、MATLAB コードでなければなりません。特に、カスタム ブラックボックス関数を
lsqcurvefitまたはlsqnonlinの目的関数として使用することはできません。coder.cevalを使用して、C または C++ でコード化されたカスタム関数を評価することはできます。ただし、そのカスタム関数は MATLAB 関数内で呼び出さなければなりません。lsqcurvefitおよびlsqnonlinのコード生成は、現在、線形制約または非線形制約をサポートしていません。lsqcurvefitとlsqnonlinは、コード生成用のproblem引数をサポートしていません。[x,fval] = lsqnonlin(problem) % Not supported目的関数は、string や文字の名前ではなく、関数ハンドルを使用して指定しなければなりません。
x = lsqnonlin(@fun,x0,lb,ub,options) % Supported % Not supported: lsqnonlin('fun',...) or lsqnonlin("fun",...)
すべての入力行列
lbとubが、密 (非スパース) でなければなりません。関数fullを使用することで、スパース行列を非スパースに変換できます。lb引数とub引数は、x0引数と同じ数のエントリを持つか、空の[]でなければなりません。ターゲット ハードウェアが無限境界をサポートしていない場合は、
optim.coder.infboundを使用します。組み込みプロセッサを使用する高度なコード最適化には、Embedded Coder® ライセンスも必要です。
lsqcurvefitまたはlsqnonlin用のオプションを含め、それらをoptimoptionsを使用して指定しなければなりません。オプションにはAlgorithmオプションを含め、'levenberg-marquardt'に設定しなければなりません。options = optimoptions('lsqnonlin','Algorithm','levenberg-marquardt'); [x,fval,exitflag] = lsqnonlin(fun,x0,lb,ub,options);
コード生成では次のオプションをサポートしています。
Algorithm—'levenberg-marquardt'でなければなりませんFiniteDifferenceStepSizeFiniteDifferenceTypeFunctionToleranceMaxFunctionEvaluationsMaxIterationsSpecifyObjectiveGradientStepToleranceTypicalX
生成コードでは、オプションに対して限られたエラー チェックしか行われません。オプションの更新方法として、ドット表記ではなく、
optimoptionsを使用することを推奨します。opts = optimoptions('lsqnonlin','Algorithm','levenberg-marquardt'); opts = optimoptions(opts,'MaxIterations',1e4); % Recommended opts.MaxIterations = 1e4; % Not recommended
オプションはファイルから読み込まないでください。そうした場合、コード生成に失敗することがあります。代わりに、コード内でオプションを作成してください。
通常、サポートされていないオプションを指定すると、コード生成の際にそのオプションは暗黙的に無視されます。ただし、ドット表記を使用してプロット関数や出力関数を指定すると、コード生成でエラーが発生することがあります。信頼性を確保するために、サポートされているオプションのみを指定してください。
出力関数とプロット関数はサポートされていないため、ソルバーは終了フラグ –1 を返しません。
例については、lsqcurvefit または lsqnonlin の用のコード生成を参照してください。
自動並列サポート
Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。
並列実行するには、'UseParallel' オプションを true に設定します。
options = optimoptions('solvername','UseParallel',true)
詳細については、Optimization Toolbox での並列計算の使用を参照してください。
バージョン履歴
R2006a より前に導入R2023b: JacobianMultiplyFcn は任意のデータ型を受け入れる
JacobianMultiplyFcn オプションの構文は次のとおりです。
W = jmfun(Jinfo, Y, flag)
MATLAB が関数 jmfun に渡す Jinfo データに、任意のデータ型を使用できるようになりました。たとえば、Jinfo を構造体にすることが可能になりました。以前のリリースでは、Jinfo は標準の double 配列にする必要がありました。
Jinfo データは目的関数の 2 番目の出力です。
[F,Jinfo] = myfun(x)
R2023b: CheckGradients オプションは削除予定
CheckGradients オプションは将来のリリースで削除される予定です。目的関数または非線形制約関数の 1 次導関数を確認するには、関数 checkGradients を使用します。
R2023a: 線形制約と非線形制約のサポート
lsqnonlin は、線形制約と非線形制約の両方をサポートするようになりました。制約を満たすことができるように、ソルバーは fmincon の "interior-point" アルゴリズムを使用します。
制約を指定し、アルゴリズムを指定していない場合、ソルバーは自動的に
"interior-point"アルゴリズムに切り替わります。制約とアルゴリズムを指定する場合は、
"interior-point"アルゴリズムを指定する必要があります。
アルゴリズムの詳細については、制約付き最小二乗法に合わせて変更された fmincon アルゴリズムを参照してください。例については、制約付き非線形最小二乗の lsqnonlin と fmincon の比較を参照してください。
MATLAB コマンド
次の MATLAB コマンドに対応するリンクがクリックされました。
コマンドを MATLAB コマンド ウィンドウに入力して実行してください。Web ブラウザーは MATLAB コマンドをサポートしていません。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)