unmesh
エッジ行列を座標行列とラプラシアン行列に変換する
構文
[L,XY] = unmesh(E)
説明
[L,XY] = unmesh(E) は、M 行 4 列のエッジ行列 E について、ラプラシアン行列 L とメッシュの頂点の座標行列 XY を返します。エッジ行列の各行は、エッジの終点の座標 [x1 y1 x2 y2] を含まなければなりません。
入力引数
E | M 行 4 列のエッジ行列 E。 |
出力引数
L | グラフのラプラシアン行列表現。 |
XY | メッシュの頂点の座標行列。 |
例
簡単な例として、(1,1)、(1,–1)、(–1,–1)、および (–1,1) を頂点とする四角形があるとします。ここで、各頂点は四角形の 4 つのエッジでつながっており、(–1, –1) と (1,1) は対角線上でつながっています。
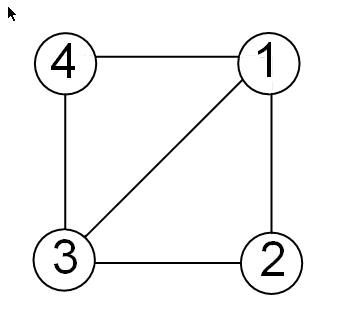
このグラフのエッジ行列 E は次のようになります。
E = [1 1 1 -1; % edge from 1 to 2 1 -1 -1 -1; % edge from 2 to 3 -1 -1 -1 1; % edge from 3 to 4 -1 -1 1 1; % edge from 3 to 1 -1 1 1 1] % edge from 4 to 1
unmesh を使用して、エッジ リストからラプラシアン行列とメッシュの座標行列を作成します。[L,XY] = unmesh(E);
unmesh は、ラプラシアン行列 L をスパース行列として返します。
L
L = (1,1) 3 (2,1) -1 (3,1) -1 (4,1) -1 (1,2) -1 (2,2) 2 (4,2) -1 (1,3) -1 (3,3) 2 (4,3) -1 (1,4) -1 (2,4) -1 (3,4) -1 (4,4) 3
L を表示するには、関数 full コマンドを使用します。full(L)
ans =
3 -1 -1 -1
-1 2 0 -1
-1 0 2 -1
-1 -1 -1 3
XY は、四角形の 4 隅の座標を返します。XY
XY =
-1 -1
-1 1
1 -1
1 1