erfinv
逆誤差関数
説明
例
値の逆誤差関数を求める
erfinv(0.25)
ans = 0.2253
入力が [-1,1] の範囲外の場合、erfinv は NaN を返します。erfinv は、-1 で -Inf、1 で Inf を返します。
erfinv([-2 -1 1 2])
ans = 1×4
NaN -Inf Inf NaN
行列の要素の逆誤差関数を求めます。
M = [0 -0.5; 0.9 -0.2]; erfinv(M)
ans = 2×2
0 -0.4769
1.1631 -0.1791
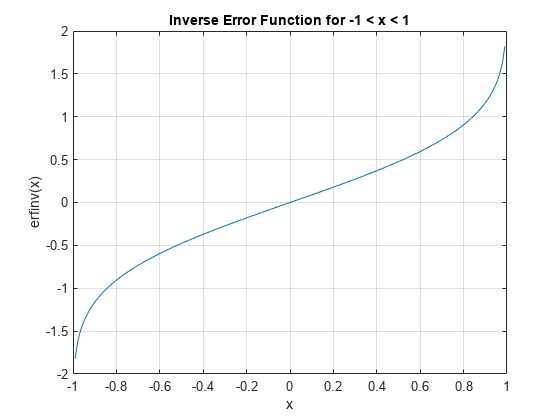
逆誤差関数のプロット
-1 < x < 1 について逆誤差関数をプロットします。
x = -1:0.01:1; y = erfinv(x); plot(x,y) grid on xlabel('x') ylabel('erfinv(x)') title('Inverse Error Function for -1 < x < 1')
ガウス分布乱数の生成
一様分布乱数を使用して、ガウス分布乱数を生成します。一様分布乱数 をガウス分布乱数 に変換するには、次の変換を使用します。
x は -1 + 2*rand(1,10000) の形式をとるので、erfinv の代わりに erfcinv を使用して精度を上げることができます。詳細については、ヒントを参照してください。
区間 [-1,1] に一様分布乱数を 10,000 個生成します。これらの乱数をガウス分布乱数に変換します。ヒストグラム プロットを使用して、乱数がガウス分布の形状に従うことを示します。
rng('default')
x = -1 + 2*rand(1,10000);
y = sqrt(2)*erfinv(x);
h = histogram(y);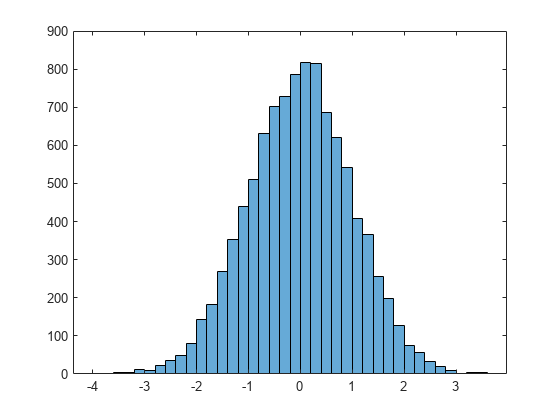
入力引数
x — 入力
実数 | 実数のベクトル | 実数の行列 | 実数の多次元配列
入力。実数、あるいは実数のベクトル、行列または多次元配列として指定します。x をスパースにすることはできません。
データ型: single | double
詳細
逆誤差関数
逆誤差関数 erfinv は、誤差関数の逆関数として定義され、次の式を満たします。
ヒント
erfinv(1-x)の形式の式では、代わりに逆相補誤差関数erfcinvを使用します。この置き換えでは精度が維持されます。xが1に近い場合、1 - xが小さい数値になり0に丸められることがあります。代わりに、erfinv(1-x)をerfcinv(x)に置き換えます。
拡張機能
tall 配列
メモリの許容量を超えるような多数の行を含む配列を計算します。
この関数は tall 配列を完全にサポートしています。詳細については、tall 配列を参照してください。
C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。
使用上の注意事項および制限事項:
厳密な単精度計算はサポートされていません。生成されたコードでは、単精度入力で単精度出力が生成されます。ただし、関数内の変数は倍精度である可能性があります。
スレッドベースの環境
MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。
この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。
GPU 配列
Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。
この関数は GPU 配列を完全にサポートしています。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
分散配列
Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。
この関数は分散配列を完全にサポートしています。詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
バージョン履歴
R2006a より前に導入
MATLAB コマンド
次の MATLAB コマンドに対応するリンクがクリックされました。
コマンドを MATLAB コマンド ウィンドウに入力して実行してください。Web ブラウザーは MATLAB コマンドをサポートしていません。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)