このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
線形方程式
計算上の考慮事項
技術計算の中で最も重要な問題の 1 つは、線形方程式を解くことです。
行列表記では一般的な問題は次のような形式になります。[2 つの行列 A と b があるとき、Ax= b または xA= b の条件のいずれかを満たす一意の行列 x は存在しますか。]
1 行 1 列の簡単な例を考えます。たとえば次の方程式について考えます。
7x = 21
上記に一意の解は存在しますか。
もちろん存在します。この方程式には一意の解 x = 3 が存在します。解は除算から簡単に得られます。
x = 21/7 = 3
解を求める場合、7 の逆数すなわち 7-1 = 0.142857... を計算し、この 7-1 に 21 を乗算する方法は通常 "使いません"。この方法では余計な計算ステップが必要となり、7-1 を有限小数値で表すと精度が低くなります。複数の未知数がある線形方程式にも同様の考え方で、MATLAB® は逆行列を使わずにこのような方程式を解きます。
標準の数学的な表記ではありませんが、MATLAB ではスカラーの場合と同じ除算記号を使用して一般的な連立方程式の解を記述します。2 つの除算記号 "スラッシュ" (/) および "バックスラッシュ" (\) が 2 つの MATLAB 関数 mrdivide および mldivide に対応します。これらの演算子は、係数行列の左右どちらかが未知の行列となる 2 つの状況で使用されます。
|
|
|
|
Ax = b または xA = b の方程式の両辺を A で割ると考えます。係数行列 A は常に「分母」 になります。
x = A\b に対する次元の整合性の条件は、2 つの行列 A と b の行数が同じであることです。その結果、解 x は b と同じ列数になり、行数は A の列数と同じになります。x = b/A に対しては、行と列の処理が反転します。
実際には Ax = b の形式の線形方程式の方が xA = b の形式より頻繁に使用されます。そのためバックスラッシュはスラッシュよりも頻繁に使用されます。この節の以降ではバックスラッシュ演算子を中心に説明します。スラッシュ演算子の特性は次の等式から推定できます。
(b/A)' = (A'\b').
係数行列 A は正方である必要はありません。A のサイズが m 行 n 列である場合、次の 3 つのケースがあります。
m = n | 正方システム。厳密解が得られます。 |
m > n | 未知数より方程式が多い過決定システム。最小二乗解を求めます。 |
m < n | 未知数より方程式が少ない劣決定システム。最大で m 個のゼロでない構成要素をもつ基本解を求めます。 |
mldivide アルゴリズム
mldivide 演算子は、さまざまなソルバーを使って各種の係数行列を処理します。実行するアルゴリズムは係数行列を調べて自動的に決められます。詳細については、関数 mldivide のリファレンス ページの「アルゴリズム」の節を参照してください。
一般解
線形方程式系 Ax = b の一般解は、すべての解を示します。次のようにして一般解を求めることができます。
対応する同次方程式 Ax = 0 を解きます。
nullコマンドを使用して「null(A)」と入力します。これによって、Ax = 0 の解空間の基底が返されます。どの解も基底ベクトルの線形結合になります。非同次方程式 Ax = b の特殊解を導出します。
Ax= b の解はすべて、手順 2 の Ax =b の特殊解に手順 1 の基底ベクトルの線形結合を加えたものとして表現できます。
この節の以降では、MATLAB を使用して手順 2 の Ax = b の特殊解を導出する方法を説明します。
正方システム
一般的な例は、正方係数行列 A と右辺に単一の列ベクトル b がある場合です。
特異でない係数行列
行列 A が特異でない場合、x = A\b の解は b と同じサイズになります。以下に例を示します。
A = pascal(3);
u = [3; 1; 4];
x = A\u
x =
10
-12
5A*x が u と等価であることを確認してください。
A と b が正方で同じサイズの場合、x= A\b も同じサイズになります。
b = magic(3);
X = A\b
X =
19 -3 -1
-17 4 13
6 0 -6A*x が b と等価であることを確認してください。
上記 2 つの例は、厳密に整数の解になります。これは係数行列がフル ランク行列 (特異でない) の pascal(3) であるためです。
特異な係数行列
正方行列 A が線形に独立した列をもっていない場合を「特異」といいます。A が特異な場合、Ax = b の解は存在しないかまたは一意ではありません。バックスラッシュ演算 A\b は、A が特異に近い場合か、厳密な特異性が検出された場合に警告を発します。
A が特異で Ax = b が解をもつ場合は、次のように入力することで一意ではない特殊解を導出できます。
P = pinv(A)*b
pinv(A) は A の疑似逆行列です。Ax = b が厳密解をもたない場合、pinv(A) は最小二乗解を返します。
以下に例を示します。
A = [ 1 3 7
-1 4 4
1 10 18 ]が特異であることは以下のように入力することでわかります。
rank(A)
ans =
2A はフル ランクではないため、いくつかの特異値がゼロに等しくなります。
厳密解。b =[5;2;12] に対して、方程式 Ax = b は次のような厳密解をもちます。
pinv(A)*b
ans =
0.3850
-0.1103
0.7066以下のように入力すると、pinv(A)*b が厳密解であることを確かめることができます。
A*pinv(A)*b
ans =
5.0000
2.0000
12.0000最小二乗解。ただし、b = [3;6;0] の場合、Ax = b は厳密解をもちません。この例の場合、pinv(A)*b は最小二乗解を返します。以下のように入力すると、
A*pinv(A)*b
ans =
-1.0000
4.0000
2.0000元のベクトル b には戻りません。
Ax = b が厳密解をもつかどうかは、拡大行列 [A b] を行の階段型に変換することによって判定できます。例では以下のようになります。
rref([A b])
ans =
1.0000 0 2.2857 0
0 1.0000 1.5714 0
0 0 0 1.0000最終行は最後の要素以外はすべてゼロであるため、方程式は解をもちません。この例の場合、pinv(A) は最小二乗解を返します。
過決定システム
この例では、実験データでのさまざまな曲線近似において過決定システムが頻繁に発生することを説明します。
量 y は、時間 t のいくつかの異なる値で測定され、次の観測値を生成します。次のステートメントで、データを入力して table 内に表示できます。
t = [0 .3 .8 1.1 1.6 2.3]'; y = [.82 .72 .63 .60 .55 .50]'; B = table(t,y)
B=6×2 table
t y
___ ____
0 0.82
0.3 0.72
0.8 0.63
1.1 0.6
1.6 0.55
2.3 0.5
減衰指数関数を使用してデータのモデル化を試します。
.
上記の式は、ベクトル y が他の 2 つのベクトルの線形結合で近似されることを示しています。一方はすべて 1 の定数ベクトルであり、もう一方は成分 exp(-t) を含むベクトルです。未知の係数 および は、モデルのデータの偏差の二乗和を最小化する最小二乗近似を実行することで計算可能です。2 つの未知数に対し 6 つの方程式があり、6 行 2 列の行列で表されます。
E = [ones(size(t)) exp(-t)]
E = 6×2
1.0000 1.0000
1.0000 0.7408
1.0000 0.4493
1.0000 0.3329
1.0000 0.2019
1.0000 0.1003
最小二乗解を求めるには、バックスラッシュ演算子を使用します。
c = E\y
c = 2×1
0.4760
0.3413
つまり、データの最小二乗近似は次のようになります。
次のステートメントでは、t を等間隔にインクリメントしてモデルを評価し、結果を元のデータとともにプロットします。
T = (0:0.1:2.5)'; Y = [ones(size(T)) exp(-T)]*c; plot(T,Y,'-',t,y,'o')
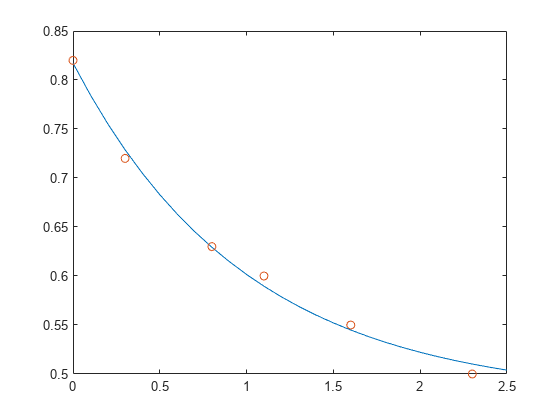
E*c は y と完全に等しくはありませんが、その差は元のデータの測定誤差より小さくなっている可能性があります。
方形行列 A は、線形独立の列がない場合はランク落ちとなります。A がランク落ちの場合、AX = B の最小二乗解は一意ではありません。A\B は A がランク落ちであり、最小二乗解を生成する場合に警告を発します。lsqminnorm を使用して、すべての解の中で最小のノルムをもつ解 X を求めることができます。
劣決定システム
この例では、劣決定システムの解が一意にならない理由について説明します。劣決定の線形システムは方程式より未知数の数が多くなります。MATLAB の行列の左除算演算で基底最小二乗解を求めます。つまり、m 行 n 列の係数行列には、最大 m 個の非ゼロの成分があります。
ここでは小さな乱数の例をあげます。
R = [6 8 7 3; 3 5 4 1] rng(0); b = randi(8,2,1)
R =
6 8 7 3
3 5 4 1
b =
7
8 線形システム Rp = b には、4 つの未知数の中に 2 つの式があります。この係数行列に含まれる整数は小さいため、format コマンドを使用して有理数形式の解を表示するのが適切です。特殊解は次のステートメントで得られます。
format rat
p = R\b
p =
0
17/7
0
-29/7 R(:,2) は R の最大ノルムをもつ列であるため、ゼロ以外の要素の 1 つは p(2) になります。R(:,2) を取り除くと R(:,4) が最大ノルムをもつため、他のゼロ以外の要素は p(4) になります。
劣決定システムの完全な一般解は、ヌル空間ベクトルの任意の線形結合に p を付加することで特性化され、有理数で表示するオプションにより関数 null を使用して求められます。
Z = null(R,'r')
Z =
-1/2 -7/6
-1/2 1/2
1 0
0 1 R*Z がゼロになります。残差 R*x - b は、以下に示す任意のベクトル x の場合は小さくなります。
x = p + Z*q
Z の列はヌル空間ベクトルであるため、積 Z*q はこれらのベクトルの線形結合です。
説明のため、任意の q を選択し、x を作成します。
q = [-2; 1]; x = p + Z*q;
残差のノルムを計算します。
format short
norm(R*x - b)ans = 2.6645e-15
解を無限に利用できる場合、最小ノルムをもつ解が特に重要となります。lsqminnorm を使用して最小ノルムをもつ最小二乗解を計算することができます。この解は norm(p) に対する可能な最小値をもちます。
p = lsqminnorm(R,b)
p =
-207/137
365/137
79/137
-424/137 複数の右辺の解法
同一の係数行列 A をもつが、異なる右辺 b をもつ線形システムを解く問題もあります。b の異なる値が同時に使用できる場合は、b を複数の列をもつ行列として構成し、単一のバックスラッシュ コマンドを使用して X = A\[b1 b2 b3 …] のように方程式系全体を一度に解くことができます。
ただし、b の異なる値がすべて同時に使用できない場合は、いくつかの方程式系を連続して解かなくてはなりません。これらの方程式系のいずれかをスラッシュ (/) またはバックスラッシュ (\) を使用して解く場合、演算子は係数行列 A を因数分解し、この行列の分解を使用して解を計算します。ただし、異なる b をもつ類似の方程式系を連続して解く場合、演算子は毎回同じ A の分解を演算するため冗長演算となります。
この問題を解決するには、A の分解を事前計算してから、その因子を再利用して異なる b の値の解を求めます。しかし実際には、この方法で分解を事前に計算することは困難です。その理由は、問題を解決するためにどの分解 (LU、LDL、コレスキーなど) を計算するかだけでなく、因子をどのように乗算するかについても知る必要があるからです。たとえば、LU 分解では、元のシステム Ax = b を解くために次の 2 つの線形システムを解かなければなりません。
[L,U] = lu(A); x = U \ (L \ b);
代わりに、連続する複数の右辺をもつ線形システムを解くために推奨される方法は、decomposition オブジェクトを使用する方法です。これらのオブジェクトによって、行列分解の事前計算によるパフォーマンス上の利点を活用できます。それらに、行列分解の使用方法に関する知識は必要 "ありません"。前述の LU 分解を以下のように置き換えることができます。
dA = decomposition(A,'lu');
x = dA\b;どの分解を使用すればよいかわからない場合は、decomposition(A) によりバックスラッシュと同様に A のプロパティに基づいて正しいタイプを選択します。
この方法によるパフォーマンス上の利点を測定する簡単なテストを次に示します。このテストでは、バックスラッシュ (\) と decomposition の両方を使用して、同じスパース線形システムの解決を 100 回繰り返します。
n = 1e3; A = sprand(n,n,0.2) + speye(n); b = ones(n,1); % Backslash solution tic for k = 1:100 x = A\b; end toc
Elapsed time is 9.006156 seconds.
% decomposition solution tic dA = decomposition(A); for k = 1:100 x = dA\b; end toc
Elapsed time is 0.374347 seconds.
この問題では、decomposition を使用した方法がバックスラッシュのみを使用した方法に比べてはるかに高速ですが、構文はシンプルです。
反復法
係数行列 A が大規模でスパース性がある場合、分解する方法は一般に効果がありません。反復法は近似解を生成できます。MATLAB は大規模でスパース性のある行列を扱う、いくつかの反復法を用意しています。
マルチスレッド計算
MATLAB は多数の線形代数関数と要素ごとに計算する数値関数のマルチスレッド計算をサポートしています。これらの関数は自動的にマルチスレッドで実行されます。関数や式に対し、複数の CPU を使用して計算を高速化するにはさまざまな条件があります。
関数は同時実行可能な部分へ簡単に分割できる処理を実行します。この分割部分は各処理間で通信をほとんど行わずに実行されるものでなければなりません。すなわちシーケンシャルな処理がほとんどないものを扱います。
データを分割し、複数の実行スレッドを管理する時間を含めても同時実行する価値があるように、データ サイズは十分に大きいものを扱います。たとえば配列が数千個以上の要素を含む場合は、ほとんどの関数に対して高速化の効果があります。
処理がメモリに拘束されないものを扱います。すなわち処理時間の大部分がメモリのアクセス時間にならないものを扱います。一般的には、シンプルな処理より複雑な処理をする関数の方が、高速化の効果があります。
関数 inv、lscov、linsolve、mldivide はマルチスレッド計算を有効にすると、大規模な倍精度配列 (10,000 個以上の要素) に対する計算速度が大幅に上昇します。
参考
mldivide | mrdivide | pinv | decomposition | lsqminnorm
