多次元配列
MATLAB® の多次元配列は、2 より大きい次元をもつ配列です。行列において、2 次元は行と列で表されます。

各要素は、行インデックスと列インデックスの 2 つの添字で定義されます。多次元配列は 2 次元行列の拡張であり、インデックス付けに追加の添字を使用します。たとえば、3 次元配列は 3 つの添字を使います。最初の 2 つは行列と同様ですが、3 番目の次元は要素の "ページ" または "シート" を表します。
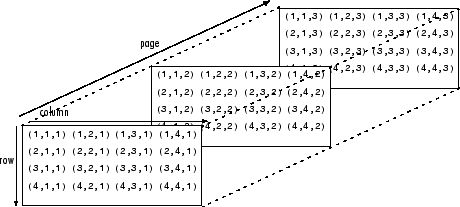
多次元配列の作成
最初に 2 次元配列を作成してから、それを拡張することで多次元配列を作成できます。たとえば、最初に 3 行 3 列の行列を 3 次元配列の最初のページとして定義します。
A = [1 2 3; 4 5 6; 7 8 9]
A = 3×3
1 2 3
4 5 6
7 8 9
今度は 2 ページ目を追加します。これを行うには、別の 3 行 3 列の行列を、3 番目の次元でインデックス値 2 に代入します。構文 A(:,:,2) は最初と 2 番目の次元でコロンを使用し、代入の右辺からすべての行と列を含めます。
A(:,:,2) = [10 11 12; 13 14 15; 16 17 18]
A =
A(:,:,1) =
1 2 3
4 5 6
7 8 9
A(:,:,2) =
10 11 12
13 14 15
16 17 18
関数 cat は多次元配列の作成に便利なツールです。たとえば、A を 3 ページ目と連結して新しい 3 次元配列 B を作成します。最初の引数は、どの次元に沿って連結されるのかを示します。
B = cat(3,A,[3 2 1; 0 9 8; 5 3 7])
B =
B(:,:,1) =
1 2 3
4 5 6
7 8 9
B(:,:,2) =
10 11 12
13 14 15
16 17 18
B(:,:,3) =
3 2 1
0 9 8
5 3 7
多次元配列をすばやく拡張する別の方法は、1 つの要素をページ全体に代入することです。たとえば、4 ページ目をすべての 0 が含まれる B に追加します。
B(:,:,4) = 0
B =
B(:,:,1) =
1 2 3
4 5 6
7 8 9
B(:,:,2) =
10 11 12
13 14 15
16 17 18
B(:,:,3) =
3 2 1
0 9 8
5 3 7
B(:,:,4) =
0 0 0
0 0 0
0 0 0
要素へのアクセス
多次元配列の要素にアクセスするには、ベクトルおよび行列と同様に整数の添字を使用します。たとえば、A の最初の行、2 番目の列、2 ページ目である A の 1,2,2 要素を見つけます。
A
A =
A(:,:,1) =
1 2 3
4 5 6
7 8 9
A(:,:,2) =
10 11 12
13 14 15
16 17 18
elA = A(1,2,2)
elA = 11
2 番目の次元でインデックス ベクトル [1 3] を使用し、A の各ページの最初と最後の列にのみアクセスします。
C = A(:,[1 3],:)
C =
C(:,:,1) =
1 3
4 6
7 9
C(:,:,2) =
10 12
13 15
16 18
各ページの最初と 3 番目の行を見つけるには、コロン演算子を使用してインデックス ベクトルを作成します。
D = A(2:3,:,:)
D =
D(:,:,1) =
4 5 6
7 8 9
D(:,:,2) =
13 14 15
16 17 18
配列の操作
多次元配列の要素は、ベクトルおよび行列と同様にさまざまな方法で移動できます。reshape、permute、squeeze は要素を再配列するのに便利な関数です。2 ページをもつ 3 次元配列を考えます。
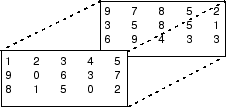
多次元配列の形状変更は、特定の操作の実行またはデータの可視化に便利です。関数 reshape を使用して 3 次元配列の要素を 6 行 5 列の行列に再配列します。
A = [1 2 3 4 5; 9 0 6 3 7; 8 1 5 0 2]; A(:,:,2) = [9 7 8 5 2; 3 5 8 5 1; 6 9 4 3 3]; B = reshape(A,[6 5])
B = 6×5
1 3 5 7 5
9 6 7 5 5
8 5 2 9 3
2 4 9 8 2
0 3 3 8 1
1 0 6 4 3
reshape は列単位で操作し、最初のページから開始して 2 ページ目に移動し、A の各列から連続する要素を取ることで新しい行列を作成します。
置換は、配列の次元の順序を再配列するために使用されます。3 次元配列 M を考えます。
M(:,:,1) = [1 2 3; 4 5 6; 7 8 9]; M(:,:,2) = [0 5 4; 2 7 6; 9 3 1]
M =
M(:,:,1) =
1 2 3
4 5 6
7 8 9
M(:,:,2) =
0 5 4
2 7 6
9 3 1
関数 permute を使用して、2 番目の引数で次元の順序を指定し、各ページで行と列の添字を交換します。今度は M の元の行が列になり、列が行になります。
P1 = permute(M,[2 1 3])
P1 =
P1(:,:,1) =
1 4 7
2 5 8
3 6 9
P1(:,:,2) =
0 2 9
5 7 3
4 6 1
同様に、M の行とページの添字を交換します。
P2 = permute(M,[3 2 1])
P2 =
P2(:,:,1) =
1 2 3
0 5 4
P2(:,:,2) =
4 5 6
2 7 6
P2(:,:,3) =
7 8 9
9 3 1
多次元配列を操作する場合、長さ 1 の不要な次元をもつものが発生する可能性があります。関数 squeeze は、長さ 1 の次元を排除する別のタイプの操作を実行します。たとえば、関数 repmat を使用して、要素がそれぞれ 5 で、3 番目の次元が長さ 1 である 2 x 3 x 1 x 4 の配列を作成します。
A = repmat(5,[2 3 1 4])
A =
A(:,:,1,1) =
5 5 5
5 5 5
A(:,:,1,2) =
5 5 5
5 5 5
A(:,:,1,3) =
5 5 5
5 5 5
A(:,:,1,4) =
5 5 5
5 5 5
szA = size(A)
szA = 1×4
2 3 1 4
numdimsA = ndims(A)
numdimsA = 4
関数 squeeze を使用して 3 番目の次元を削除し、3 次元配列にします。
B = squeeze(A)
B =
B(:,:,1) =
5 5 5
5 5 5
B(:,:,2) =
5 5 5
5 5 5
B(:,:,3) =
5 5 5
5 5 5
B(:,:,4) =
5 5 5
5 5 5
szB = size(B)
szB = 1×3
2 3 4
numdimsB = ndims(B)
numdimsB = 3