このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
bwdist
バイナリ イメージの距離変換
説明
例
入力引数
出力引数
ヒント
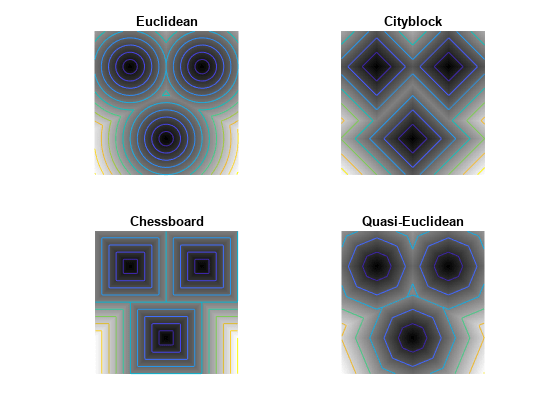
bwdistは、特に 2 次元の場合、高速アルゴリズムを使用して真のユークリッド距離変換を計算します。他のメソッドは、主に教育を目的としたものです。ただし、別の距離変換には、多次元入力イメージ、特に多数の非ゼロ要素をもつものに対しては、極めて高速なものもあります。関数
bwdistは Version 6.4 (R2009b) で変更されました。以前のバージョンの Image Processing Toolbox では、ユークリッド距離変換やそれに関連したラベル行列の計算に、さまざまなアルゴリズムが使用されていました。以前の実装時と同じ結果を得る必要がある場合、関数bwdist_oldを使用してください。
アルゴリズム
参照
[1] Maurer, Calvin, Rensheng Qi, and Vijay Raghavan, "A Linear Time Algorithm for Computing Exact Euclidean Distance Transforms of Binary Images in Arbitrary Dimensions," IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 25, No. 2, February 2003, pp. 265-270.
[2] Rosenfeld, Azriel and John Pfaltz, "Sequential operations in digital picture processing," Journal of the Association for Computing Machinery, Vol. 13, No. 4, 1966, pp. 471-494.
[3] Paglieroni, David, "Distance Transforms: Properties and Machine Vision Applications," Computer Vision, Graphics, and Image Processing: Graphical Models and Image Processing, Vol. 54, No. 1, January 1992, pp. 57-58.