スライディングウィンドウ法と指数の重み付け法

moving オブジェクトと moving ブロックは、スライディングウィンドウ法と指数の重み付け法のいずれかまたは両方を使用して、ストリーミング信号の移動統計を計算します。スライディングウィンドウ法は有限インパルス応答になります。一方、指数の重み付け法は無限インパルス応答になります。データの有限区間の統計量を解析するには、スライディングウィンドウ法を使用します。指数の重み付け法は係数が少なくて済むため、組み込みアプリケーションにより適しています。

オブジェクト、ブロック	スライディングウィンドウ法	指数の重み付け法
`dsp.MedianFilter`, Median Filter	✓
`dsp.MovingAverage`, Moving Average	✓	✓
`dsp.MovingMaximum`, Moving Maximum	✓
`dsp.MovingMinimum`, Moving Minimum	✓
`dsp.MovingRMS`, Moving RMS	✓	✓
`dsp.MovingStandardDeviation`, Moving Standard Deviation	✓	✓
`dsp.MovingVariance`, Moving Variance	✓	✓
`powermeter`, Power Meter	✓

スライディングウィンドウ法

スライディングウィンドウ法では、データ上で指定の長さ Len のウィンドウをサンプルごとに移動させ、ウィンドウ内のデータの統計量を計算します。各入力サンプルの出力は、現在のサンプルと以前の Len - 1 個のサンプルから成るウィンドウ内の統計量になります。最初の出力サンプルを計算するために、アルゴリズムはホップサイズの数の入力サンプルを受け取るまで待機します。ホップサイズは、ウィンドウの長さからオーバーラップの長さを引いた値として定義されます。ウィンドウ内の残りのサンプルはゼロと見なされます。たとえば、ウィンドウの長さが 5 でオーバーラップの長さが 2 の場合、アルゴリズムは最初の出力サンプルを計算するために、入力サンプルを 3 つ受け取るまで待機します。最初の出力の生成後、ホップサイズの数の入力サンプルごとに後続の出力サンプルを生成します。移動統計アルゴリズムは、状態をもち、前のデータを記憶します。

Moving Maximum、Moving Minimum、および Median Filter のオブジェクトとブロックの場合、オーバーラップの長さは指定できません。アルゴリズムは、オーバーラップの長さをウィンドウの長さから 1 を引いた値と仮定します。

スライディングウィンドウ法を使用してストリーミング入力データの移動平均を計算する例を考えます。アルゴリズムはウィンドウの長さ 4 とオーバーラップの長さ 3 を使用します。受け取った各入力サンプルで、長さ 4 のウィンドウがデータに沿って移動します。

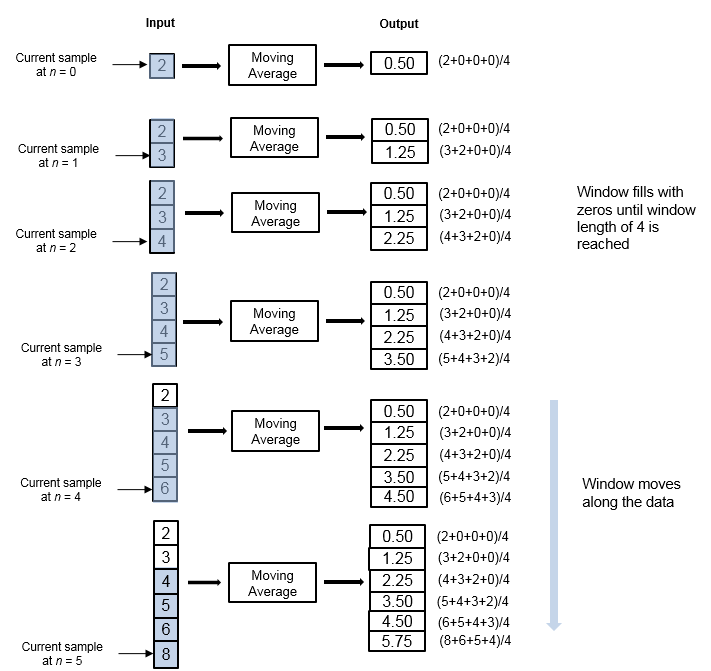
このウィンドウは長さが有限であるため、このアルゴリズムは有限インパルス応答フィルターとなります。データの有限区間の統計量を解析するには、スライディングウィンドウ法を使用します。

ウィンドウの長さの効果

ウィンドウの長さは、アルゴリズムが統計量の計算に使用するデータの長さを定義します。新しいデータが入ると、ウィンドウが移動します。ウィンドウが大きければ、計算された統計量はデータの定常統計量に近くなります。急速に変化しないデータの場合は、長いウィンドウを使用することで滑らかな統計量が得られます。急速に変化するデータの場合は、小さいウィンドウを使用します。

オーバーラップの長さの効果

[オーバーラップの長さ] パラメーターがウィンドウの長さから 1 を引いた値よりも小さい値に設定されている場合、アルゴリズムは出力をホップサイズ (ウィンドウの長さからオーバーラップの長さを引いた値) の分だけダウンサンプリングします。上の例では、オーバーラップの長さは 1 に設定されています。この場合、アルゴリズムは n = 3 で始まる 3 番目の入力サンプルごとに 1 つの出力サンプルを生成します。

指数の重み付け法

指数の重み付け法は無限インパルス応答になります。このアルゴリズムでは、一連の重みが計算され、その重みがデータサンプルに再帰的に適用されます。データが古くなるほど、重み係数の大きさは指数的に小さくなります (0 になることはありません)。つまり、現在のサンプルの統計量に対する影響は、古いデータよりも新しいデータの方が大きくなります。このアルゴリズムの応答は無限インパルス応答であるため、係数が少なくて済み、組み込みアプリケーションにより適しています。

重み係数の変化率は忘却係数の値で決まります。忘却係数 0.1 よりも忘却係数 0.9 の方が古いデータに対する重みが大きくなります。新しいデータにより大きな重みを与えるには、忘却係数を 0 に近づけます。急速に変化するデータの小さなシフトを検出する場合は、小さな値 (0.5 未満) のほうがより適しています。忘却係数が 1.0 の場合は無限に記憶します。以前のサンプルに対する重みはすべて同じになります。忘却係数の最適値は、データストリームによって異なります。与えられたデータストリームの忘却係数の最適値を計算する方法については、[1]を参照してください。

指数の重み付け法を使用して移動平均を計算する例を考えます。忘却係数は 0.9 です。

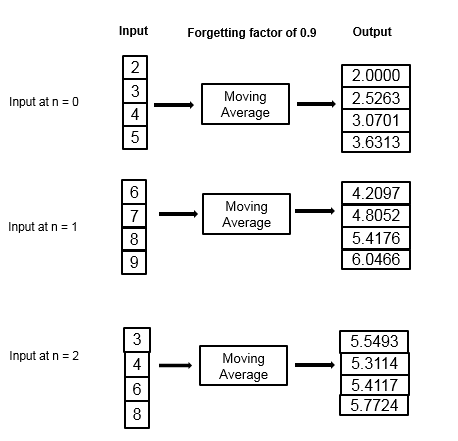
移動平均アルゴリズムでは、受け取った各データサンプルについて、次の再帰方程式を使用して重みの更新と移動平均の計算が再帰的に行われます。

$\begin{array}{l} w_{N, λ} = λ w_{N - 1, λ} + 1 \\ {\bar{x}}_{N, λ} = (1 - \frac{1}{w_{N, λ}}) {\bar{x}}_{N - 1, λ} + (\frac{1}{w_{N, λ}}) x_{N} \end{array}$

λ — 忘却係数。
$w_{N, λ}$ — 現在のデータサンプルに適用される重み係数。
$x_{N}$ — 現在のデータ入力サンプル。
${\bar{x}}_{N - 1, λ}$ — 前のサンプルの移動平均。
$(1 - \frac{1}{w_{N, λ}}) {\bar{x}}_{N - 1, λ}$ — 平均に対する前のデータの影響。
${\bar{x}}_{N, λ}$ — 現在のサンプルの移動平均。

データ	重み $w_{N, λ} = λ w_{N - 1, λ} + 1$	平均値 ${\bar{x}}_{N, λ} = (1 - \frac{1}{w_{N, λ}}) {\bar{x}}_{N - 1, λ} + (\frac{1}{w_{N, λ}}) x_{N}$
フレーム 1
2	1.N = 1 の場合、この値は 1 になります。	2
3	0.9×1+1 = 1.9	(1–(1/1.9))×2+(1/1.9)×3 = 2.5263
4	0.9×1.9+1 = 2.71	(1–(1/2.71))×2.52+(1/2.71)×4 = 3.0701
5	0.9×2.71+1 = 3.439	(1–(1/3.439))×3.07+(1/3.439)×5 = 3.6313
フレーム 2
6	0.9×3.439+1 = 4.095	(1–(1/4.095))×3.6313+(1/4.095)×6 = 4.2097
7	0.9×4.095+1 = 4.6855	(1–(1/4.6855))×4.2097+(1/4.6855)×7 = 4.8052
8	0.9×4.6855+1 = 5.217	(1–(1/5.217))×4.8052+(1/5.217)×8 = 5.4176
9	0.9×5.217+1 = 5.6953	(1–(1/5.6953))×5.4176+(1/5.6953)×9 = 6.0466
フレーム 3
3	0.9×5.6953+1 = 6.1258	(1–(1/6.1258))×6.0466+(1/6.1258)×3 = 5.5493
4	0.9×6.1258+1 = 6.5132	(1–(1/6.5132))×5.5493+(1/6.5132)×4 = 5.3114
6	0.9×6.5132+1 = 6.8619	(1–(1/6.8619))×5.3114+(1/6.8619)×6 = 5.4117
8	0.9×6.8619+1 = 7.1751	(1–(1/7.1751))×5.4117+(1/7.1751)×8 = 5.7724

移動平均アルゴリズムは、状態をもち、前のタイムステップのデータを記憶します。

最初のサンプルでは、N = 1 の場合、アルゴリズムによって $w_{N, λ}$ = 1 が選択されます。次のサンプルでは、重み係数が更新され、再帰方程式を使用して平均値が計算されます。

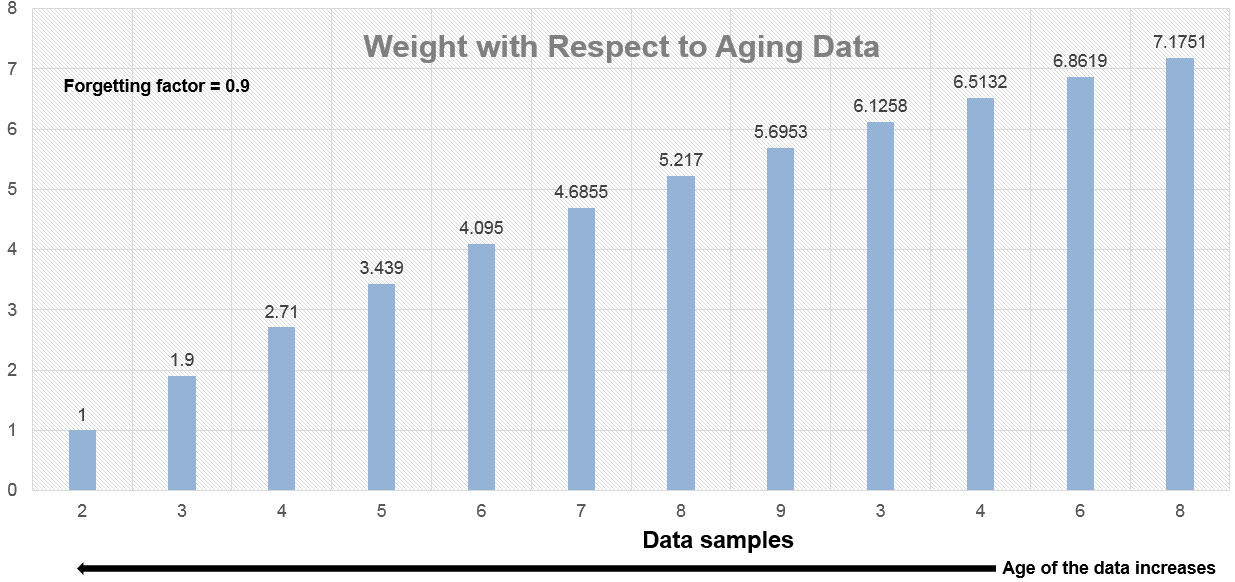
データが古くなるほど、重み係数の大きさは指数的に小さくなります (0 になることはありません)。つまり、現在の平均に対する影響は古いデータよりも新しいデータの方が大きくなります。

忘却係数が 0.5 の場合、忘却係数が 0.9 の場合と比べ、古いデータに適用される重みは小さくなります。

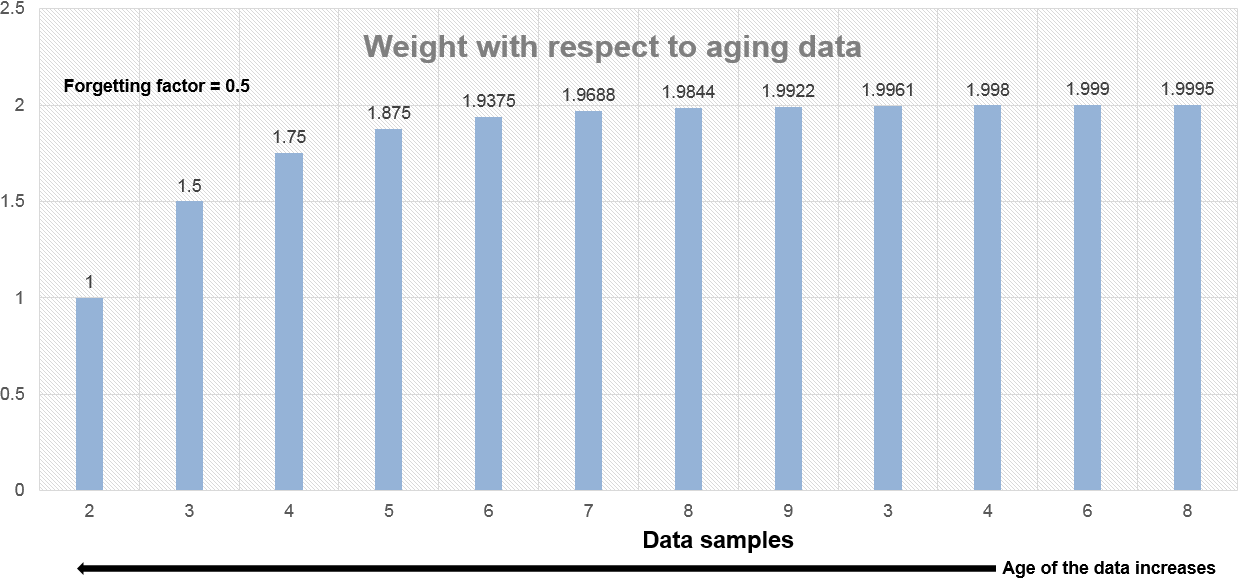
忘却係数が 1 の場合、すべてのデータサンプルに同じ重みが適用されます。この場合、指数の重み付け法は、ウィンドウの長さが無限大であるスライディングウィンドウ法と同じになります。

信号が急速に変化する場合は、小さな忘却係数を使用します。忘却係数が小さい場合、過去のデータが現在の平均値に与える効果は小さくなります。これにより、過渡特性がより急峻になります。例として、変化が急速でノイズを含むステップ信号を考えます。

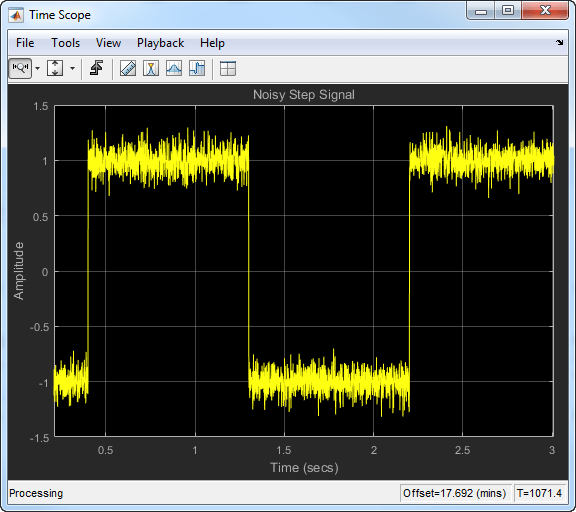
指数の重み付け法を使用して、この信号の移動平均を計算します。忘却係数が 0.8、0.9、0.99 の場合について、アルゴリズムのパフォーマンスを比較します。

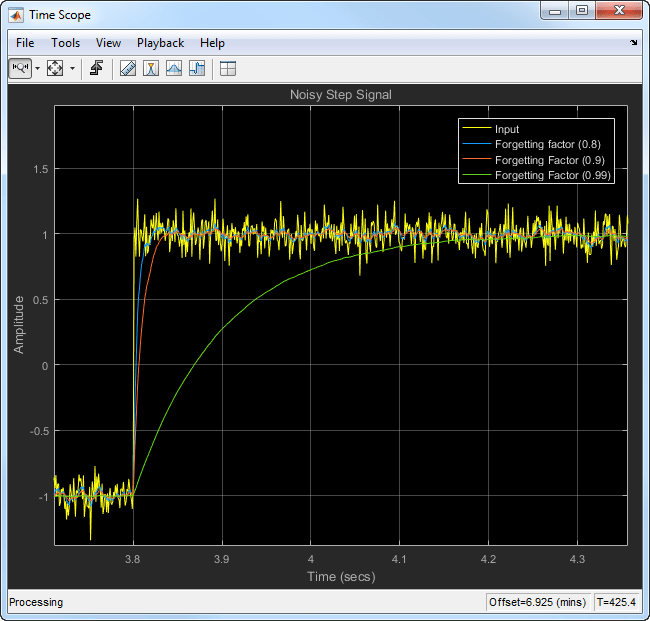
プロットをズームインすると、忘却係数が小さいときに移動平均の過渡特性が急峻であることがわかります。そのため、急速に変化するデータにより適しています。

移動平均アルゴリズムの詳細については、dsp.MovingAverage System object™ または Moving Average ブロックのページにあるアルゴリズムの節を参照してください。

その他の移動統計アルゴリズムの詳細については、System object および各ブロックのページにあるアルゴリズムの節を参照してください。

参照

[1] Bodenham, Dean. “Adaptive Filtering and Change Detection for Streaming Data.” PH.D. Thesis. Imperial College, London, 2012.