制御システムのむだ時間に対する感度
この例では、システムのむだ時間に対して閉ループ制御システムの感度を検証する方法を説明します。
むだ時間が正確に理解されていることはほとんどありません。したがって、制御システムが遅延の値に対し、どれほどの感度があるかを理解することが重要な場合が多くあります。そのような感度解析は、LTI 配列と InternalDelay プロパティを使用して簡単に実行できます。たとえば、「遅延をもつ制御システムの解析」の例の「デッド タイムをもつ PI 制御ループ」で作成されるノッチ フィルター付き PI 制御システムについて考えます。次のコマンドにより、そのような閉ループ システムの LTI モデルとなる、入力遅延、PI コントローラーおよびノッチ フィルターをもつ 3 次のプラントを作成します。
s = tf('s');
G = exp(-2.6*s)*(s+3)/(s^2+0.3*s+1);
C = 0.06 * (1 + 1/s);
T = feedback(ss(G*C),1);
notch = tf([1 0.2 1],[1 .8 1]);
C = 0.05 * (1 + 1/s);
Tnotch = feedback(ss(G*C*notch),1);閉ループ システム Tnotch の内部遅延を検証します。
Tnotch.InternalDelay
ans = 2.6000
プラント G の 2.6 秒の入力遅延は、閉ループ システムの 2.6 秒の内部遅延になります。この遅延の変動に対する Tnotch の応答の感度を検証するために、Tnotch のコピーの配列を作成します。そこで、配列内で内部遅延を変動させます。
Tsens = repsys(Tnotch,[1 1 5]); tau = linspace(2,3,5); for j = 1:5; Tsens(:,:,j).InternalDelay = tau(j); end
配列 Tsens には、2.0 ~ 3.0 の範囲の内部遅延をもつ 5 つのモデルが含まれます。
これらのモデルのステップ応答を検証します。
stepplot(Tsens)
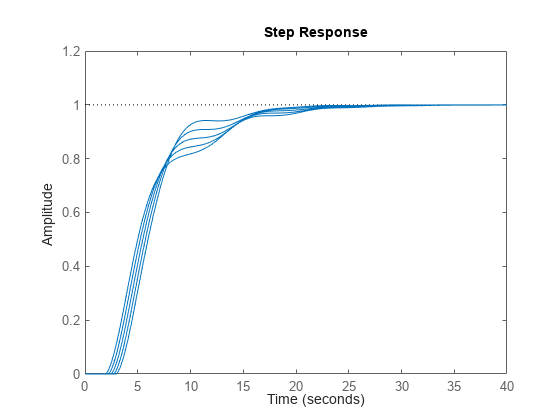
このプロットでは、遅延の値の不確かさは閉ループ特性への影響が小さいことを示しています。
