このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
MIMO システムの紹介
この例では、多入力多出力 (MIMO) システムを示します。このシステムでは、無線通信システムの送信端と受信端で複数のアンテナを使用します。MIMO システムは、複数のアンテナを使用することで潜在的なキャパシティ ゲインを得られるので、通信システムに広範囲に採用されています。複数のアンテナで、システムの帯域幅要件を変えることなく、時間次元と周波数次元以外に空間次元を使用します。
汎用の通信リンクについて、この例では従来の受信ダイバーシティではなく送信ダイバーシティに焦点を合わせます。フラット フェージング レイリー チャネルを使用して、直交空間時間ブロック符号化 (OSTBC) の概念について示します。これは、複数の送信アンテナを使用する場合に採用できます。ここでは、送信受信アンテナの複数の組の間で独立したフェージングがチャネルに発生すると仮定します。
選択した 1 つのシステムについては、受信側でチャネルを完全に把握している場合と不完全に推定したときの特性を比較し、その低下度の測定値も提示します。
パート 1: 送信ダイバーシティと受信ダイバーシティ
ダイバーシティ受信の使用は、通信リンク全体に及ぶフェージングの影響を緩和するための広く知られた手法の 1 つです。ただし、ほとんどの場合、受信端側で実施されます。[ 1 ] では、Alamouti が送信側で複数のアンテナを使用して同程度のダイバーシティ ゲインを得られる送信ダイバーシティ方式を提案しています。こちらの方がより実際的であると考えられました。たとえば、この方式なら複数のアンテナを設置する必要があるのは基地局だけであるのに対して、セルラー方式では移動体ごとに複数のアンテナが必要とされるためです。
この節では、フラット フェージング レイリー チャネル経由で同期 2 位相偏移変調 (BPSK) 変調をシミュレーションして、送信ダイバーシティと受信ダイバーシティの比較について示します。送信ダイバーシティでは 2 つの送信アンテナと 1 つの受信アンテナ (2x1 と表記) を使用し、受信ダイバーシティでは 1 つの送信アンテナと 2 つの受信アンテナ (1x2 と表記) を使用します。
シミュレーションでは、あるエンドツーエンド システムを対象とし、符号化または送信された信号、チャネル モデル、および受信信号の受信と復調について示します。また、比較のため、ダイバーシティのないリンク (送信と受信のアンテナが 1 つしかないケース)、および 2 次ダイバーシティ リンクの理論上の特性も提示します。ここでは、すべてのシステムについて受信側でチャネルが完全に把握されていると仮定します。Eb/No 点の範囲でシミュレーションを実行して、さまざまなシステムを比較できるようにする BER 結果を生成します。
一般のシミュレーションのパラメーターを定義することから始めます。
frmLen = 100; % frame length numPackets = 1000; % number of packets EbNo = 0:2:20; % Eb/No varying to 20 dB N = 2; % maximum number of Tx antennas M = 2; % maximum number of Rx antennas P = 2; % modulation order
次にシミュレーションをセットアップします。
% Create comm.OSTBCEncoder and comm.OSTBCCombiner System objects(TM) ostbcEnc = comm.OSTBCEncoder; ostbcComb = comm.OSTBCCombiner; % Convert Eb/No values to SNR values. The output of the BPSK modulator % generates unit power signals. SNR = convertSNR(EbNo,"ebno","BitsPerSymbol",1); % Create comm.ErrorRate calculator System objects to evaluate BER. errorCalc1 = comm.ErrorRate; errorCalc2 = comm.ErrorRate; errorCalc3 = comm.ErrorRate; % Since the AWGN function as well as the RANDI function use the default % random stream, the following commands are executed so that the results % will be repeatable, i.e., same results will be obtained for every run of % the example. The default stream will be restored at the end of the % example. s = rng(55408); % Pre-allocate variables for speed H = zeros(frmLen, N, M); ber_noDiver = zeros(3,length(EbNo)); ber_Alamouti = zeros(3,length(EbNo)); ber_MaxRatio = zeros(3,length(EbNo)); ber_thy2 = zeros(1,length(EbNo));
% Set up a figure for visualizing BER results fig = figure; grid on; ax = fig.CurrentAxes; hold(ax,'on'); ax.YScale = 'log'; xlim(ax,[EbNo(1), EbNo(end)]); ylim(ax,[1e-4 1]); xlabel(ax,'Eb/No (dB)'); ylabel(ax,'BER'); fig.NumberTitle = 'off'; fig.Renderer = 'zbuffer'; fig.Name = 'Transmit vs. Receive Diversity'; title(ax,'Transmit vs. Receive Diversity'); set(fig, 'DefaultLegendAutoUpdate', 'off'); fig.Position = figposition([15 50 25 30]); % Loop over several EbNo points for idx = 1:length(EbNo) reset(errorCalc1); reset(errorCalc2); reset(errorCalc3); % Loop over the number of packets for packetIdx = 1:numPackets % Generate data vector per frame data = randi([0 P-1], frmLen, 1); % Modulate data modData = pskmod(data,P); % Alamouti Space-Time Block Encoder encData = ostbcEnc(modData); % Create the Rayleigh distributed channel response matrix % for two transmit and two receive antennas H(1:N:end, :, :) = (randn(frmLen/2, N, M) + ... 1i*randn(frmLen/2, N, M))/sqrt(2); % assume held constant for 2 symbol periods H(2:N:end, :, :) = H(1:N:end, :, :); % Extract part of H to represent the 1x1, 2x1 and 1x2 channels H11 = H(:,1,1); H21 = H(:,:,1)/sqrt(2); H12 = squeeze(H(:,1,:)); % Pass through the channels chanOut11 = H11 .* modData; chanOut21 = sum(H21.* encData, 2); chanOut12 = H12 .* repmat(modData, 1, 2); % Add AWGN rxSig11 = awgn(chanOut11,SNR(idx)); rxSig21 = awgn(chanOut21,SNR(idx)); rxSig12 = awgn(chanOut12,SNR(idx)); % Alamouti Space-Time Block Combiner decData = ostbcComb(rxSig21, H21); % ML Detector (minimum Euclidean distance) demod11 = pskdemod(rxSig11.*conj(H11),P); demod21 = pskdemod(decData,P); demod12 = pskdemod(sum(rxSig12.*conj(H12), 2),P); % Calculate and update BER for current EbNo value % for uncoded 1x1 system ber_noDiver(:,idx) = errorCalc1(data, demod11); % for Alamouti coded 2x1 system ber_Alamouti(:,idx) = errorCalc2(data, demod21); % for Maximal-ratio combined 1x2 system ber_MaxRatio(:,idx) = errorCalc3(data, demod12); end % end of FOR loop for numPackets % Calculate theoretical second-order diversity BER for current EbNo ber_thy2(idx) = berfading(EbNo(idx), 'psk', 2, 2); % Plot results semilogy(ax,EbNo(1:idx), ber_noDiver(1,1:idx), 'r*', ... EbNo(1:idx), ber_Alamouti(1,1:idx), 'go', ... EbNo(1:idx), ber_MaxRatio(1,1:idx), 'bs', ... EbNo(1:idx), ber_thy2(1:idx), 'm'); legend(ax,'No Diversity (1Tx, 1Rx)', 'Alamouti (2Tx, 1Rx)',... 'Maximal-Ratio Combining (1Tx, 2Rx)', ... 'Theoretical 2nd-Order Diversity'); drawnow; end % end of for loop for EbNo % Perform curve fitting and replot the results fitBER11 = berfit(EbNo, ber_noDiver(1,:)); fitBER21 = berfit(EbNo, ber_Alamouti(1,:)); fitBER12 = berfit(EbNo, ber_MaxRatio(1,:)); semilogy(ax,EbNo, fitBER11, 'r', EbNo, fitBER21, 'g', EbNo, fitBER12, 'b'); hold(ax,'off'); % Restore default stream rng(s);
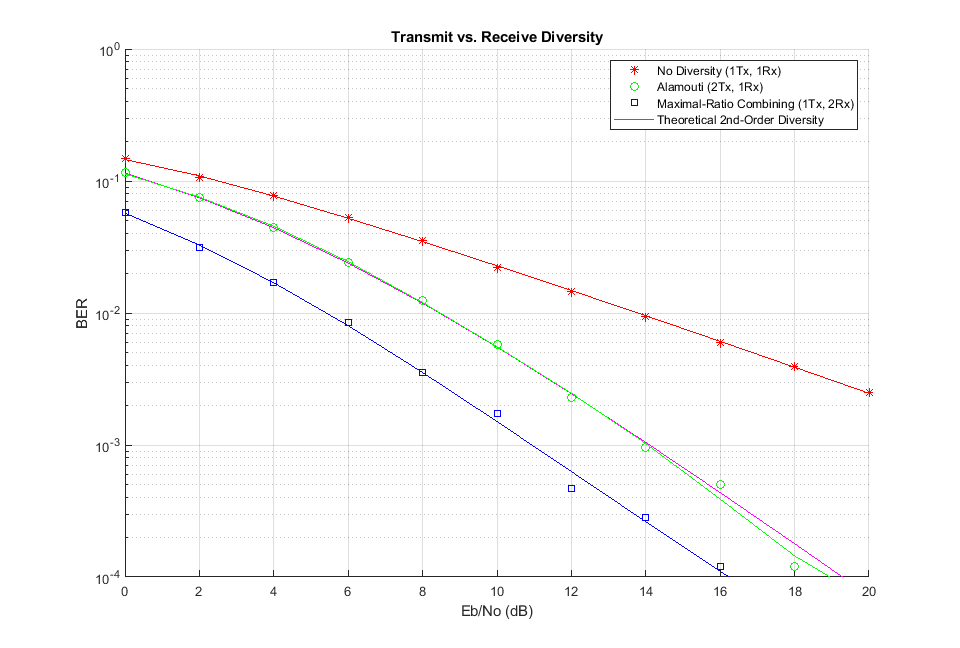
送信ダイバーシティ システムの計算の複雑度は、受信ダイバーシティ システムの場合と非常によく似ています。
シミュレーションの結果により、2 つの送信アンテナと 1 つの受信アンテナを使用する場合のダイバーシティ次数は、1 つの送信アンテナと 2 つの受信アンテナを使用する最大比率の組み合わせ (MRC) システムと同じであることがわかります。
また、MRC 受信ダイバーシティと比較して送信ダイバーシティには 3 dB のマイナスがあることも認められます。こうなるのは、総送信電力がどちらのケースでも同じになるようにモデル化したためです。これら 2 つのケースの受信電力が同じになるように送信電力を較正すると、特性は同じになります。2 次ダイバーシティ リンクの理論上の特性は、送信ダイバーシティ システムに一致します。これは、すべてのダイバーシティ分枝で総電力が正規化されるからです。
付属の関数スクリプト mrc1m.m と ostbc2m.m は、関心のあるユーザーがさらに調べるうえで役立ちます。
パート 2: チャネル推定付き時空間ブロック符号化
直交デザイン理論に基づき、Tarokh らは [ 2] Alamouti の送信ダイバーシティ方式を任意本数の送信アンテナに一般化し、空間時間ブロック符号化の概念に到達しました。複素数信号コンスタレーションについて、Alamouti の方式が 2 つの送信アンテナに対する唯一のフルレート方式であることを示しました。
この節では、2 つの受信アンテナがあるそのような方式 (2x2 システムなど) の特性について、チャネル推定がある場合とない場合に分けて検討します。受信側がチャネル状態情報を把握していない現実的なシナリオでは、特性を受信信号から抽出しなければなりません。チャネル推定器が、各パケットの先頭に追加される直交パイロット信号を使用して抽出を実行するものと仮定します [ 3 ]。また、パケットの長さの間、チャネルは変わらない (つまり、低速フェージングが発生する) と仮定します。
前の節で説明したのと同じシミュレーションをここでも使用します。したがって、2 つの送信アンテナと 2 つの受信アンテナを使用する空間時間ブロック符号化されたシステムの BER 性能を推定できます。
今回も、最初に共通なシミュレーション パラメーターを定義します。
frmLen = 100; % frame length maxNumErrs = 300; % maximum number of errors maxNumPackets = 3000; % maximum number of packets EbNo = 0:2:12; % Eb/No varying to 12 dB N = 2; % number of Tx antennas M = 2; % number of Rx antennas pLen = 8; % number of pilot symbols per frame W = hadamard(pLen); pilots = W(:, 1:N); % orthogonal set per transmit antenna
次にシミュレーションをセットアップします。
% Create a comm.MIMOChannel System object to simulate the 2x2 spatially % independent flat-fading Rayleigh channel chan = comm.MIMOChannel( ... 'MaximumDopplerShift', 0, ... 'SpatialCorrelationSpecification', 'None', ... 'NumTransmitAntennas', N, ... 'NumReceiveAntennas', M, ... 'PathGainsOutputPort', true); % Change the NumReceiveAntennas property value of the hAlamoutiDec System % object to M that is 2 release(ostbcComb); ostbcComb.NumReceiveAntennas = M; % Set the global random stream for repeatability s = rng(55408); % Pre-allocate variables for speed HEst = zeros(frmLen, N, M); ber_Estimate = zeros(3,length(EbNo)); ber_Known = zeros(3,length(EbNo));
% Set up a figure for visualizing BER results fig = figure; grid on; ax = fig.CurrentAxes; hold(ax,'on'); ax.YScale = 'log'; xlim(ax,[EbNo(1), EbNo(end)]); ylim(ax,[1e-4 1]); xlabel(ax,'Eb/No (dB)'); ylabel(ax,'BER'); fig.NumberTitle = 'off'; fig.Name = 'Orthogonal Space-Time Block Coding'; fig.Renderer = 'zbuffer'; title(ax,'Alamouti-coded 2x2 System'); set(fig,'DefaultLegendAutoUpdate','off'); fig.Position = figposition([41 50 25 30]); % Loop over several EbNo points for idx = 1:length(EbNo) reset(errorCalc1); reset(errorCalc2); % Loop till the number of errors exceed 'maxNumErrs' % or the maximum number of packets have been simulated while (ber_Estimate(2,idx) < maxNumErrs) && ... (ber_Known(2,idx) < maxNumErrs) && ... (ber_Estimate(3,idx)/frmLen < maxNumPackets) % Generate data vector per frame data = randi([0 P-1], frmLen, 1); % Modulate data modData = pskmod(data,P); % Alamouti Space-Time Block Encoder encData = ostbcEnc(modData); % Prepend pilot symbols for each frame txSig = [pilots; encData]; % Pass through the 2x2 channel reset(chan); [chanOut, H] = chan(txSig); % Add AWGN rxSig = awgn(chanOut,SNR(idx)); % Channel Estimation % For each link => N*M estimates HEst(1,:,:) = pilots(:,:).' * rxSig(1:pLen, :) / pLen; % assume held constant for the whole frame HEst = HEst(ones(frmLen, 1), :, :); % Combiner using estimated channel decDataEst = ostbcComb(rxSig(pLen+1:end,:), HEst); % Combiner using known channel decDataKnown = ostbcComb(rxSig(pLen+1:end,:), ... squeeze(H(pLen+1:end,:,:,:))); % ML Detector (minimum Euclidean distance) demodEst = pskdemod(decDataEst,P); % estimated demodKnown = pskdemod(decDataKnown,P); % known % Calculate and update BER for current EbNo value % for estimated channel ber_Estimate(:,idx) = errorCalc1(data, demodEst); % for known channel ber_Known(:,idx) = errorCalc2(data, demodKnown); end % end of FOR loop for numPackets % Plot results semilogy(ax,EbNo(1:idx), ber_Estimate(1,1:idx), 'ro'); semilogy(ax,EbNo(1:idx), ber_Known(1,1:idx), 'g*'); legend(ax,['Channel estimated with ' num2str(pLen) ' pilot symbols/frame'],... 'Known channel'); drawnow; end % end of for loop for EbNo % Perform curve fitting and replot the results fitBEREst = berfit(EbNo, ber_Estimate(1,:)); fitBERKnown = berfit(EbNo, ber_Known(1,:)); semilogy(ax,EbNo, fitBEREst, 'r', EbNo, fitBERKnown, 'g'); hold(ax,'off'); % Restore default stream rng(s)
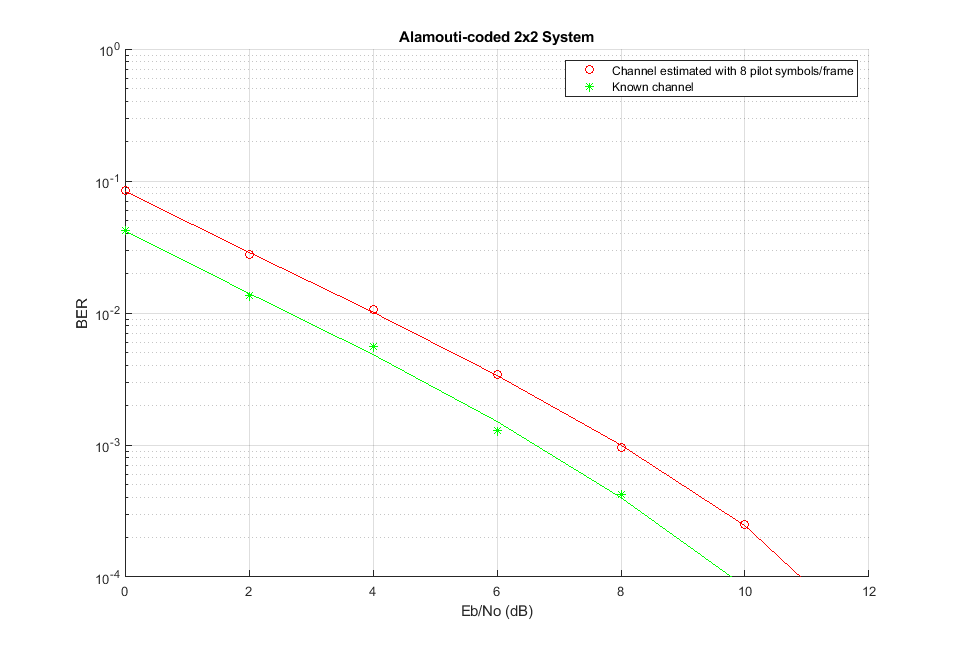
シミュレートした 2x2 システムのダイバーシティ次数は、前の節の 1x2 システムおよび 2x1 システムで認められたダイバーシティ次数とは異なります。
データの 100 個のシンボルごとに 8 個のパイロット シンボルがあるため、選択した Eb/No 範囲における特性がチャネル推定により約 1 dB 低下することに注目してください。これは、フレームあたりのパイロット シンボル数を増やすと改善されますが、リンクのオーバーヘッドが増大します。この比較では、シンボルあたりの送信 SNR を両方のケースで同じ値に維持します。
付属の関数スクリプト ostbc2m_e.m は、関心のあるユーザーがさらに実験するうえで役立ちます。
パート 3: 直交時空間ブロック符号化 (OSTBC) とその他の調査
この最後の節では、[ 4 ] に従い、ハーフレート コード G4 を使用する 4 つの送信アンテナ (4x1 システム) を使用する直交空間時間ブロック符号化の実行結果をいくつか示します。
ダイバーシティ次数は 4 になると予想され、この値を 1x4 と 2x2 の各システムと比較します。これらのシステムでもダイバーシティ次数は同じです。公平に比較するため、ハーフレート G4 コードのある 4 位相 PSK を使用して、同じ伝送速度 1 ビット/秒/Hz を達成します。
これらの結果を単一コア上で得るには時間がしばらくかかります。Parallel Computing Toolbox™ (PCT) をインストールしていない場合、先行シミュレーションの結果を読み込みます。関数スクリプト ostbc4m.m を組み込みます。これは、これらの結果を得るために mrc1m.m および ostbc2m.m とともに使用された関数スクリプトです。PCT がインストールされている場合、これらのシミュレーションは並行で実行されます。この場合、関数スクリプト ostbc4m_pct.m、mrc1m_pct.m および ostbc2m_pct.m が使用されます。他のコードとシステムを検討するために、これらのスクリプトを出発点として使用するよう強くお勧めします。
[licensePCT,~] = license( 'checkout' , 'Distrib_Computing_Toolbox'); if (licensePCT && ~isempty(ver('parallel'))) EbNo = 0:2:20; [ber11, ber14, ber22, ber41] = mimoOSTBCWithPCT(100,4e3,EbNo); else load ostbcRes.mat; end % Set up a figure for visualizing BER results fig = figure; grid on; ax = fig.CurrentAxes; hold(ax,'on'); fig.Renderer = 'zbuffer'; ax.YScale = 'log'; xlim(ax,[EbNo(1), EbNo(end)]); ylim(ax,[1e-5 1]); xlabel(ax,'Eb/No (dB)'); ylabel(ax,'BER'); fig.NumberTitle = 'off'; fig.Name = 'Orthogonal Space-Time Block Coding(2)'; title(ax,'G4-coded 4x1 System and Other Comparisons'); set(fig,'DefaultLegendAutoUpdate','off'); fig.Position = figposition([30 15 25 30]); % Theoretical performance of fourth-order diversity for QPSK BERthy4 = berfading(EbNo, 'psk', 4, 4); % Plot results semilogy(ax,EbNo, ber11, 'r*', EbNo, ber41, 'ms', EbNo, ber22, 'c^', ... EbNo, ber14, 'ko', EbNo, BERthy4, 'g'); legend(ax,'No Diversity (1Tx, 1Rx), BPSK', 'OSTBC (4Tx, 1Rx), QPSK', ... 'Alamouti (2Tx, 2Rx), BPSK', 'Maximal-Ratio Combining (1Tx, 4Rx), BPSK', ... 'Theoretical 4th-Order Diversity, QPSK'); % Perform curve fitting on non-zero BER points lenBER11 = length(ber11(ber11~=0)); lenBER41 = length(ber41(ber41~=0)); lenBER22 = length(ber22(ber22~=0)); lenBER14 = length(ber14(ber14~=0)); fitBER11 = berfit(EbNo(1:lenBER11), ber11(1:lenBER11)); fitBER41 = berfit(EbNo(1:lenBER41), ber41(1:lenBER41)); fitBER22 = berfit(EbNo(1:lenBER22), ber22(1:lenBER22)); fitBER14 = berfit(EbNo(1:lenBER14), ber14(1:lenBER14)); semilogy(ax,EbNo(1:lenBER11), fitBER11, 'r', EbNo(1:lenBER41), fitBER41, 'm', ... EbNo(1:lenBER22), fitBER22, 'c', EbNo(1:lenBER14), fitBER14, 'k'); hold(ax,'off');
Starting parallel pool (parpool) using the 'Processes' profile ... Connected to parallel pool with 8 workers.
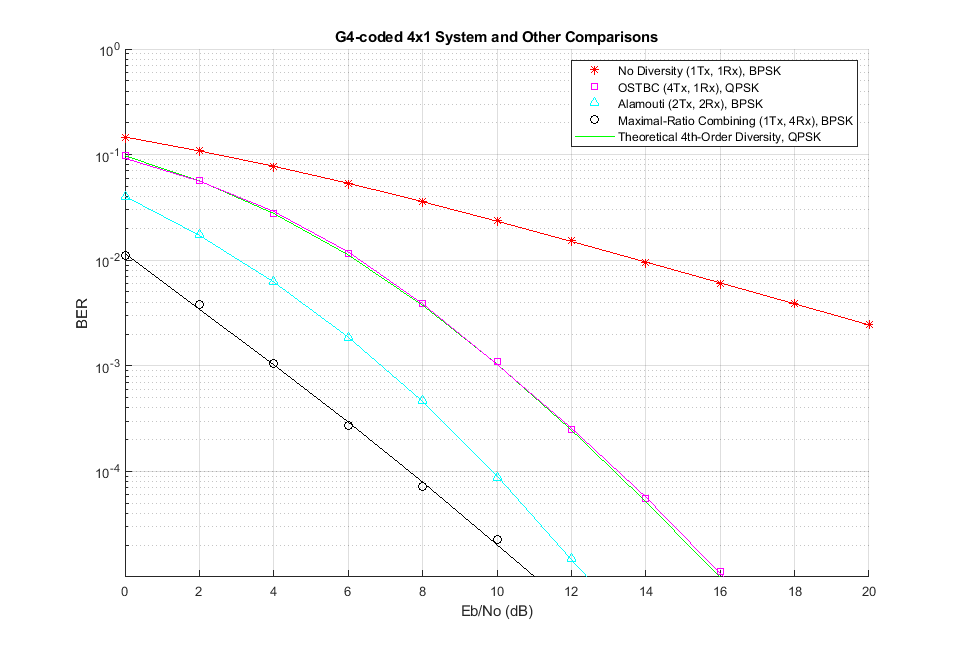
予想どおり、4x1、2x2、および 1x4 の各システムで BER 曲線の傾きはほぼ同じになりますが、これは各システムのダイバーシティ次数が同じであることを示します。
また、4x1 システムでは 3 dB のペナルティが認められますが、これは、これら 3 つのシステムの総送信電力が同じ値であると仮定されていることが原因であると考えられます。これら 3 つのシステムの受信電力が同じになるように送信電力を較正すると、3 つのシステムの特性は同じになります。今回も、理論上の特性は 4x1 システムのシミュレーション特性と一致します。これは、ダイバーシティ分枝で総電力が正規化されるからです。
付録
この例では、以下の補助関数を使用します。
参考文献
S. M. Alamouti, "A simple transmit diversity technique for wireless communications", IEEE® Journal on Selected Areas in Communications, Vol. 16, No. 8, Oct. 1998, pp. 1451-1458.
V. Tarokh, H. Jafarkhami, and A.R. Calderbank, "Space-time block codes from orthogonal designs", IEEE Transactions on Information Theory, Vol. 45, No. 5, Jul. 1999, pp. 1456-1467.
A.F. Naguib, V. Tarokh, N. Seshadri, and A.R. Calderbank, "Space-time codes for high data rate wireless communication: Mismatch analysis", Proceedings of IEEE International Conf. on Communications, pp. 309-313, June 1997.
V. Tarokh, H. Jafarkhami, and A.R. Calderbank, "Space-time block codes for wireless communications: Performance results", IEEE Journal on Selected Areas in Communications, Vol. 17, No. 3, Mar. 1999, pp. 451-460.
